Instability Evolution of Single Fracture with Different Dip Angles on Heterogeneous Rock
-
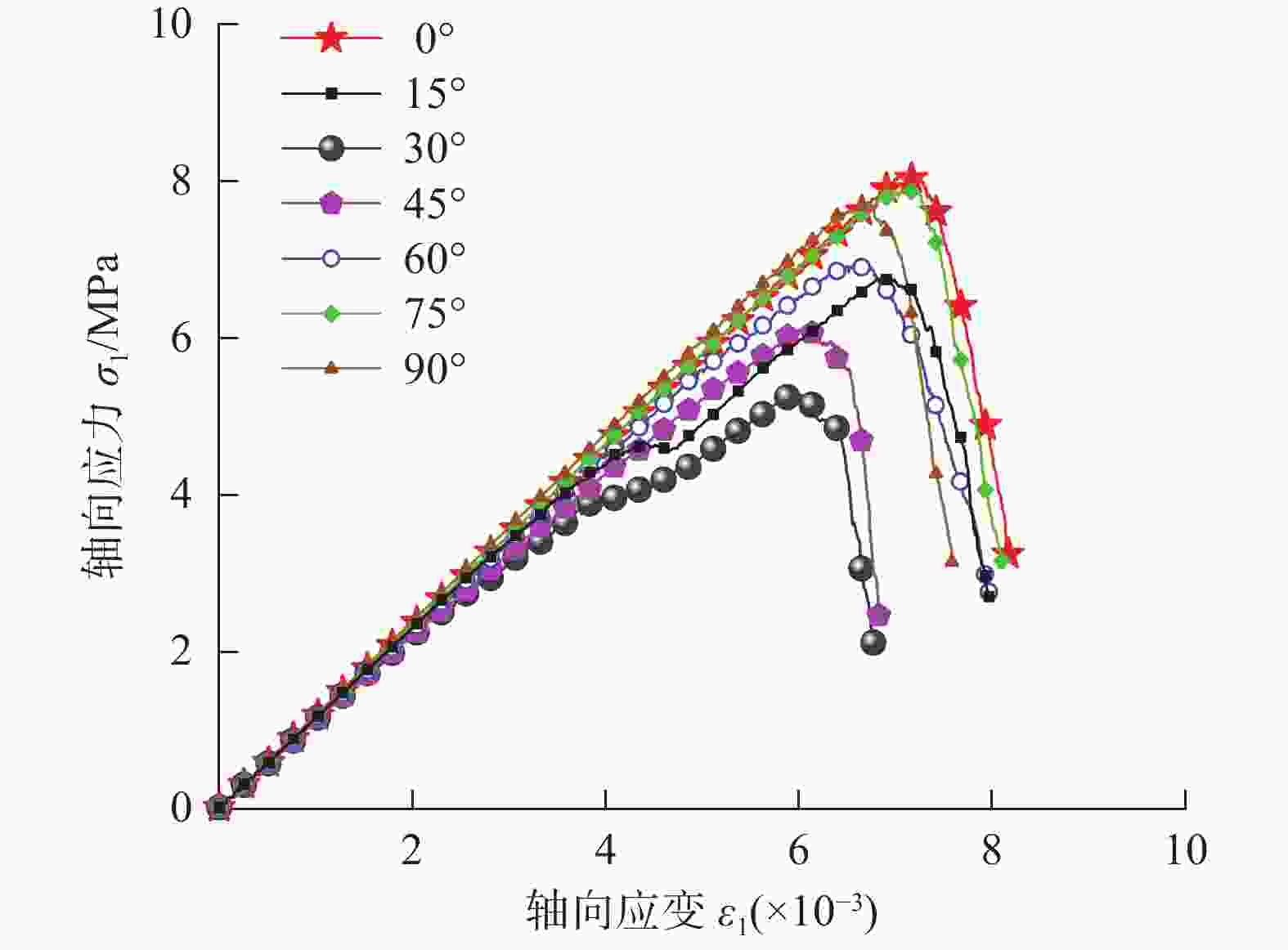
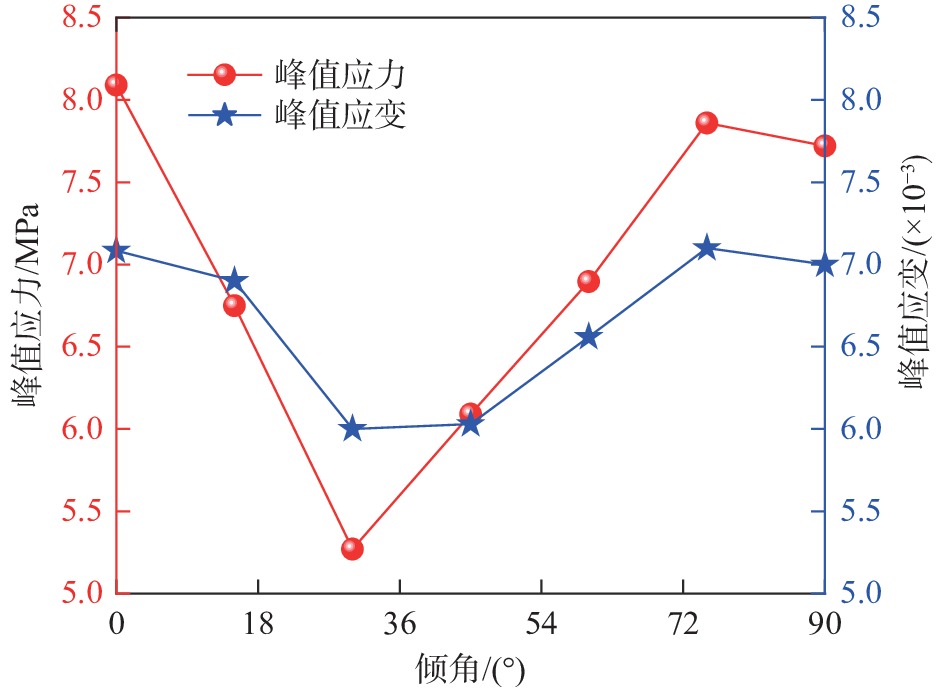
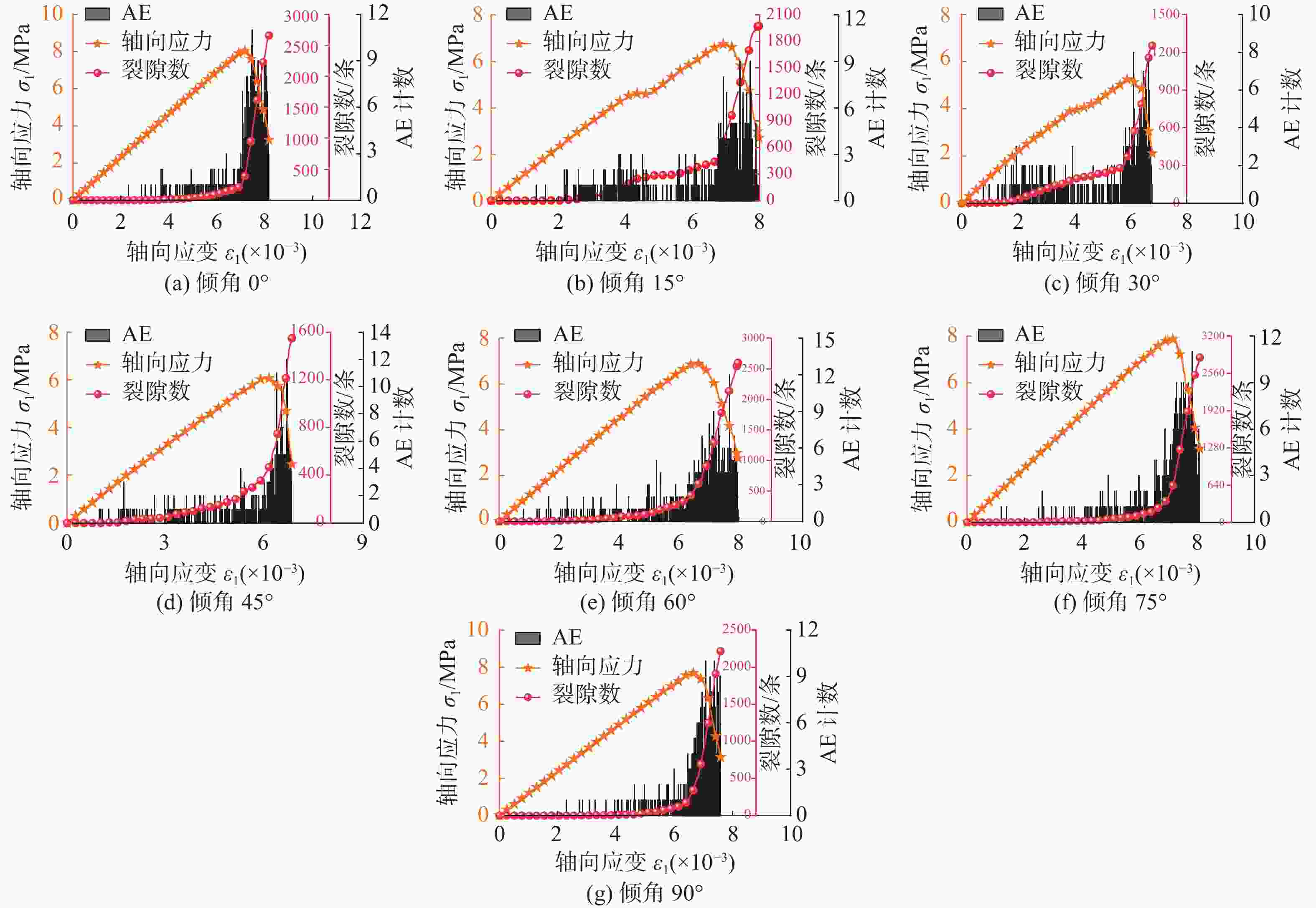
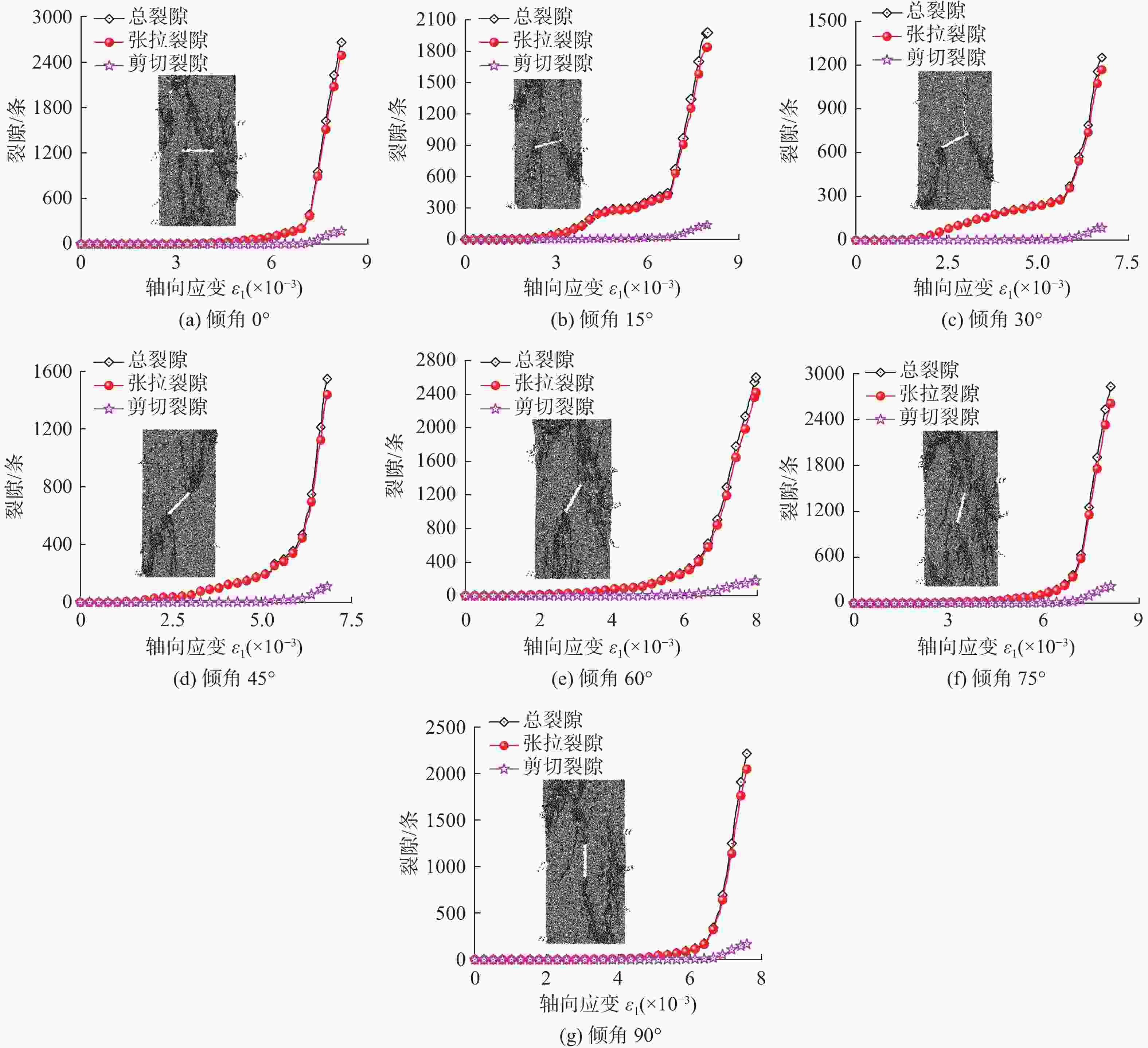
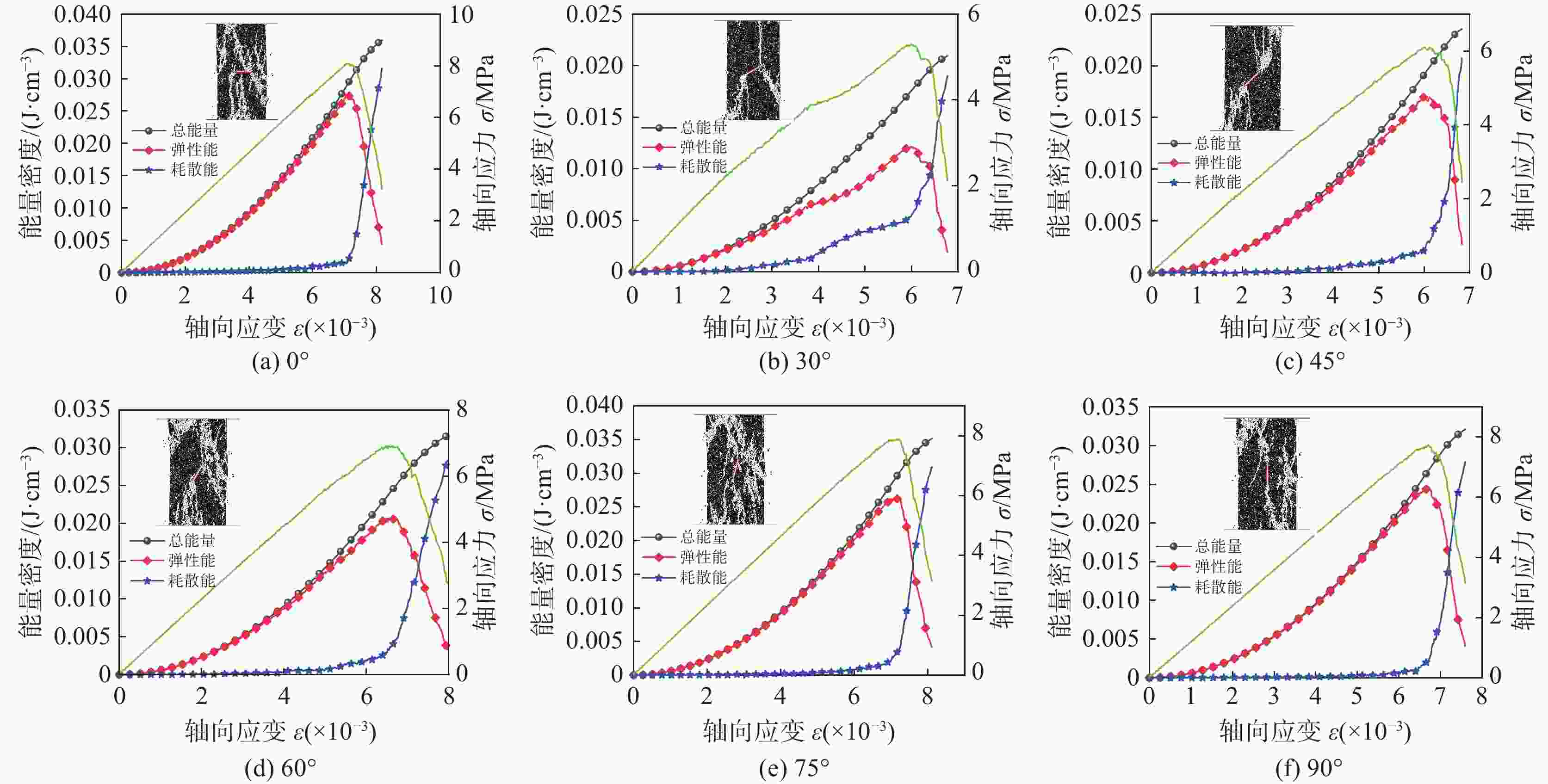
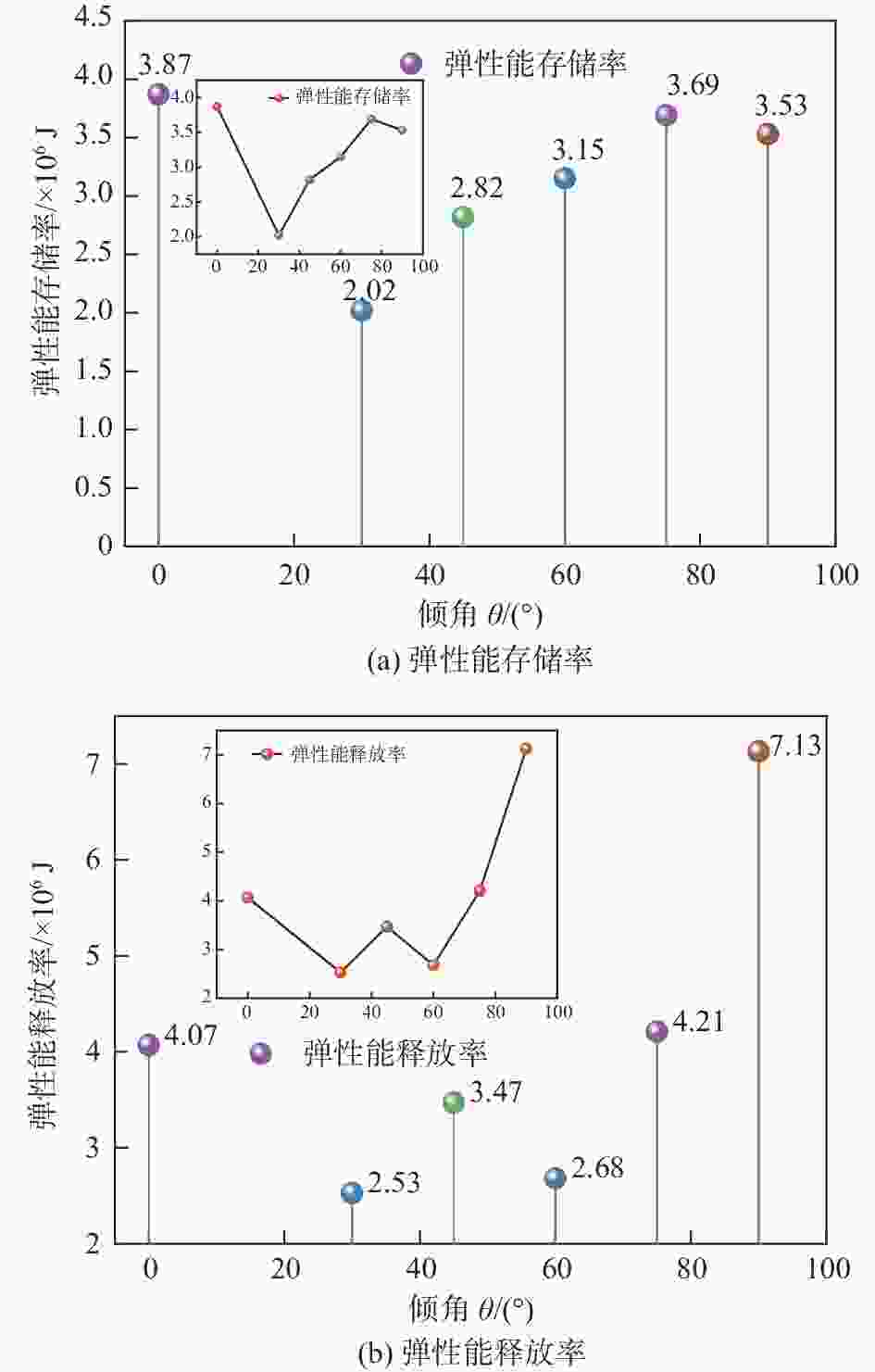
摘要: 岩体中的裂隙对岩石的力学行为、能量演化和失稳破坏有显著影响。为阐明不同倾角单裂隙对岩石能量演化和失稳破坏机理,基于颗粒流PFC2D方法,建立了不同倾角单裂隙砂质泥岩数值模型,模拟了不同倾角单裂隙下砂质泥岩的单轴压缩试验。研究表明,随着单裂隙倾角变大,砂质泥岩的强度与弹性模量先降低后增大,预制裂纹会影响断裂面的裂纹起始位置,并加速断裂面的形成;声发射事件在岩样破坏前存在小范围沉寂期,该特征可作为岩石破坏的前兆判据;随着裂隙倾角的增大,总能量持续增大,弹性能和耗散能呈现先增加后减小的趋势,倾角30°时,岩石试样冲击倾向性最弱,有利于降低冲击地压危险,倾角为90°时,岩石试样冲击倾向性相对最强,不利于冲击地压的防治。Abstract: Fractures in rock mass have a significant influence on the mechanical behavior, energy evolution and instability failure of rock. To clarify the rock energy evolution and instability failure mechanism of single fracture with different dip angles, based on the particle flow PFC2D method, a numerical model of sandy mudstone with single fracture with different dip angles was established, and the uniaxial compression test of sandy mudstone with single fracture with different dip angles was simulated. The results show that with the increase of single fracture dip angle, the strength and elastic modulus of sandy mudstone decrease first and then increase, and the prefabricated crack will affect the crack initiation position of the fracture surface and accelerate the formation of the fracture surface. The acoustic emission event has a small range of quiet period before the rock sample is destroyed, which can be used as a precursory criterion for rock failure. With the increase of fracture dip angle, the total energy continues to increase, and the elastic energy and dissipation energy show a trend of increasing first and then decreasing. When the dip angle is 30°, the rock sample has the weakest impact tendency, which is beneficial to reduce the risk of rock burst. When the dip angle is 90°, the rock sample has the strongest impact tendency, which is not conducive to the prevention and control of rock burst.
-
Key words:
- PFC2D /
- rock /
- single fracture dip angle /
- AE /
- energy evolution /
- elastic energy storage rate /
- elastic energy releasing rate
-
表 1 模型初始物理属性
颗粒粒径/mm 密度/(kg·m-3) 孔隙比 颗粒数n Rmax/mm 0.4~0.6 2620 0.1 5657 0.6 表 2 数值模型细观参数
模型参数 符号 取值 密度/(kg·m-3) $ \rho $ 2620 孔隙度 $ \varphi $ 0.1 颗粒最大粒径/mm $ {R}_{\max } $ 0.6 颗粒粒径比 $ R_{\text {max }} / R_{\min } $ 1.5 弹性模量/GPa E* 0.535 刚度比 k* 1.5 摩擦系数 $ {\mu} $ 0.32 平行黏结有效模量/GPa $ \bar{E}^* $ 11.5 平行黏结刚度比 $ \bar{k}^{*} $ 1.5 法向黏结强度/MPa $ \bar{\sigma}_{c} $ 2.0 切向黏结强度/MPa $ \bar{c} $ 2.71 摩擦角/(°) $ \bar{\phi} $ 40 表 3 数值模型细观参数
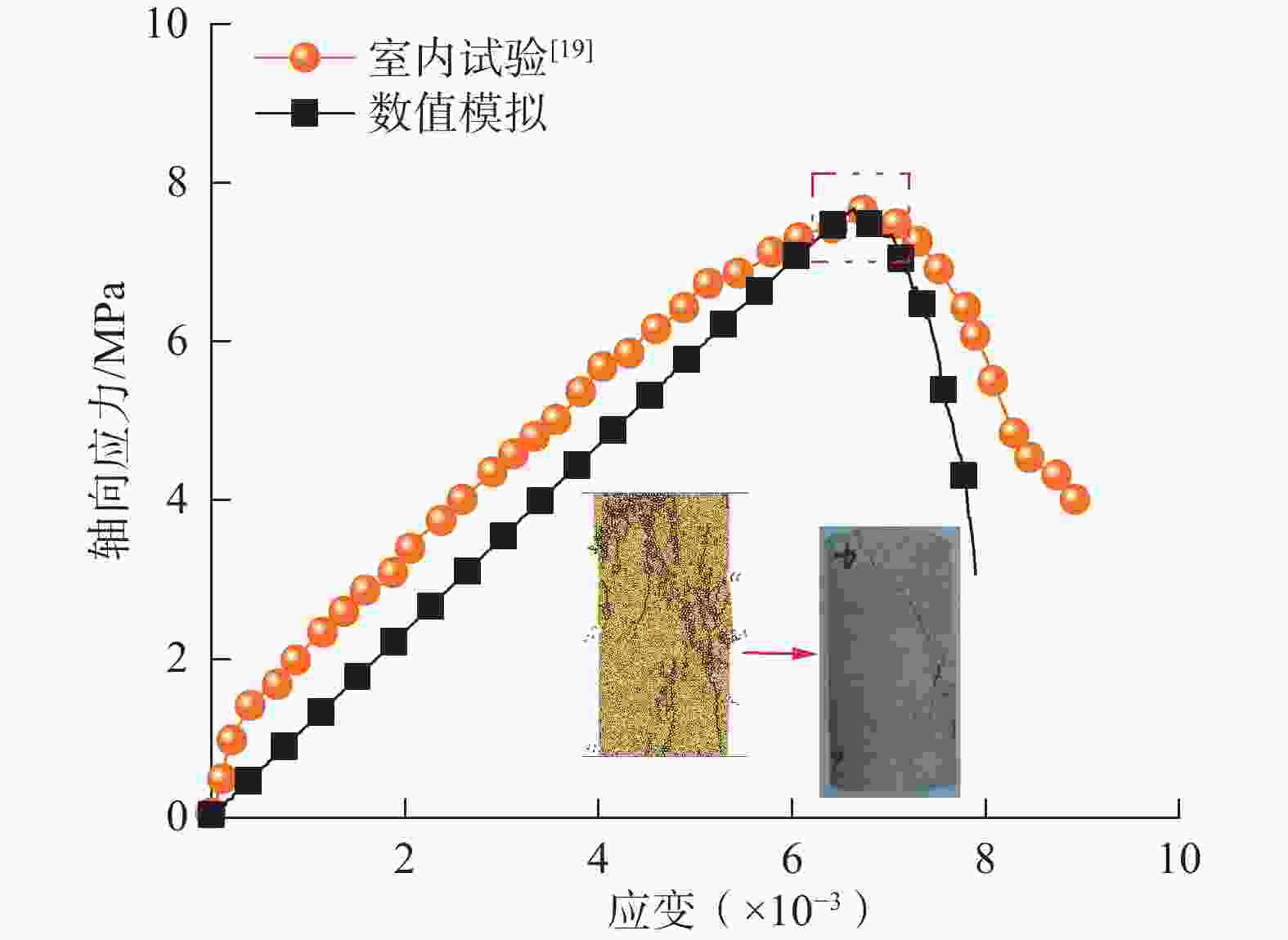
峰值应力/MPa 峰值应变(×10−3) 弹性模量/GPa 文献试验[19] 7.48 6.40 1.163 数值模拟值 7.65 6.63 1.154 误差 2% 3% 0.7% -
[1] 王春萍, 王 璐, 刘建锋, 等. 单轴压缩条件下单裂隙花岗岩力学特性及破坏特征[J]. 西南交通大学学报,2024,59(2):369-376, 446. [2] 钟 振, 孟 醒, 胡云进, 等. 考虑基质渗透性的岩体单裂隙渗流及影响因素的室内和数值试验研究[J]. 岩石力学与工程学报,2023,42(9):2148-2163. [3] 宋 洋, 罗志恒, 张 波, 等. 裂隙位置对类岩体短柱单轴压缩破坏形态影响[J]. 山东大学学报(工学版),2023,53(5):121-131. [4] 宋勇军, 李晨婧, 毕 冉, 等. 冻融作用下岩石孔隙扩展演化特征研究[J]. 冰川冻土,2023,45(3):1116-1127. [5] 陈家嵘, 周昌台, 周 韬, 等. 压剪荷载下含单一裂隙砂岩的应变演化与破坏特征研究[J]. 岩石力学与工程学报,2023,42(7):1743-1758. [6] 王 磊, 刘化强, 李少波, 等. 不同围压下含预制裂隙煤体裂隙演化特征研究[J]. 采矿与安全工程学报,2023,40(4):786-797. [7] 王 磊, 刘化强, 李少波, 等. 煤体张开型裂隙演化规律及失稳前兆试验[J].中国矿业大学学报,2024,53(2):250-263. [8] LI X, YAO Z, LIU X, HUANG X. Energy evolution and damage mechanism of fractured sandstone with different angles. Energies. 2022, 15(4): 1518. [9] CHEN J, YIN X, ZHOU C, et al. Interaction between flaws and failure characteristics of red sandstone containing double flaws under compressive-shear loading[J]. Engineering Fracture Mechanics, 2023, 292, 109664. [10] 章德超, 肖桃李, 折海成, 等. 基于DIC的裂隙分布对层状复合岩力学特性及变形破坏影响研究[J/OL]. 中国测试, 2023, 1-11. http://kns.cnki.net/kcms/detail/51.1714.TB.20230928.1719.002.html. [11] 周春煦, 冯红春, 周文正. 充填双裂隙砂岩力学特性及裂隙演化规律研究[J/OL].有色金属科学与工程, 2024, 1-13. http://kns.cnki.net/kcms/detail/36.1311.TF.20231013.1607.004.html. [12] ZHANG Y, ZHONG L, PANG F, et al. Characteristics of energy dissipation in T-shaped fractured rocks under different loading rates[J]. Sustainability,2023,15(18):13695. doi: 10.3390/su151813695 [13] CHEN Y, TANG Y, CAO R, et al. Failure mode of parallel-fractured rock-like sample with different inclinations[J]. Theoretical and Applied Fracture Mechanics,2023,127:104053. doi: 10.1016/j.tafmec.2023.104053 [14] REN X, ZHANG H, ZHANG J, et al. Numerical simulation analysis of fracture propagation in rock based on smooth particle hydrodynamics[J]. Materials,2023,16(19):6560. doi: 10.3390/ma16196560 [15] 张 岩, 经 纬, 经来旺, 等. 裂隙倾角及长度对岩石强度和破坏特征影响数值模拟[J]. 煤炭技术,2023,42(10):106-109. [16] 王子航, 陈俊智, 冯豪天. 直剪条件下含裂隙岩石变形特征研究[J]. 有色金属(矿山部分),2023,75(5):127-133. [17] WU Y, MA D, HU X, et al. Numerical simulation on the mechanical and fracture behavior of bedding argillaceous sandstone containing two pre-existing flaws[J]. Theoretical and Applied Fracture Mechanics,2023,127:104047. doi: 10.1016/j.tafmec.2023.104047 [18] 李志强, 刘国锋, 晏长根, 等. 含原生隐微裂隙岩石颗粒流模型构建及细观参数标定方法研究[J].工程地质学报,2023,31(6):1842-1853. [19] 石 崇, 张 强, 王盛年. 颗粒流(PFC5.0)数值模拟技术及应用[J]. 岩土力学,2018,39(S2):36. [20] 原先凡. 砂质泥岩卸荷流变力学特性研究[D]. 宜昌: 三峡大学, 2014. [21] ZHANG S, CHEN L, LU P, et al. Analysis of the energy and damage evolution rule for sandstone based on the particle flow method[J]. Mechanics of Time-Dependent Materials,2022,26(3):531-546. doi: 10.1007/s11043-021-09499-9 [22] YANG Y S, CHENG W, ZHANG Z R, et al. Energy evolution law of marble failure process under different confining pressures based on particle discrete element method[J]. Frontiers in Materials,2021,8:665955. doi: 10.3389/fmats.2021.665955 [23] 王桂林, 张 亮, 许 明, 等. 单轴压缩下非贯通节理岩体损伤破坏能量演化机制研究[J]. 岩土工程学报,2019,41(4):639-647. doi: 10.11779/CJGE201904006 [24] 刘鹏飞, 范俊奇, 郭佳奇, 等. 三轴应力下花岗岩加载破坏的能量演化和损伤特征[J]. 高压物理学报,2021,35(2):44-53. [25] 尹升华, 侯永强, 杨世兴, 等. 单轴压缩下混合集料胶结充填体变形破坏及能耗特征分析[J]. 中南大学学报(自然科学版),2021,52(3):936-947. [26] LI P, CAI M. Energy evolution mechanism and failure criteria of jointed surrounding rock under uniaxial compression[J]. Journal of Central South University,2021,28(6):1857-1874. doi: 10.1007/s11771-021-4735-5 [27] 张如九, 张延杰, 高 仝, 等. 基于最大能量耗散率的岩爆倾向性指标研究[J].岩石力学与工程学报,2023,42(12):2993-3009. [28] 张 亮, 王桂林, 雷瑞德, 等. 单轴压缩下不同长度单裂隙岩体能量损伤演化机制[J]. 中国公路学报,2021,34(1):24-34. doi: 10.3969/j.issn.1001-7372.2021.01.003 [29] 朱志洁, 李瑞琪, 汤国水, 等. 含裂隙煤体能量耗散特征与冲击倾向性研究[J]. 煤炭科学技术,2023,51(5):32-44. -
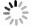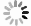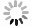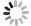




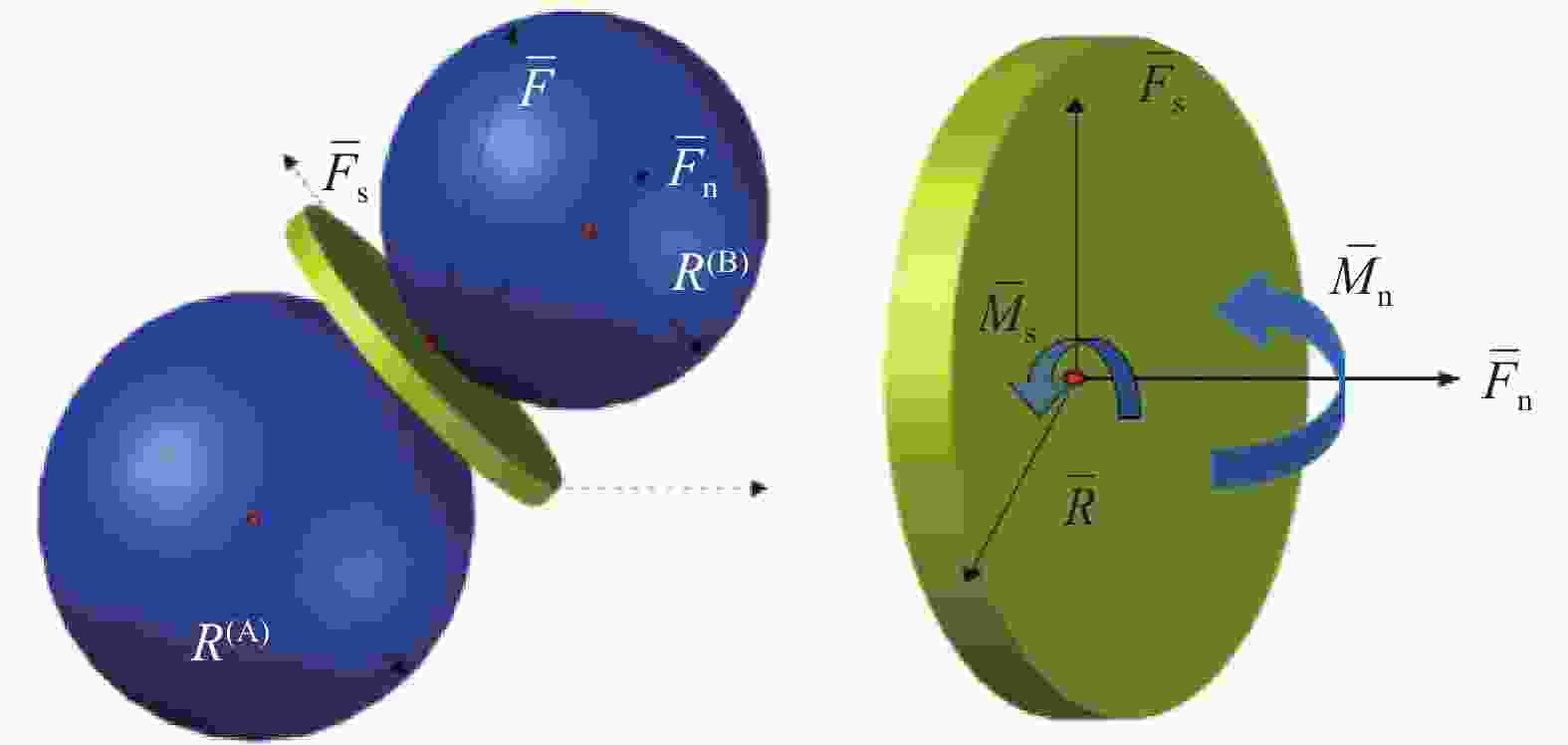
 下载:
下载: