Application of Mindlin Solution in Calculation of Ground Settlement in Composite Stratum Shield Tunnel Construction
-
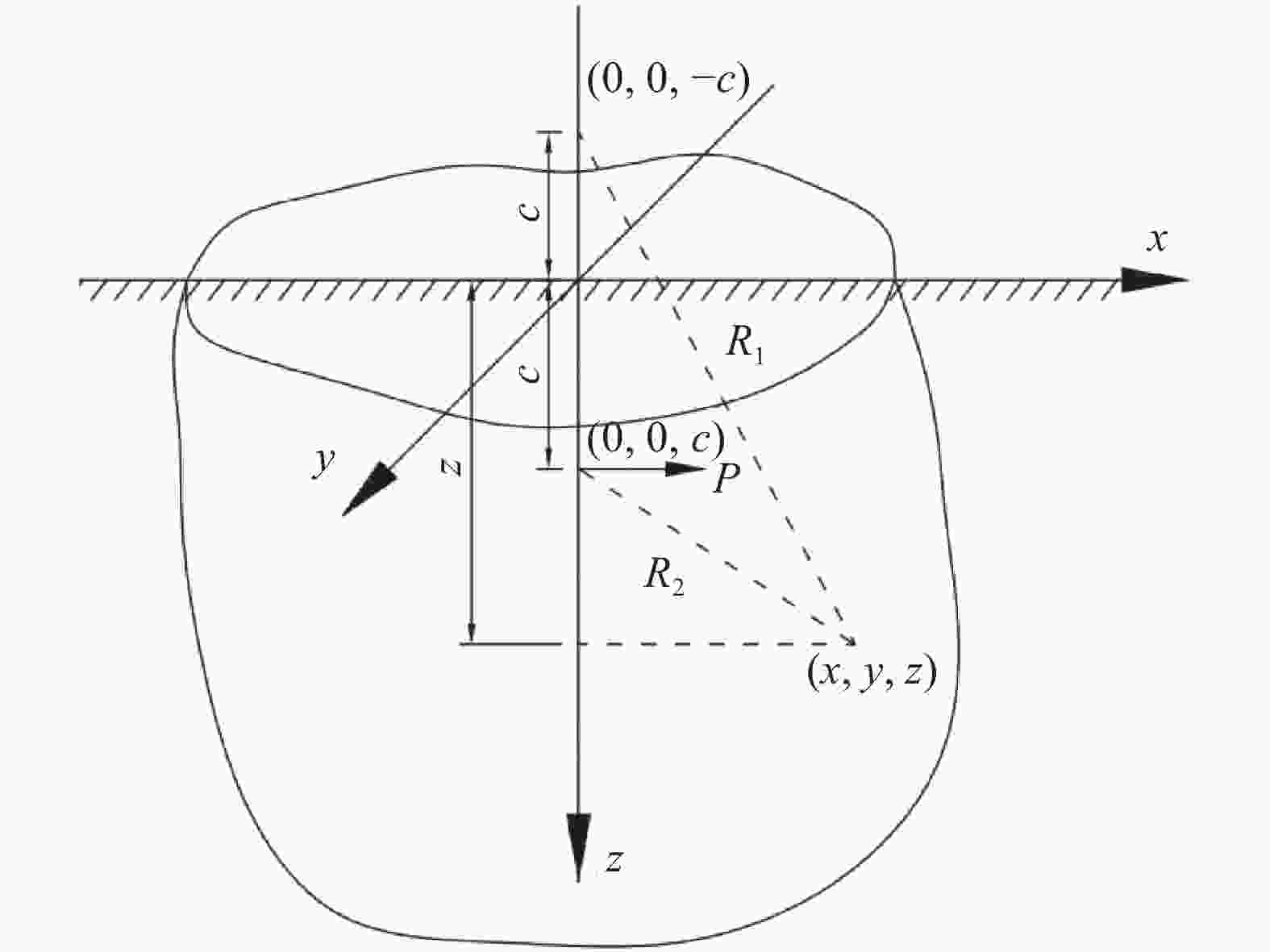
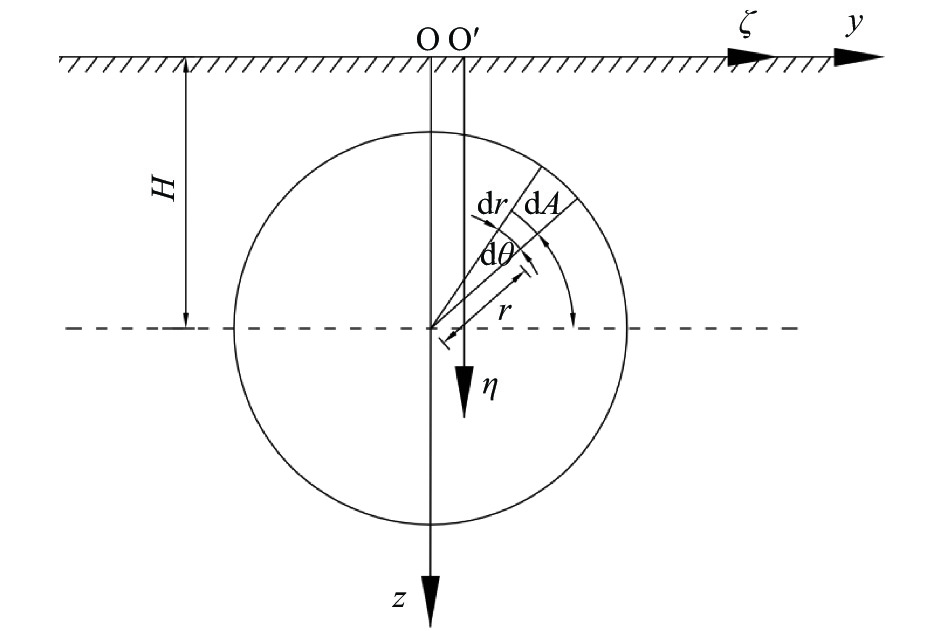
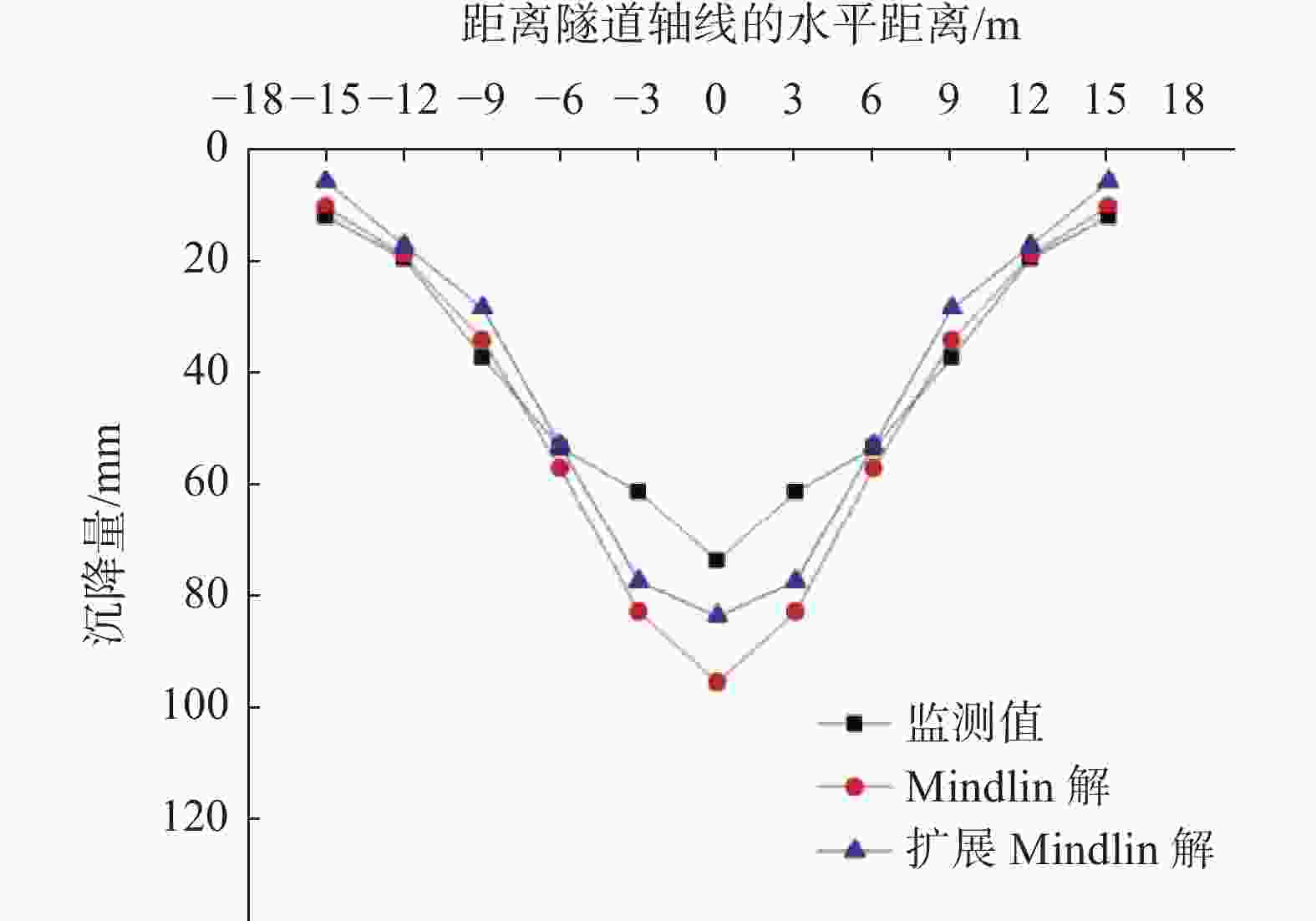
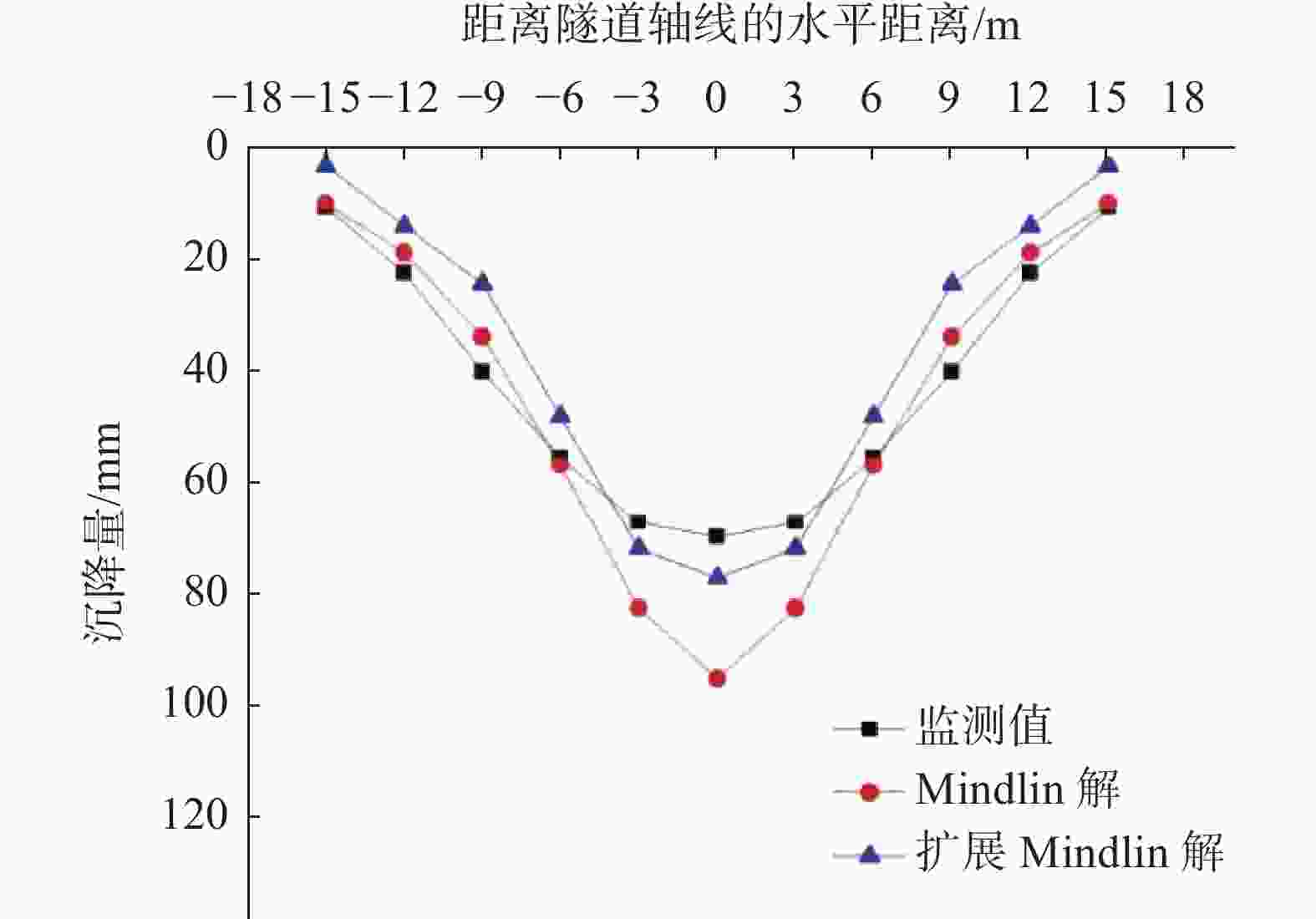
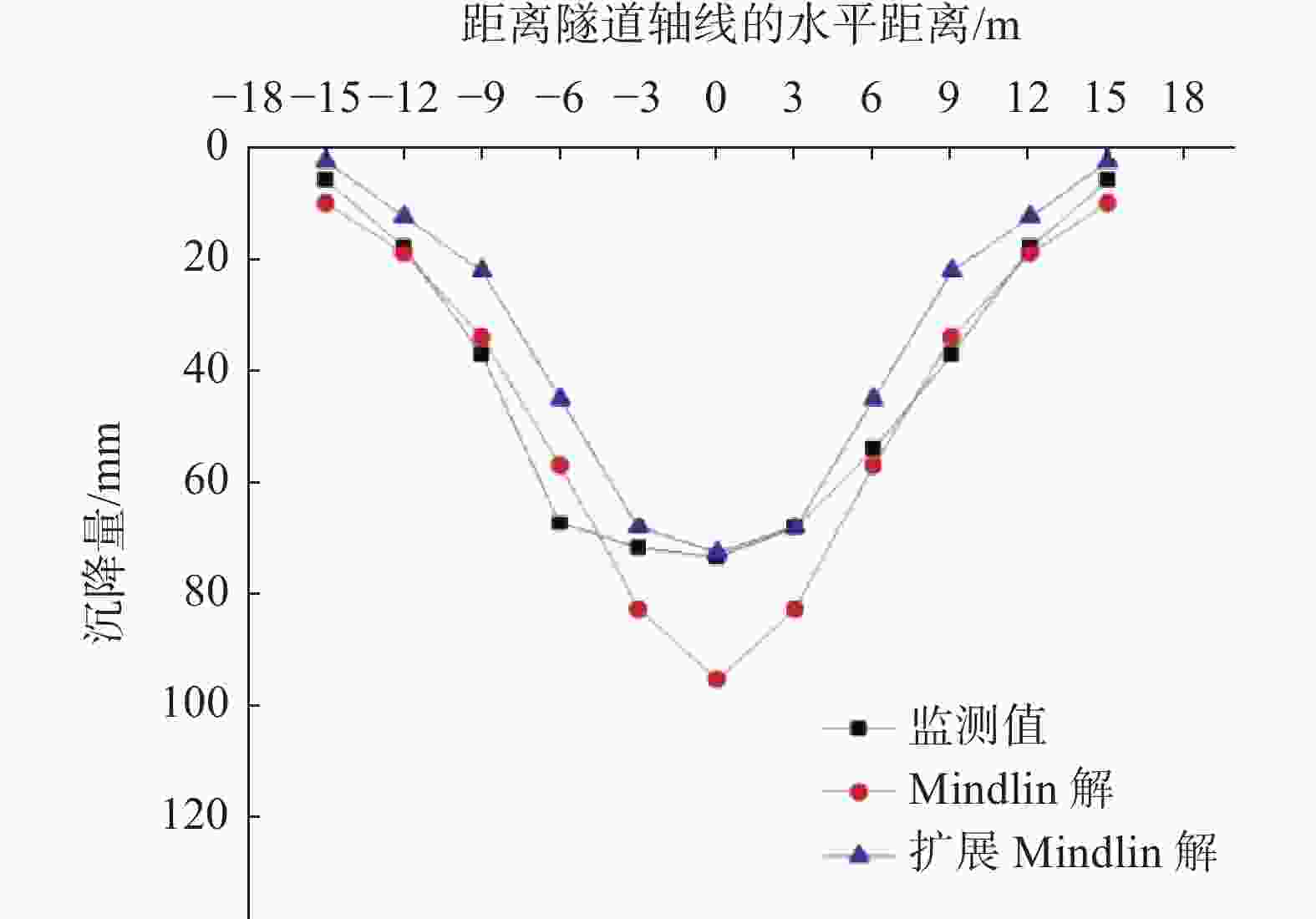
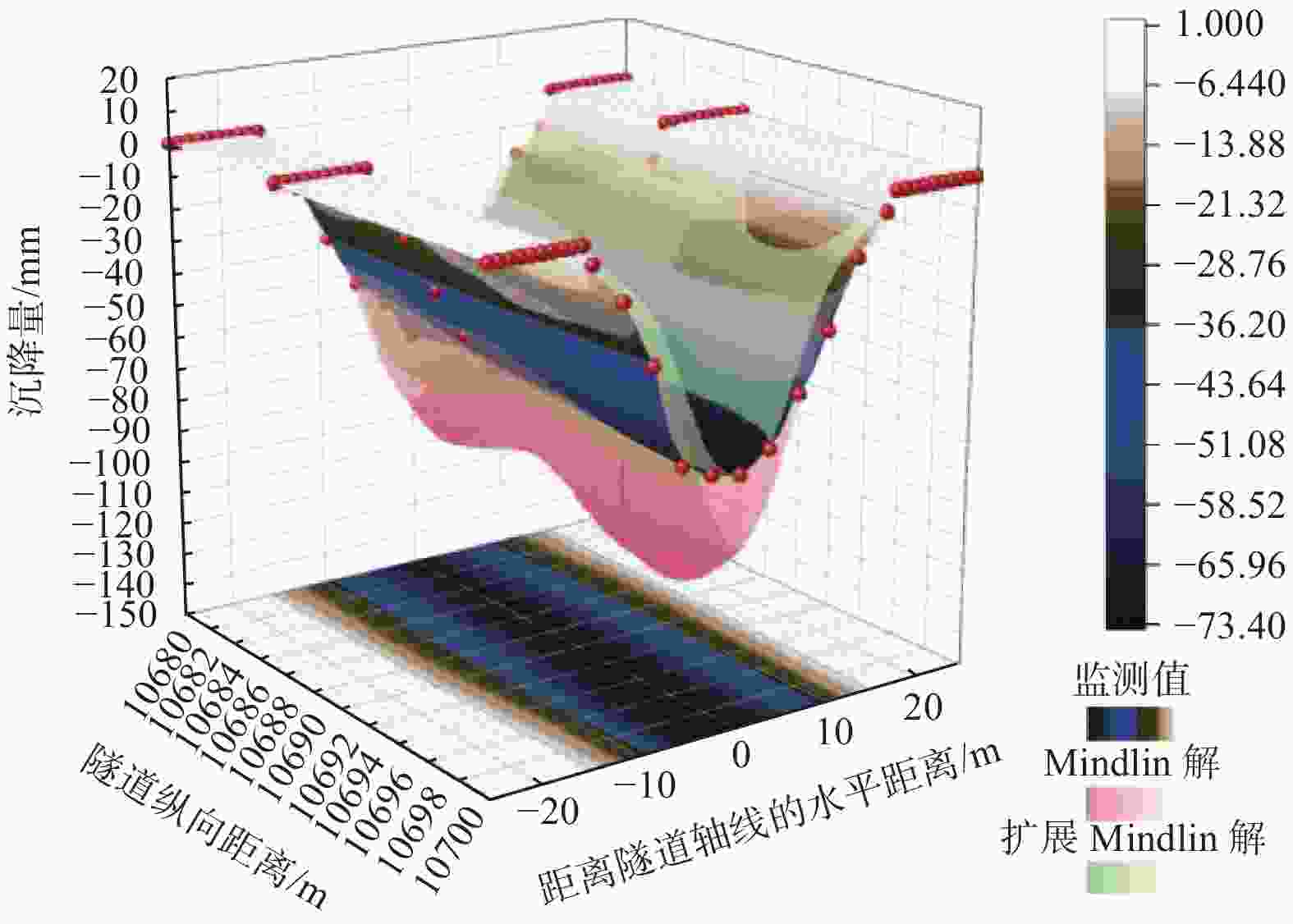
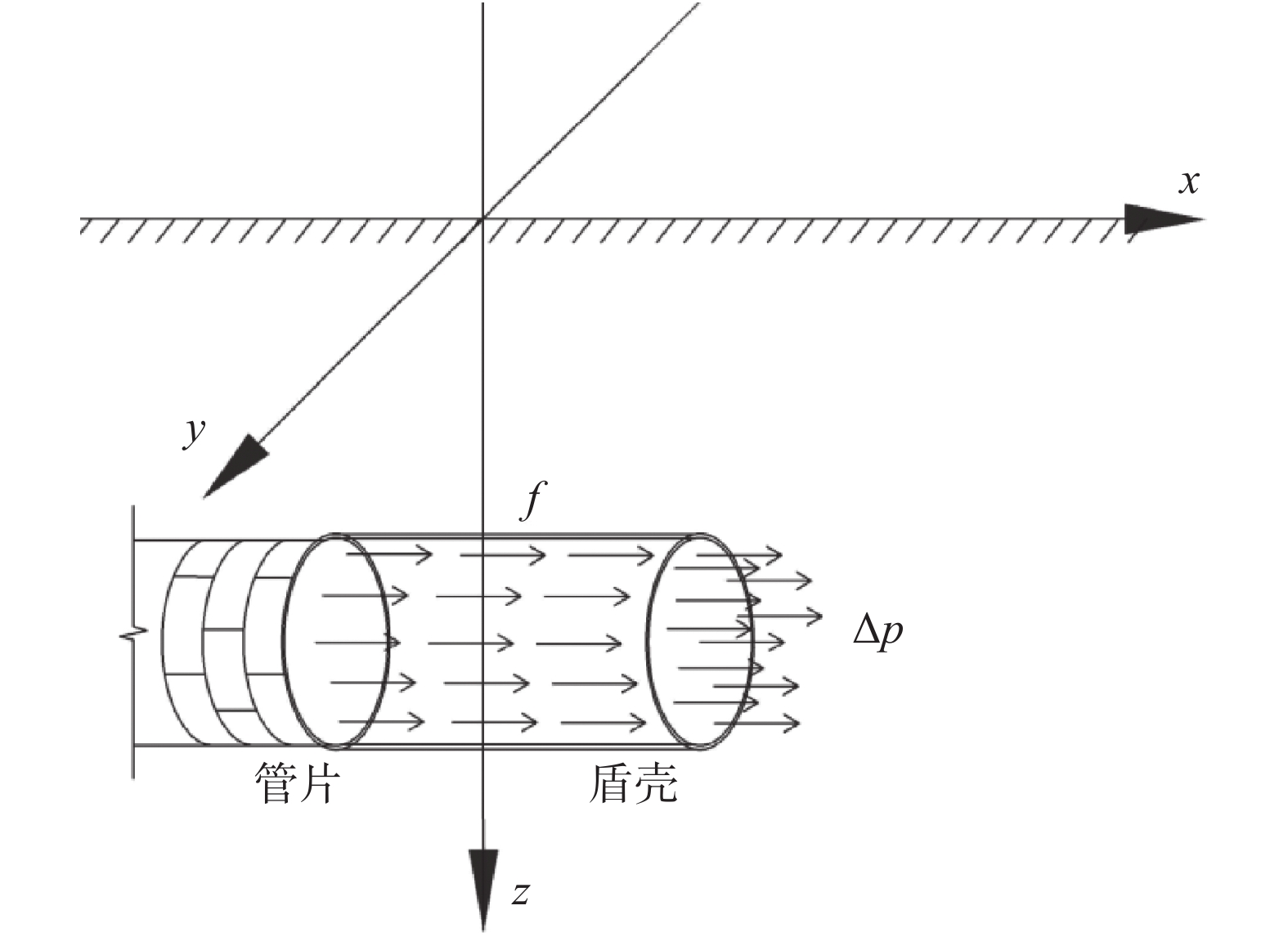
摘要: 在我国华南、东南及华北沿海地区隧道工程中,隧道围岩常为“上软下硬”的复合地层,即洞身上部是软弱的土层、下部为强度很高的硬岩地层,在该类地层中进行盾构施工引起的地面沉降问题目前还鲜见研究报道。针对此现状,延续采用Mindlin解求解地表沉降的思路,为了克服扩展Mindlin解面对非均匀地层时的局限性,引入层面状态向量,利用积分变换和矩阵推导解决了位移与应力在不同层面之间的传递问题,建立了适用于复合地层的扩展Mindlin解。对比了Mindlin解及扩展Mindlin解对复合地层中盾构隧道地表沉降问题的适应性,并与背景工程监测数据对比。推导过程表明,运用Mindlin解或扩展Mindlin解来求解地表沉降都面临困境,需要进行一定的简化。而工程监测数据则表明,采用Mindlin解计算结果偏大,可作为工程设计的参考;扩展Mindlin解计算地表沉降的方法有一定的准确性。
-
关键词:
- 上软下硬地层 /
- 地表沉降 /
- Mindlin解 /
- 扩展Mindlin解
Abstract: In the coastal areas of South China, Southeast China and North China, it is common that the upper part of the tunnel body is a soft soil layer, and the lower part is a hard rock stratum with high strength. The problem of land subsidence caused by shield tunneling has not been studied at present. To address this situation, the idea of using Mindlin solution to solve for surface subsidence was continued. In order to overcome the limitations of extended Mindlin solution for non-uniform strata, the layer state vector was introduced, and the integral transformation and matrix derivation were used to solve the relationship between displacement and stress at different layers. An extended Mindlin solution for composite formations was established. Finally, the adaptability of the Mindlin solution and the extended Mindlin solution to the surface subsidence of shield tunnels in composite strata were compared and compared with the actual engineering monitoring data. The derivation process shows that using the Mindlin solution or the extended Mindlin solution to solve the surface subsidence faces difficulties and needs to be simplified to a certain extent, while the engineering monitoring data show that the calculation results of the Mindlin solution are large, which can be used as a reference for engineering design. The method of extended Mindlin solution for calculating surface subsidence has certain accuracy. -
表 1 背景工程相关土层参数
参数类型 变形模量/
MPa泊松比 摩擦角/
(°)黏聚力/
kPa粉质黏土层 15 0.3 11.3 2 中等风化花岗岩岩层 300 0.25 45 100 表 2 科研段内不同监测断面盾构软土层厚度占比
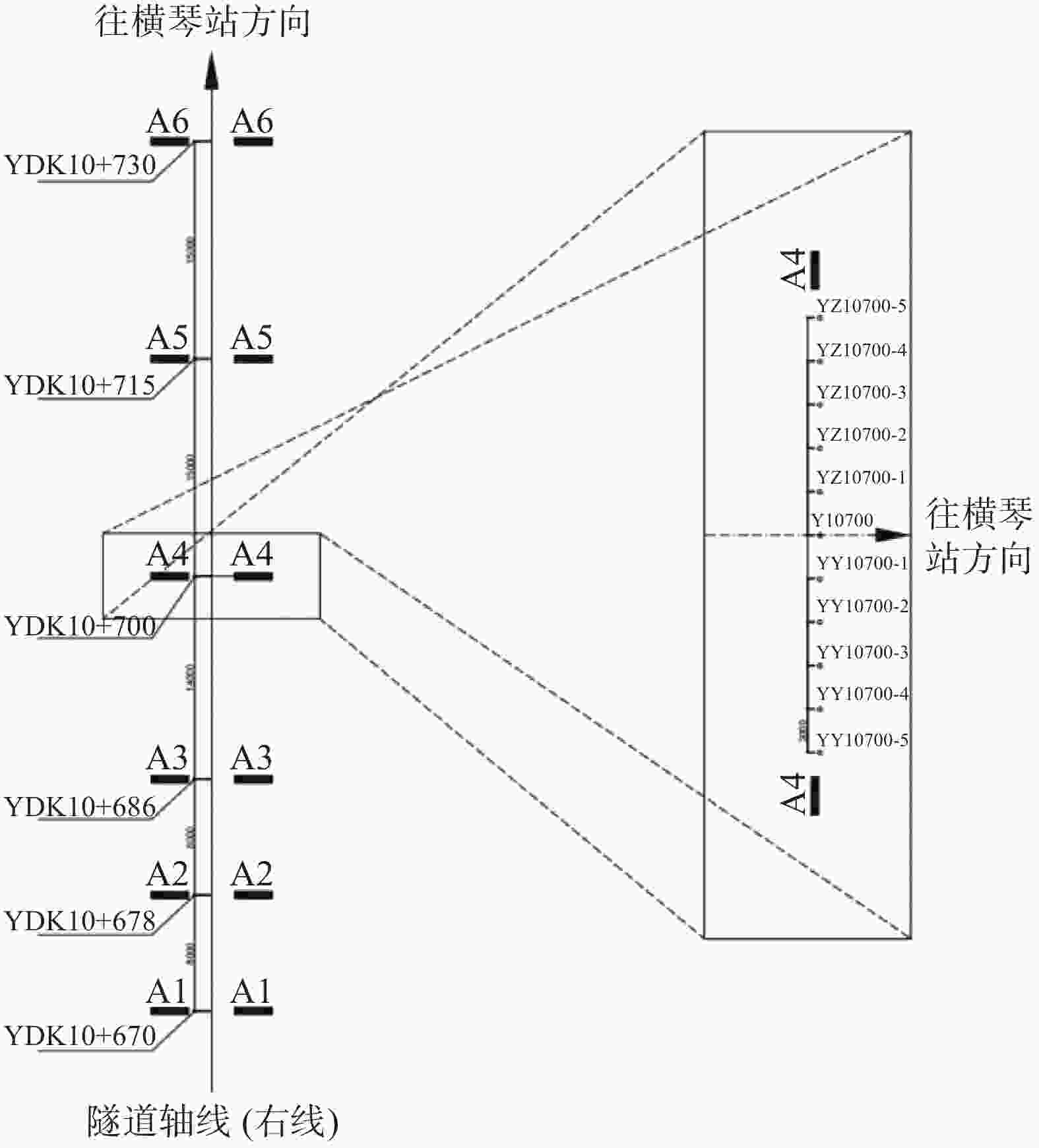
断面名称 A1-A1 A2-A2 A3-A3 A4-A4 A5-A5 A6-A6 软土层厚度占比 1/6 2/6 3/6 4/6 5/6 5/6 -
[1] 程红战,陈 健,李健斌,等. 基于随机场理论的盾构隧道地表变形分析[J]. 岩石力学与工程学报,2016,35(S2):4256-4264. doi: 10.13722/j.cnki.jrme.2016.0099 [2] 施成华,彭立敏. 随机介质理论在盾构法隧道纵向地表沉降预测中的应用[J]. 岩土力学,2004,(2):320-323. doi: 10.3969/j.issn.1000-7598.2004.02.030 [3] SAGASETA C. Analysis of undraind soil deformation due to ground loss[J]. Géotechnique,1987,37(3):301-320. [4] MINDLIN R D. Force at a point in the interior of a semi-infinite solid[J]. Physics,1936,7(5):195-202. doi: 10.1063/1.1745385 [5] 魏 纲,徐日庆. 软土隧道盾构法施工引起的纵向地面变形预测[J]. 岩土工程学报,2005,(9):1077-1081. doi: 10.3321/j.issn:1000-4548.2005.09.020 [6] SHI C H,CAO C Y,LEI M F. An analysis of the ground deformation caused by shield tunnel construction combining an elastic half-space model and stochastic medium theory[J]. Ksce Journal of Civil Engineering,2017,21(5):1933-1944. doi: 10.1007/s12205-016-0804-y [7] 金 波,唐锦春. 用积分变换及边界积分方法求解多层地基的静力问题[J]. 计算结构力学及其应用,1993,(4):424-432. [8] 杨 敏, 艾智勇. 多层地基内部作用竖向集中力时的广义Mindlin课题解[C]//中国土木工程学会第八届土力学及岩土工程学术会议论文集. 1999. [9] 魏 纲,王 霄,张鑫海. 多因素下双线盾构隧道施工引起的土体变形研究[J]. 现代隧道技术,2018,55(3):130-139. doi: 10.13807/j.cnki.mtt.2018.03.018 [10] 邱明兵,高文生. Mindlin解积分的方形荷载竖向应力系数初等解[J]. 应用力学学报,2021,38(2):655-662. doi: 10.11776/cjam.38.02.D113 [11] 唐晓武,朱 季,刘 维,等. 盾构施工过程中的土体变形研究[J]. 岩石力学与工程学报,2010,29(2):417-422. [12] 梁荣柱,夏唐代,林存刚,等. 盾构推进引起地表变形及深层土体水平位移分析[J]. 岩石力学与工程学报,2015,34(3):583-593. doi: 10.13722/j.cnki.jrme.2015.03.016 [13] 王智德,江俐敏,饶 宇. 基于时空关系的盾构开挖地表沉降规律[J]. 土木与环境工程学报(中英文),2019,41(1):62-69. [14] 邓皇适,傅鹤林,史 越. 小转弯半径曲线盾构隧道开挖引发地表沉降计算[J]. 岩土工程学报,2021,43(1):165-173. [15] 魏 纲,庞思远. 双线平行盾构隧道施工引起的三维土体变形研究[J]. 岩土力学,2014,35(9):2562-2568. doi: 10.16285/j.rsm.2014.09.024 [16] 艾智勇,杨 敏. 多层地基内部作用一水平力时的扩展Mindlin解[J]. 同济大学学报(自然科学版),2000,(3):272-276. doi: 10.3321/j.issn:0253-374X.2000.03.005 [17] 余 力,黄美纯,陈文忠,等. 离散Hankel变换(英文)[J]. 计算物理,1998,(1):90-95. doi: 10.19596/j.cnki.1001-246x.1998.01.015 -




 下载:
下载: