Flow State of Single Rough Fracture Based on Lattice Boltzmann Method
-
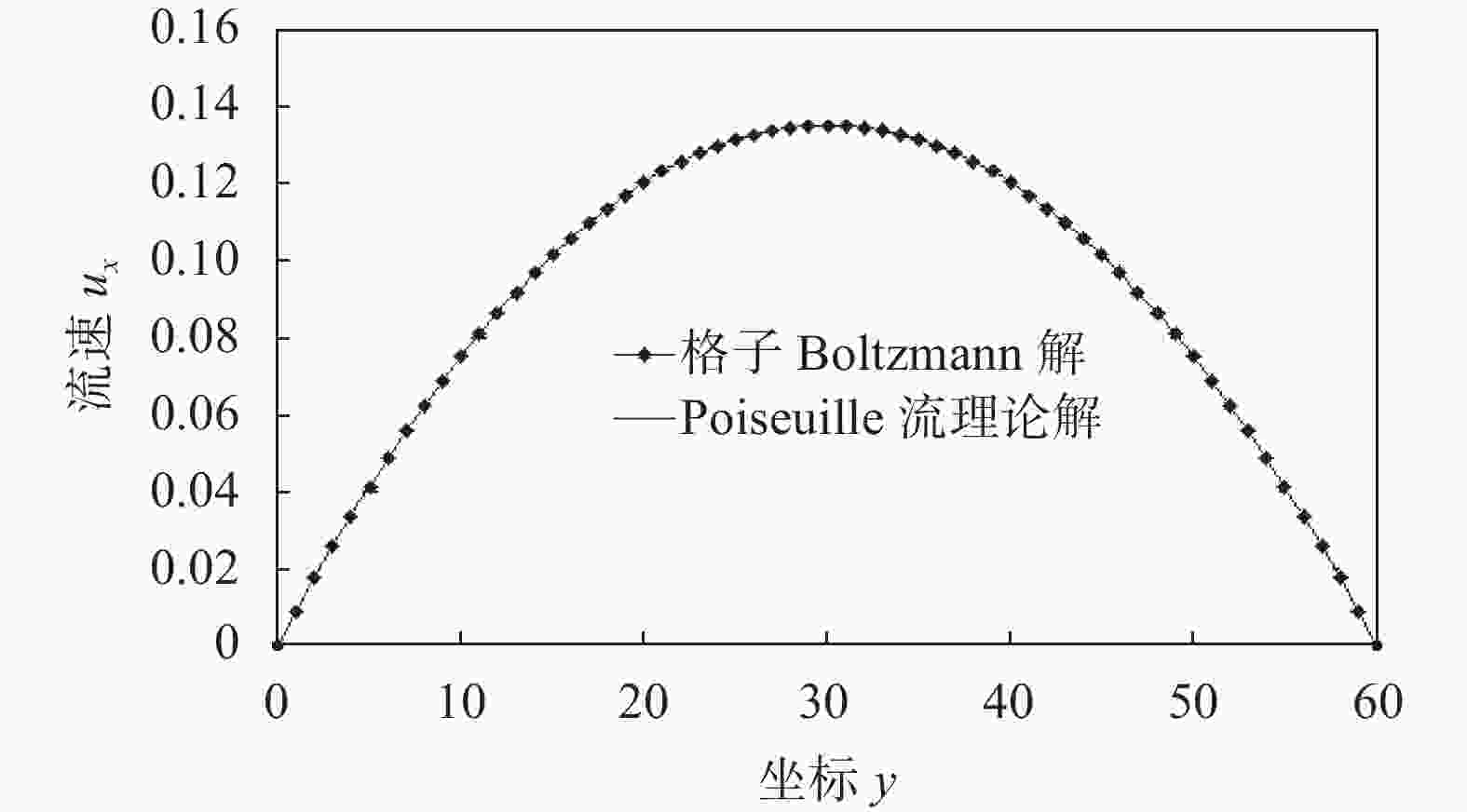
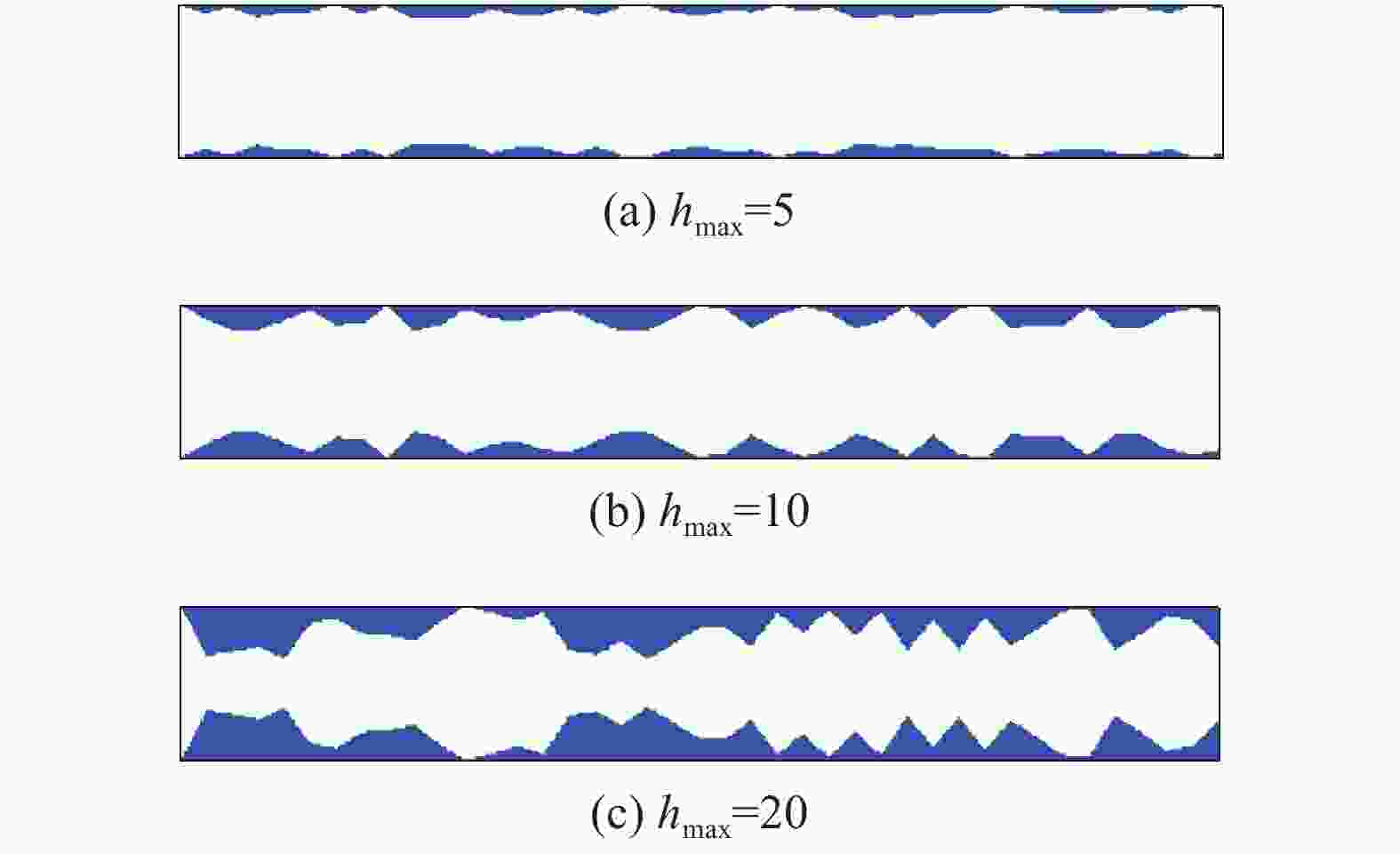
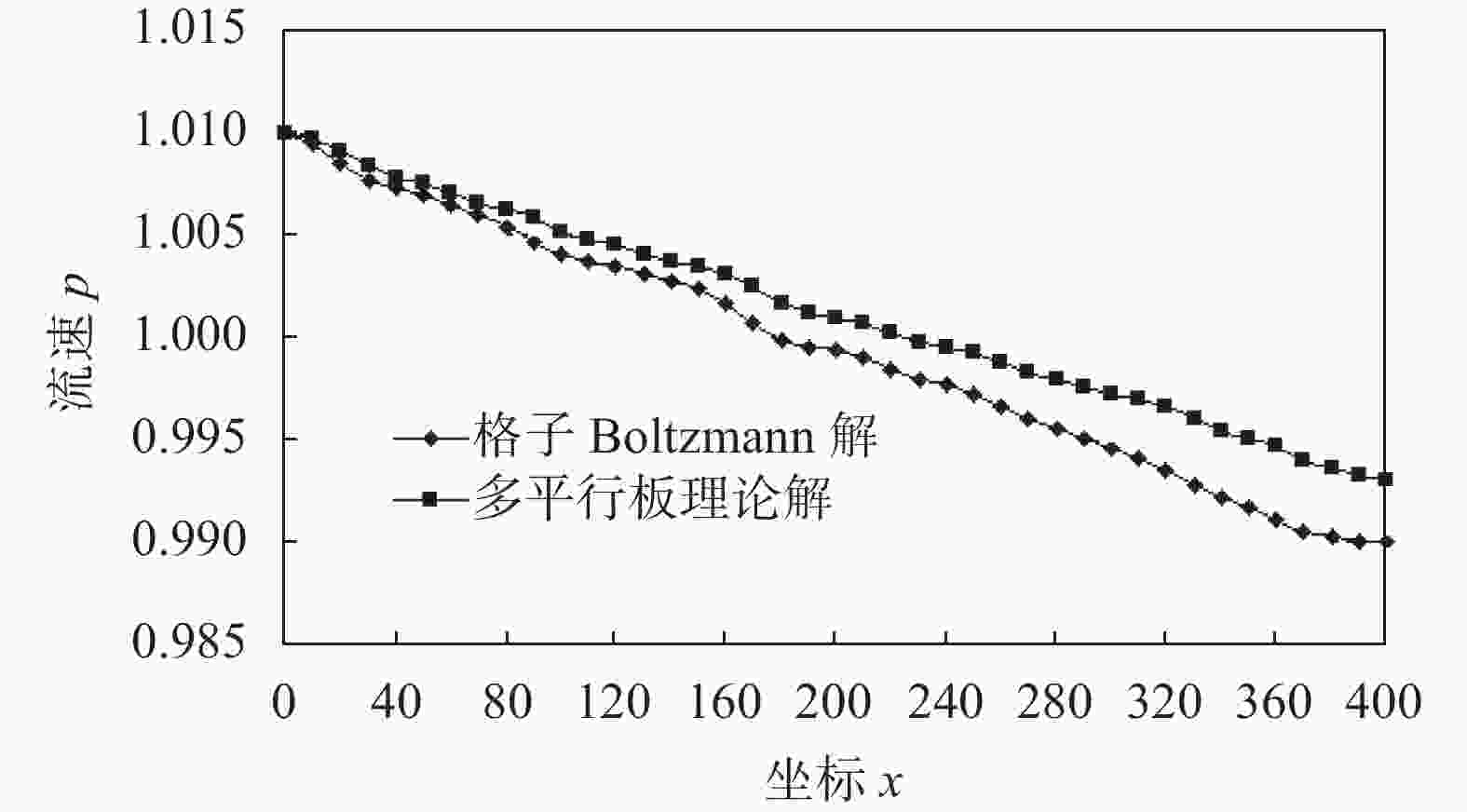
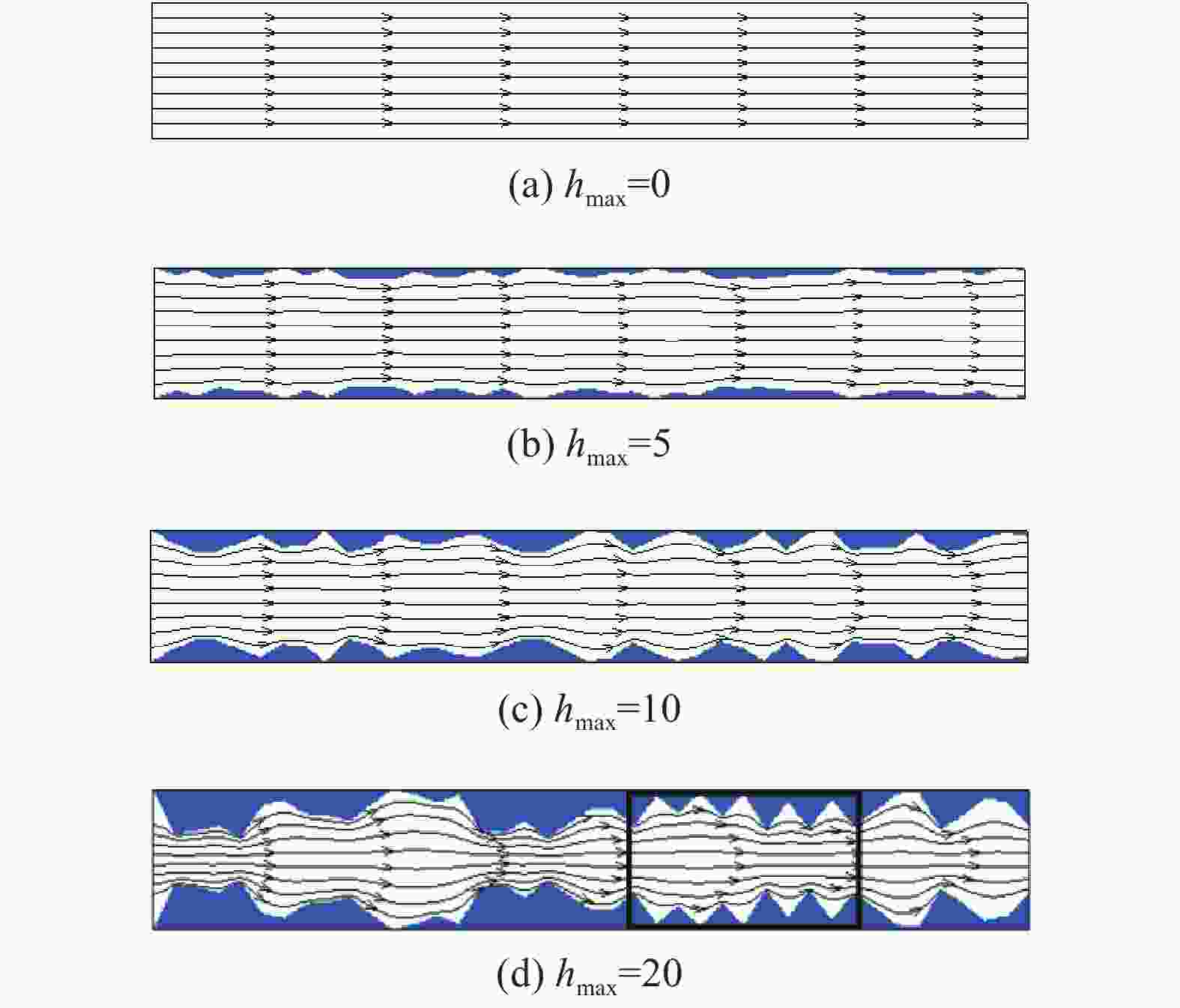
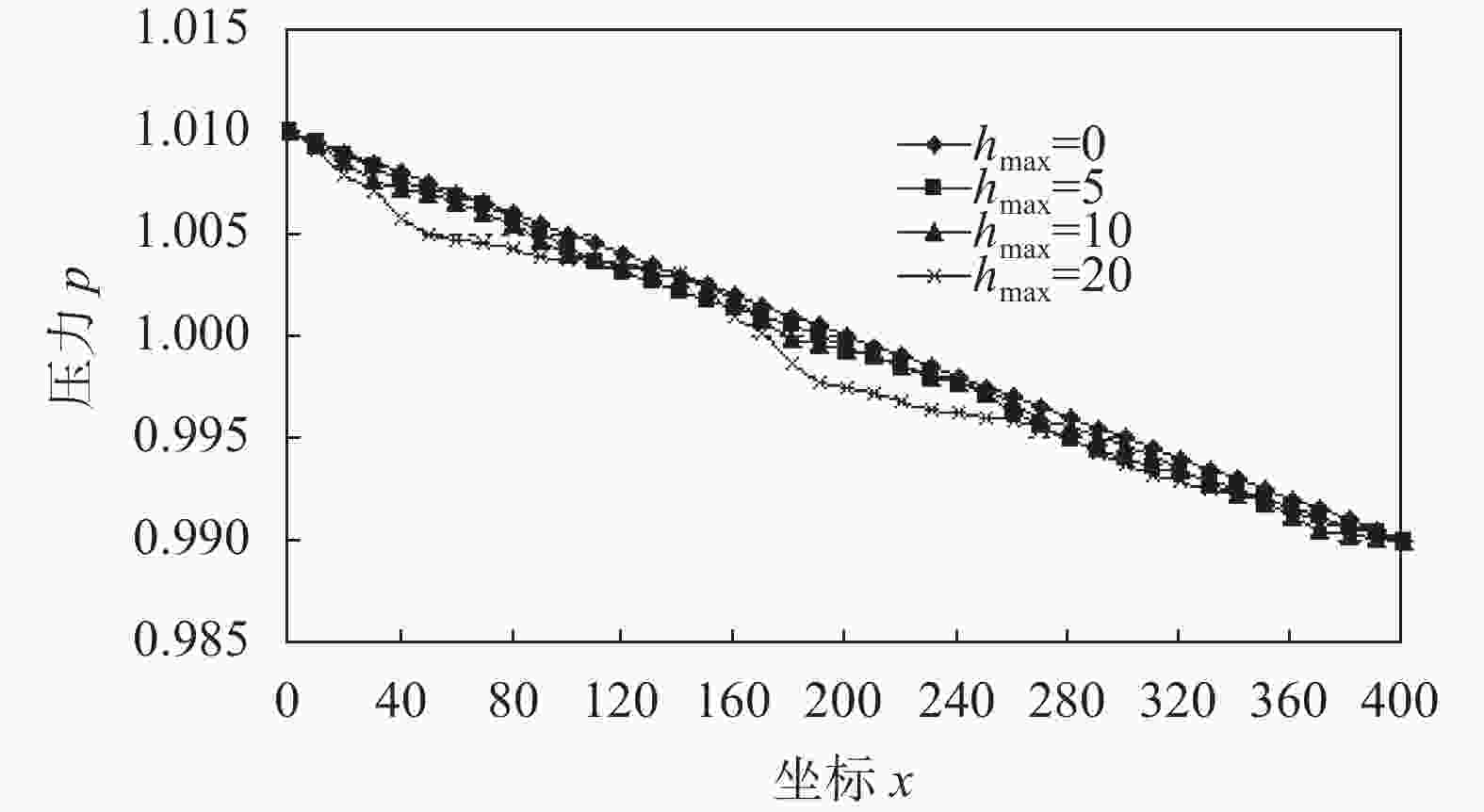
摘要: 岩体中普遍存在裂隙,基于格子Boltzmann方法以及D2G9离散模型在计算流体的渗流状态下具有边界条件易于设置、计算效率较高、计算结果可视化等优点,建立考虑不同粗糙度的单一裂隙渗流模型,模型的上下边界设置为无滑移的全反弹边界,左右边界则采用非平衡外推格式的分布函数边界,同时结合经典流体力学的Poiseuille流问题,对计算模型进行验证。最后,分析岩体裂隙表面粗糙程度对渗流状态的影响,计算结果表明:随壁面粗糙程度的增加,流体的流速、大小、方向均会发生不同程度的改变,并且在由粗糙度的改变而引起隙宽急剧变化的部位,局部伴随着流体旋涡的形成,导致流体内部摩擦阻力的增大,从而产生较大的局部能量损耗。
-
关键词:
- 岩体渗流 /
- 格子Boltzmann方法 /
- 单一粗糙裂隙渗流
Abstract: Based on the lattice Boltzmann method and D2G9 discrete model, a single fracture seepage model was established considering different roughness, with the advantages of the easy setting of boundary conditions, high computational efficiency, and visualization of calculation results. The upper and lower boundaries of the model were set as full rebound boundaries without slip. The distribution function boundary of the left and right edges was used in the non-equilibrium extrapolation format, and the model is verified with the Poiseuille flow problem of classical fluid mechanics. Finally, the influence of the surface roughness of rock fracture on the seepage state was analyzed. The calculation results showed that with the increase of the roughness of the wall surface, the flow velocity, size, and direction of the fluid will change to different degrees. In the parts where the gap width changes sharply due to the change of roughness, the formation of local fluid vortices will lead to the increase of internal friction resistance of the fluid, resulting in greater local energy loss.-
Key words:
- rock mass seepage /
- Lattice Boltzmann method /
- single rough fracture flow
-
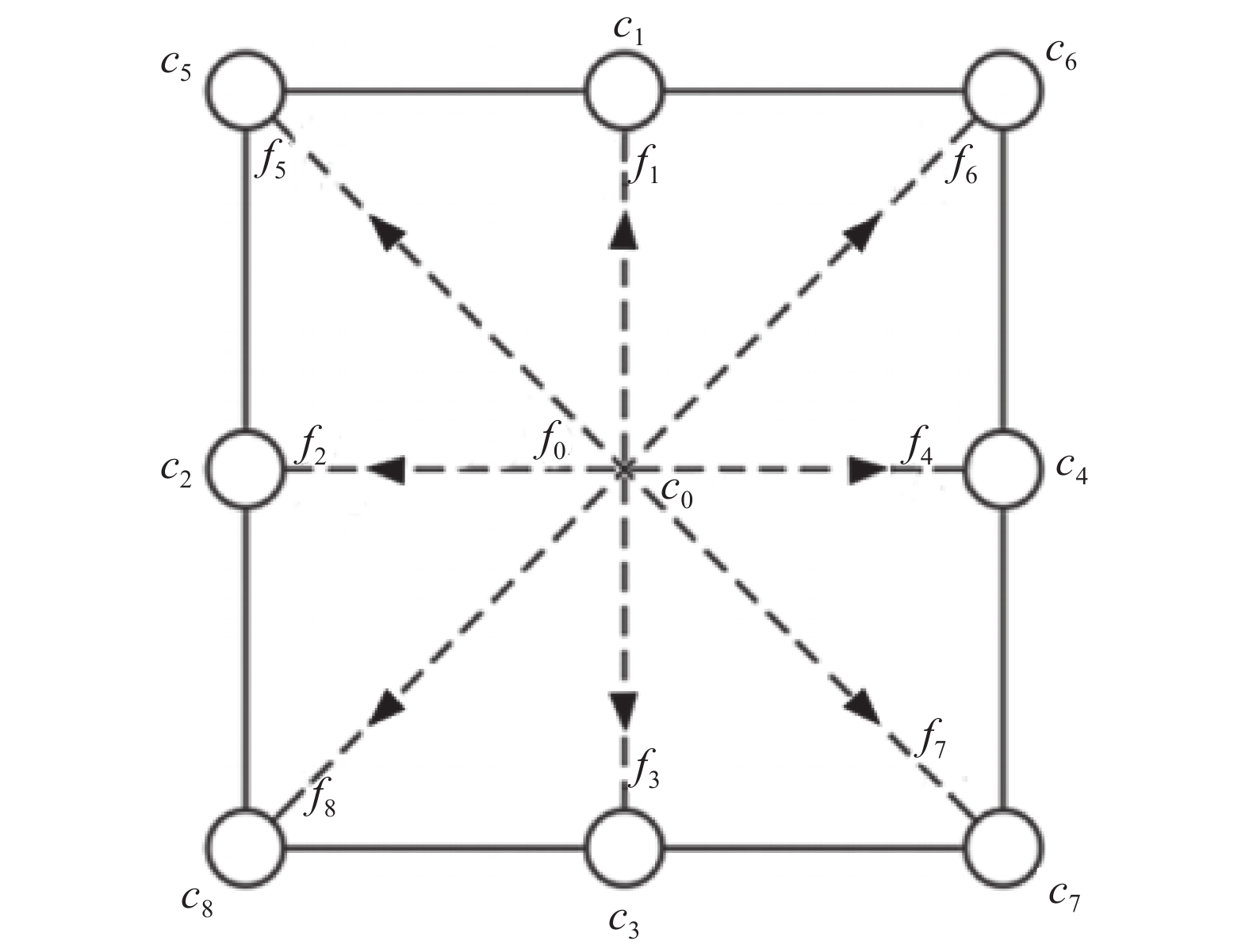
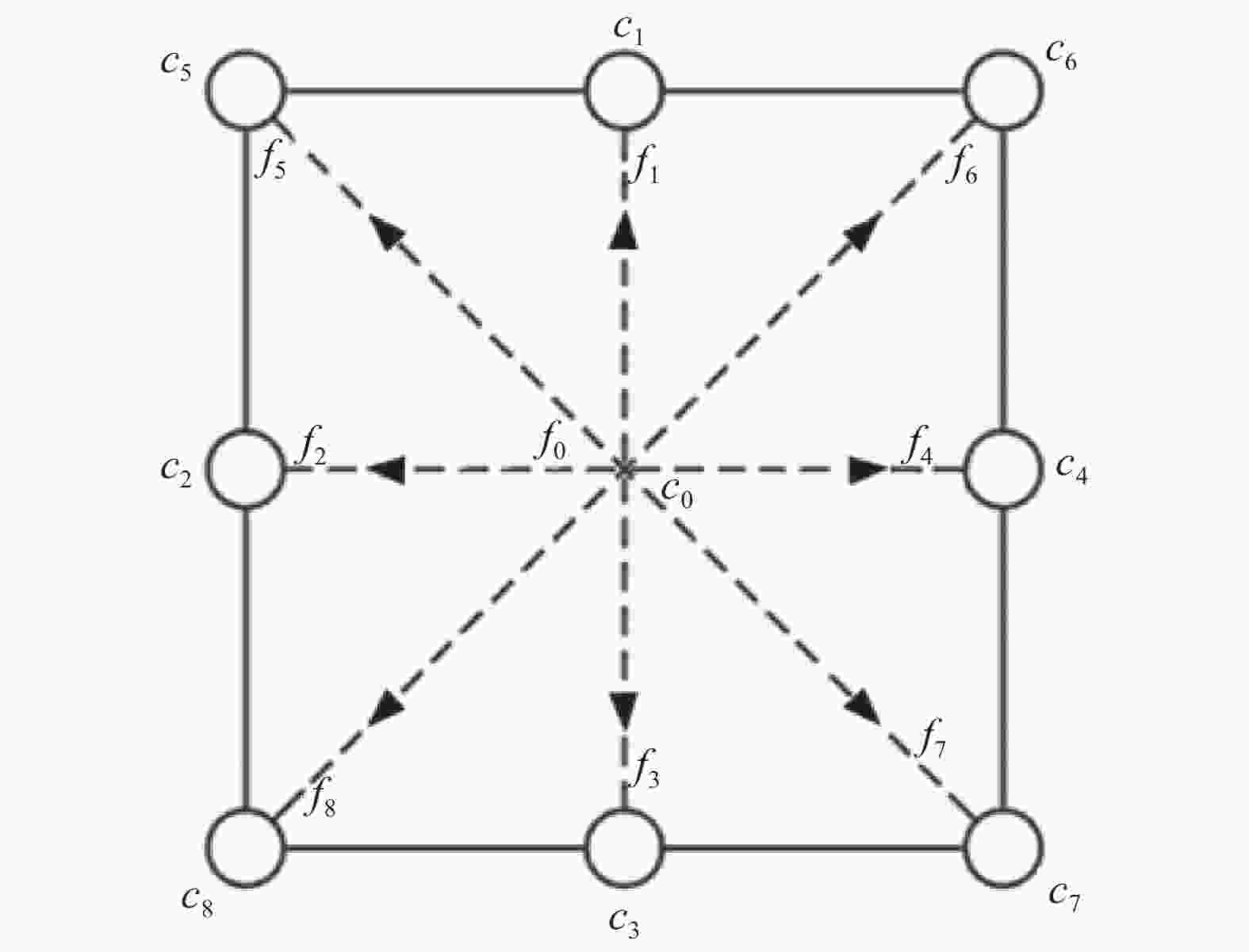
图 1 D2G9模型示意图[9]
-
[1] 刘日成, 蒋宇静, 李 博, 等. 基于逆Broyden秩1拟牛顿迭代法的岩体裂隙网络渗流特性研究[J]. 岩土力学,2016,37(1):219-228. [2] 陈益峰, 周创兵, 盛永清. 考虑峰后力学特性的岩石节理渗流广义立方定律[J]. 岩土力学,2008,29(7):1825-1831. [3] 张 霞, 李凤滨, 盛金昌, 等. 格子Boltzmann方法模拟土体渗流场研究[J]. 水电能源科学,2012,30(10):61-64. [4] 盛金昌, 王 璠, 张 霞, 等. 格子Boltzmann方法研究岩石粗糙裂隙渗流特性[J]. 岩土工程学报,2014,36(7):1213-1217. [5] 朱益腾. 基于LB方法平板流立方定律的数值模拟研究[J]. 价值工程,2017,36(10):94-97. [6] 田忠伟, 赵志刚, 周 亚, 等. 基于格子Boltzmann方法的裂隙介质渗流模拟研究[J]. 煤炭技术,2017,36(11):181-183. [7] 董武书, 张 跃. 单一裂隙渗流的格子Boltzmann数值模拟[J]. 煤炭技术,2021,40(1):82-85. [8] 鲁俊杰. 花岗岩裂隙等效水力隙宽表征及渗透特性研究[D]. 南京: 南京大学, 2019. [9] GUO Z L, SHI B C, WANG N C. Lattice BGK model for incompressible Navier-Stokes equation[J]. Journal of Computational Physics,2000,165:288-306. doi: 10.1006/jcph.2000.6616 [10] 郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2008. [11] 何雅玲, 王 勇, 李 庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2008. [12] SUKOP M C, THORNE D T. Lattice Boltzmann Modeling: An Introduction for Geoscientists and Engineers[M]. Berlin: Springer Verlag, 2006. [13] GUO Z L, ZHENG C G, SHI B C. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method[J]. Chinese Physics,2002,11(4):366-374. doi: 10.1088/1009-1963/11/4/310 -




 下载:
下载: