A New Model for Estimating VS30 Based on Engineering Boreholes Data
-
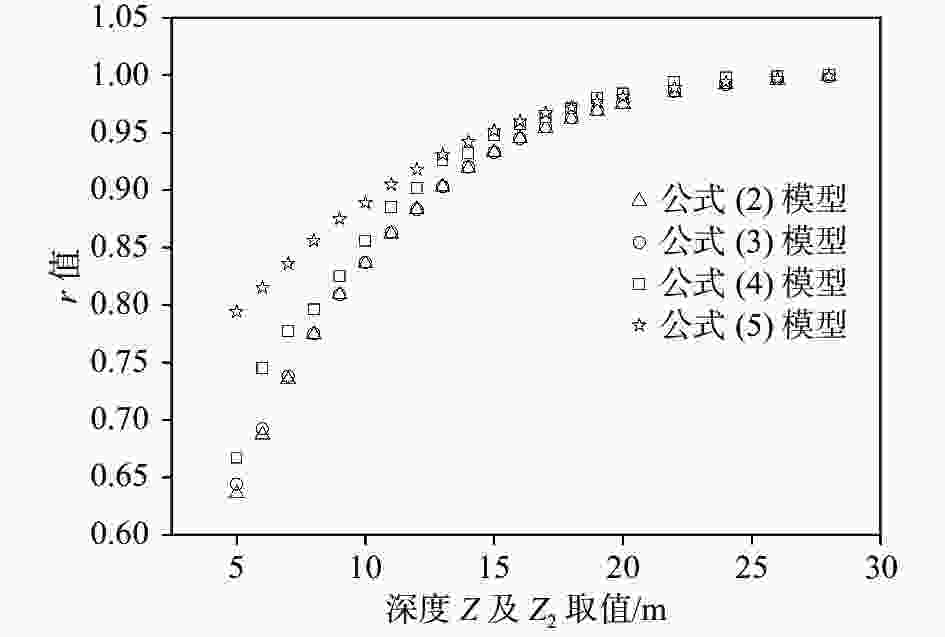
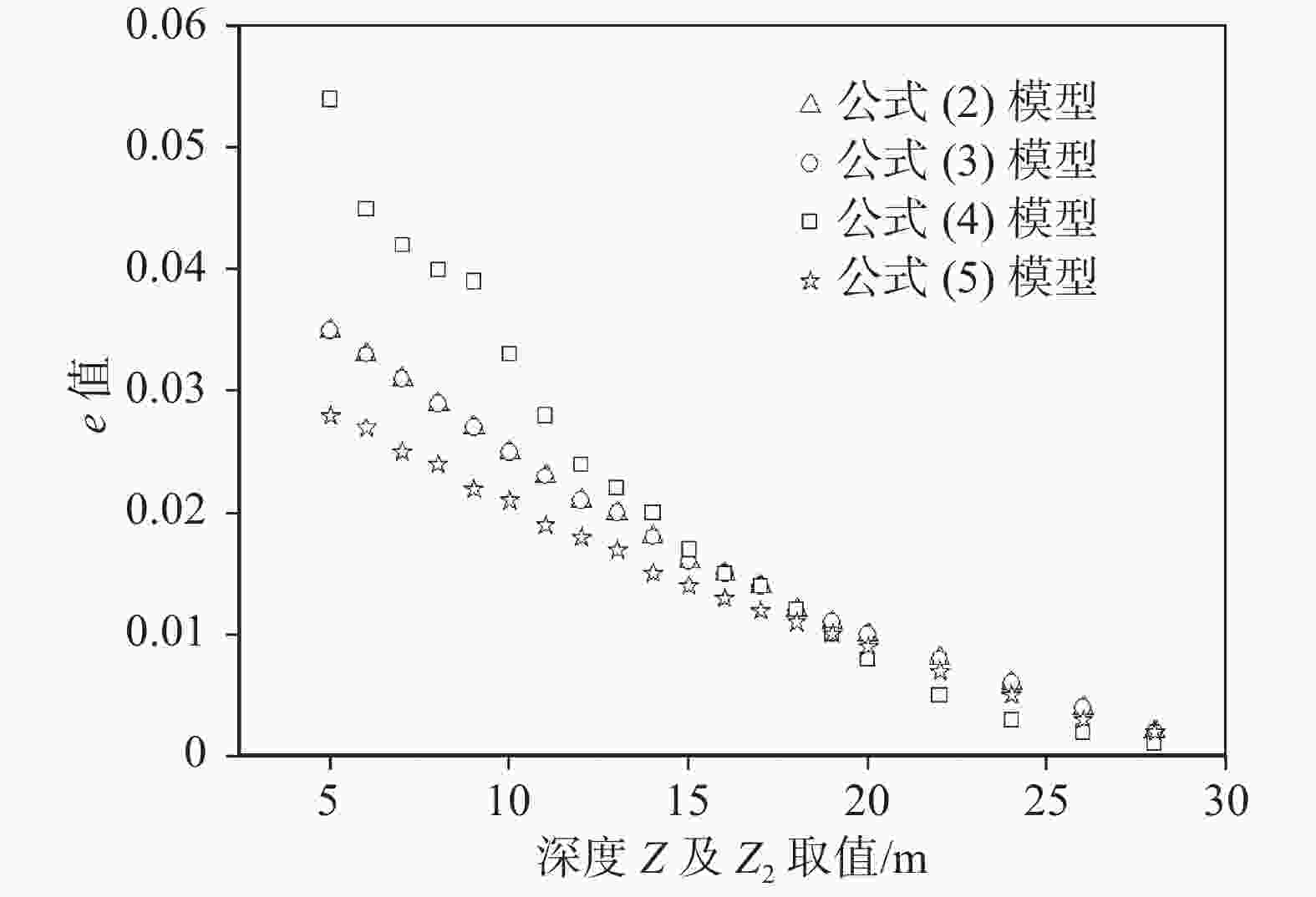
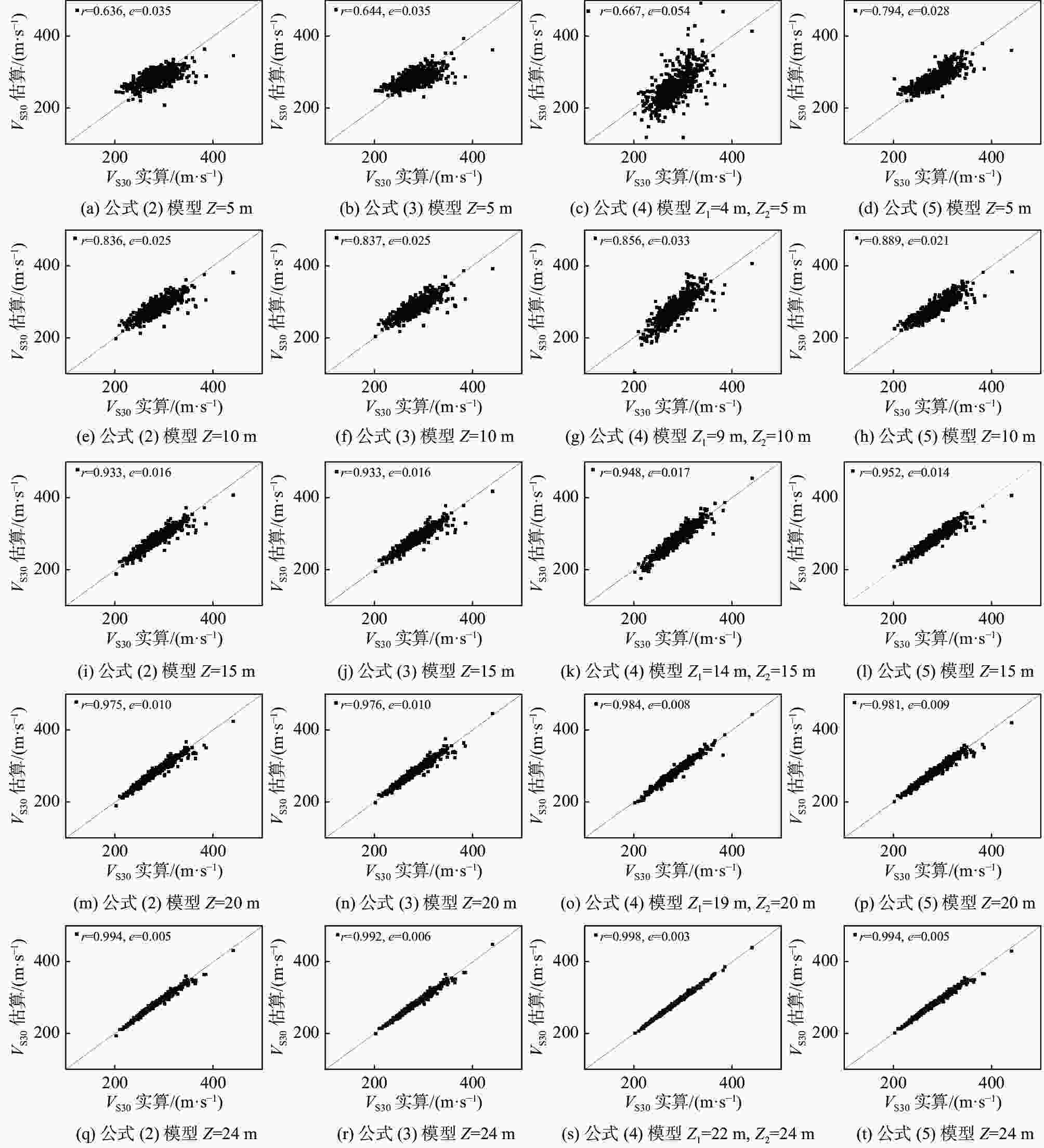
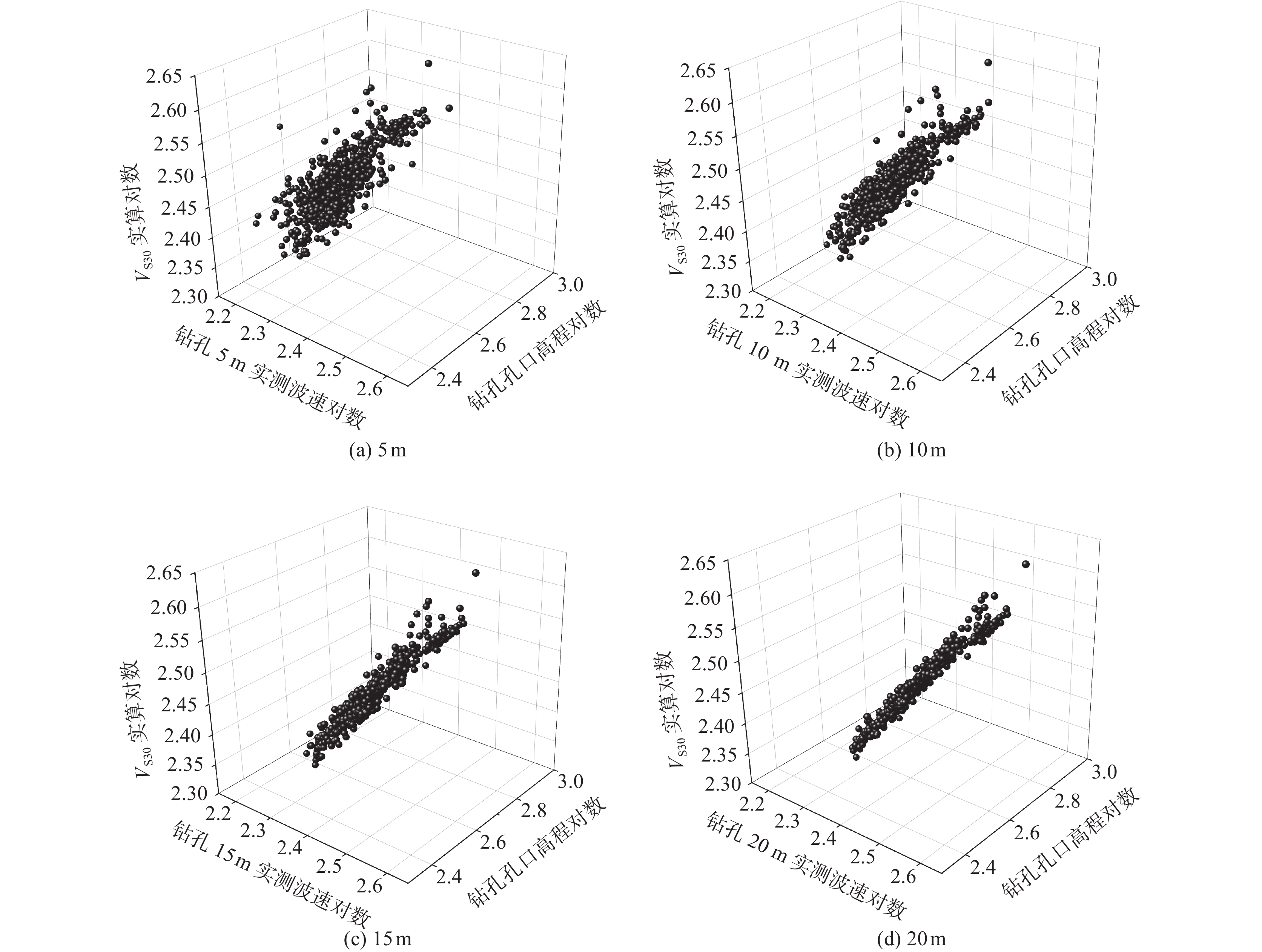
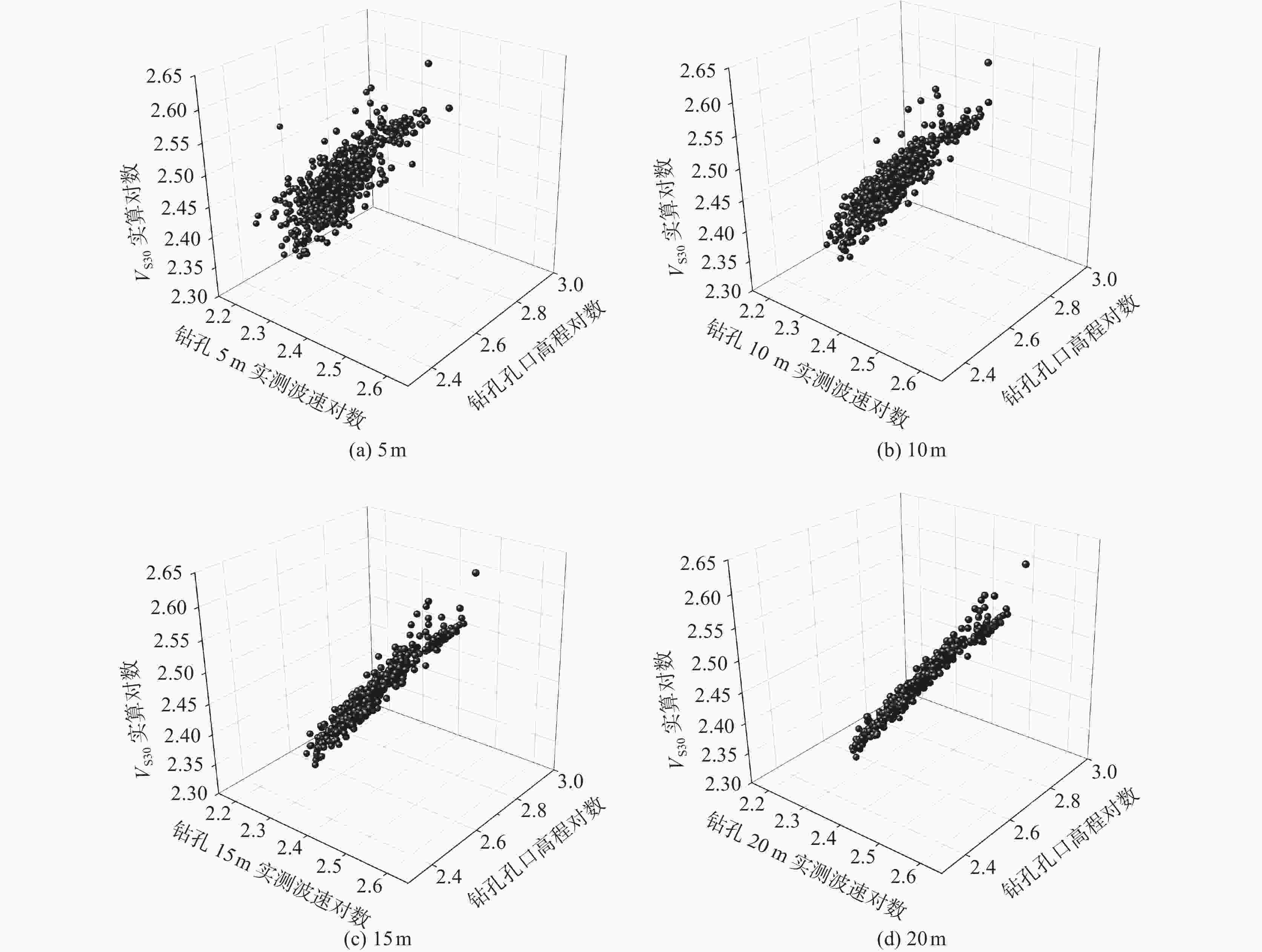
摘要: 地表以下30 m深度的平均剪切波速(VS30)是评价场地条件及场地地震影响的重要参数。我国存在大量深度小于30 m的钻孔数据,此类钻孔无法直接计算得到VS30,阻碍了VS30相关研究成果的推广应用,因此准确估算VS30尤为重要。基于陕西关中平原4个城市590个孔深大于30 m的钻孔测井数据,采用拟合、对比方法开展VS30估算模型研究。研究发现:钻孔不同深度的平均剪切波速(深度Z<30 m)及孔口高程与实算VS30沿深度呈现较强的对数线性相关性,并由此提出了基于钻孔不同深度平均剪切波速及孔口高程的VS30估算对数线性外推新型模型,简称双因素影响外推估算模型。相比速度梯度、双深度参数模型,在计算深度取值越小时,新型模型估算精度越高,稳定性越好,优势越突出。Abstract: The average shear wave velocity to a depth of 30 m below the ground surface (VS30) is an important parameter for evaluating the site condition and the site earthquake response. There are a large number of borehole data with depths of less than 30 m in China, and these borehole data cannot be directly used to calculate VS30 by definition equation code. Under this situation, referencing the correlated research results which include the parameter of VS30 were prevented. It is important to estimate VS30 accurately. Using the data of 590 boreholes with depths greater than 30 m in Guanzhong plain of Shaanxi Province to research the VS30 estimation model. The results show that the average shear wave velocity at different depths (Z<30 m) and the elevation of the borehole have a strong log-linear relationship with the measured value of VS30 along the depth, so a new model of log-linear extrapolation, which comprehensively considers the average shear wave velocity at different depths and the elevation of the borehole, was proposed. Compared with the velocity gradient extrapolation model and the double-depth parameter extrapolation model, when the calculation depth is smaller, the new model has higher estimation accuracy and better stability, and this advantage is more prominent.
-
表 1 各模型计算的相关系数及总误差
深度Z或者Z2取值/m 公式(2)模型 公式(3)模型 公式(4)模型 公式(5)模型 r e r e r e r e 5 0.636 0.035 0.644 0.035 0.667 0.054 0.794 0.028 6 0.687 0.033 0.692 0.033 0.745 0.045 0.815 0.027 7 0.735 0.031 0.738 0.031 0.777 0.042 0.836 0.025 8 0.774 0.029 0.775 0.029 0.796 0.04 0.856 0.024 9 0.809 0.027 0.809 0.027 0.825 0.039 0.875 0.022 10 0.836 0.025 0.837 0.025 0.856 0.033 0.889 0.021 11 0.862 0.023 0.863 0.023 0.885 0.028 0.905 0.019 12 0.883 0.021 0.883 0.021 0.902 0.024 0.918 0.018 13 0.903 0.020 0.903 0.020 0.926 0.022 0.931 0.017 14 0.919 0.018 0.920 0.018 0.932 0.020 0.942 0.015 15 0.933 0.016 0.933 0.016 0.948 0.017 0.952 0.014 16 0.945 0.015 0.945 0.015 0.957 0.015 0.960 0.013 17 0.954 0.014 0.955 0.014 0.963 0.014 0.967 0.012 18 0.962 0.012 0.963 0.012 0.971 0.012 0.972 0.011 19 0.969 0.011 0.970 0.011 0.98 0.01 0.977 0.010 20 0.975 0.010 0.976 0.010 0.984 0.008 0.981 0.009 22 0.985 0.008 0.986 0.008 0.994 0.005 0.989 0.007 24 0.994 0.005 0.992 0.006 0.998 0.003 0.994 0.005 26 0.997 0.003 0.997 0.004 0.999 0.002 0.997 0.003 28 0.999 0.002 0.999 0.002 1.000 0.001 0.999 0.002 注:r为相关系数,e为总误差。 -
[1] GB 50011—2010 建筑抗震设计规范(2016年版)[S]. 北京: 建筑工业出版社, 2016. [2] European committee of standardization. EN 1998 Euro code 8: Design of structures for earthquake resistance -part 1: General Rules, Seismic Actions and Rules for Buildings[S]. Landon: Taylor and Francis, 1998. [3] Building seismic safety council (BSSC). Edition NEHRP recommended provision for seismic regulations for new buildings and other structures. FEMA 368/369[R]. Washington D C, 2001. [4] BOORE D M, STEWART J P M, EERI E S, et al. NGA-West2 equation for predicting PGA, PGV, and 5% damped PSA for shallow crustal earthquakes[J]. Earthquake Spectra,2014,30(3):1057-1085. doi: 10.1193/070113EQS184M [5] 李小军. 地震动参数区划图场地条件影响调整[J]. 岩土工程学报,2013,35(S2):21-29. [6] 江志杰, 彭艳菊, 吕悦军, 等. 工程地震中VS30估算模型及其应用研究进展[J]. 地震工程学报,2018,40(S1):76-82. [7] 江志杰, 彭艳菊, 方 怡, 等. 北京平原地区VS30估算模型适用性研究[J]. 震灾防御技术,2018,13(1):75-86. doi: 10.11899/zzfy20180107 [8] 丁莹莹, 邱德勋, 吴常雪, 等. 关中平原极端降水时空变化及其与大气环流的关系[J]. 干旱区研究,2022,39(1):104-112. [9] 黄丹青, 毛南赵. 关中盆地地貌类型及新构造运动分析[J]. 重庆科技学院学报(自然科学版),2018,20(1):1-5. [10] 宋友桂, 兰敏文, 刘慧芳, 等. 关中盆地新升界地层划分对比与第四纪下限[J]. 地质科技通报,2021,40(2):24-35. [11] KUO C H, WEN K L, HSIEH H H, et al. Evaluating empirical regression equations for VS and Estimating VS30 in northeastern Taiwan [J]. Soil Dynamics and Earthquake Engineering, 2011, 31(3): 431-439. [12] BOORE D M. Estimating VS30(or NEHRP Site Classes) from shallow velocity medels (depth<30 m)[J]. Bulletin of the Seismological Society of America,2004,94(2):591-597. doi: 10.1785/0120030105 [13] BOORE D M, THOMPSON E M, CADET H. Regional correlations of VS30 and velocities averaged over depths less than and greater than 30 m[J]. Bulletin of the Seismological Society of America,2011,101(6):3046-3059. doi: 10.1785/0120110071 [14] 亢川川, 俞言祥, 马 超, 等. 四川地区深度小于30 m钻孔的VS30估计方法[J]. 震灾防御技术,2015,10(2):316-323. doi: 10.11899/zzfy20150211 [15] 张炜超, 孙 昱, 田勤虎, 等. 陕西关中平原地区VS30估算模型研究[J]. 土工基础,2022,36(5):760-764. [16] WANG H Y, WANG S Y. A new method for estimating VS30 from a shallow-wave velocity profile (depth < 30 m)[J]. [J]. Bulletin of the Seismological Society of America,2015,105:1359-1370. doi: 10.1785/0120140103 [17] MATSUOKA M, WAKAMATSU K, FUJIMOTO F, et al. Average shear-wave velocity mapping using Japan engineering geomorphologic classification map[J]. Structural Engineering and Earthquake Engineering,2006,23(1):57-68 doi: 10.2208/jsceseee.23.57s -




 下载:
下载: