Softening characteristics of anchorage interface in the fully grouted anchorage system
-
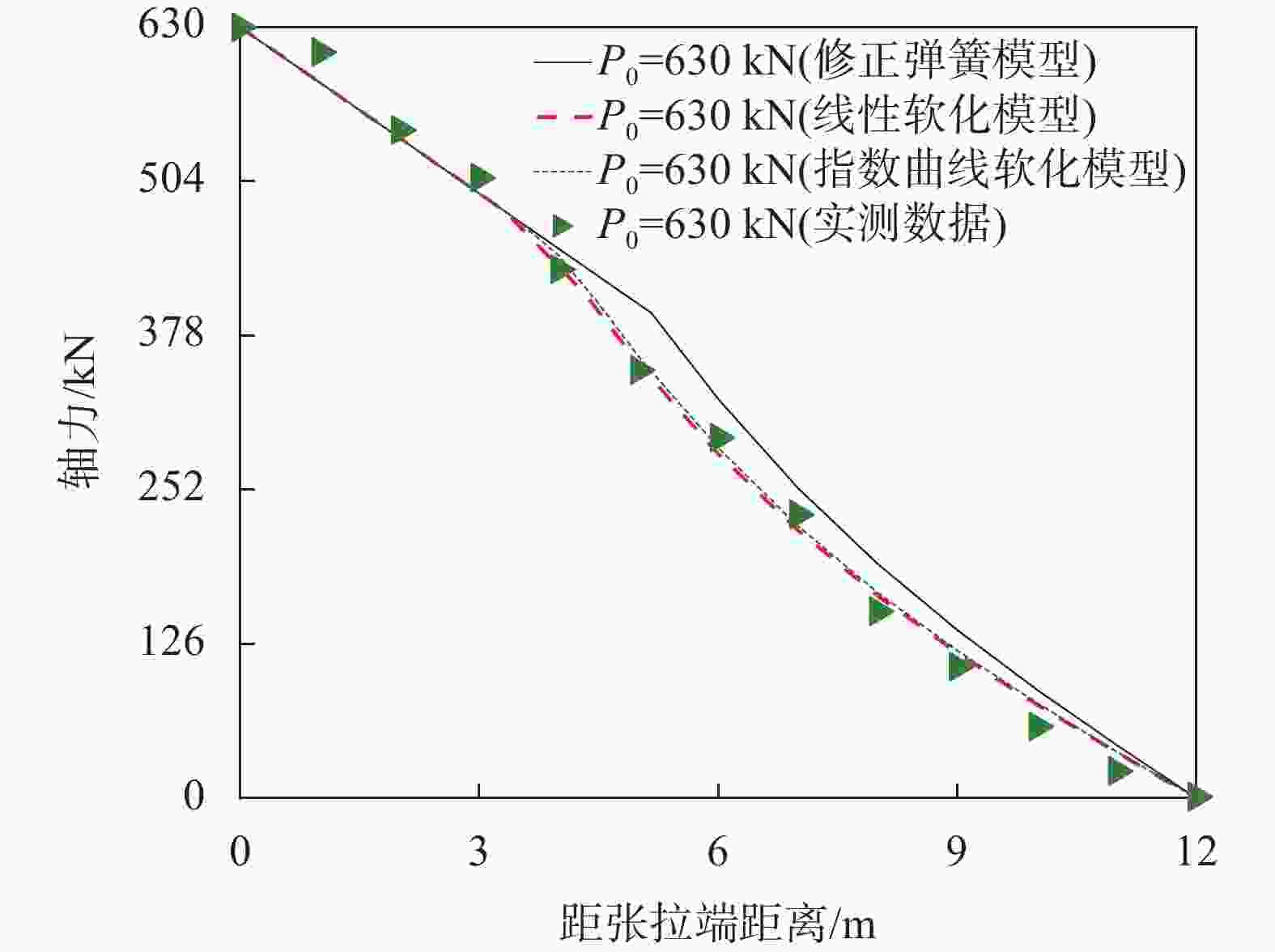
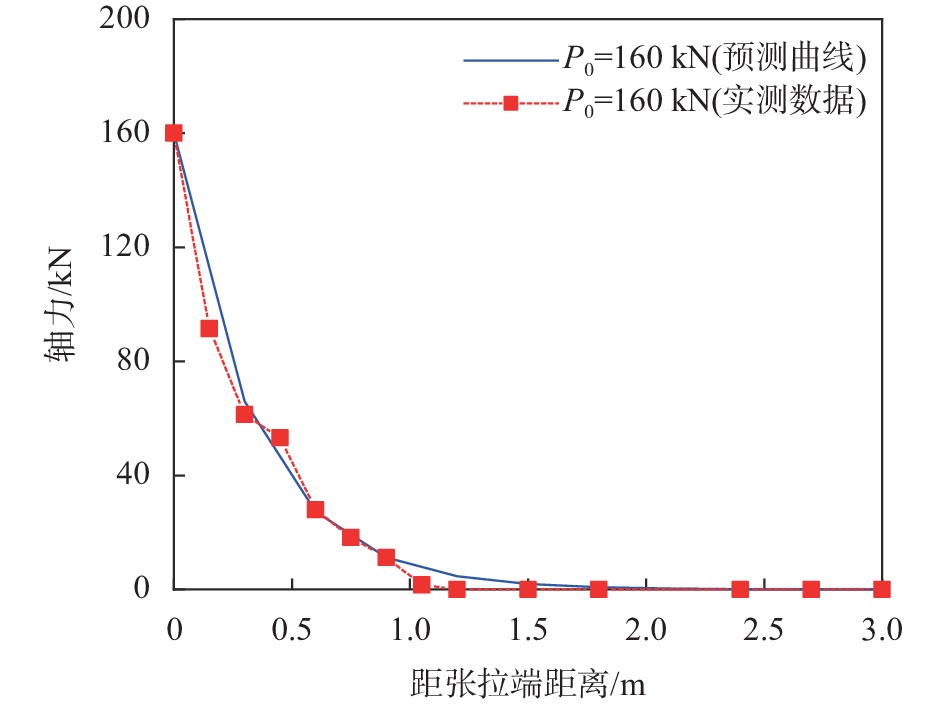
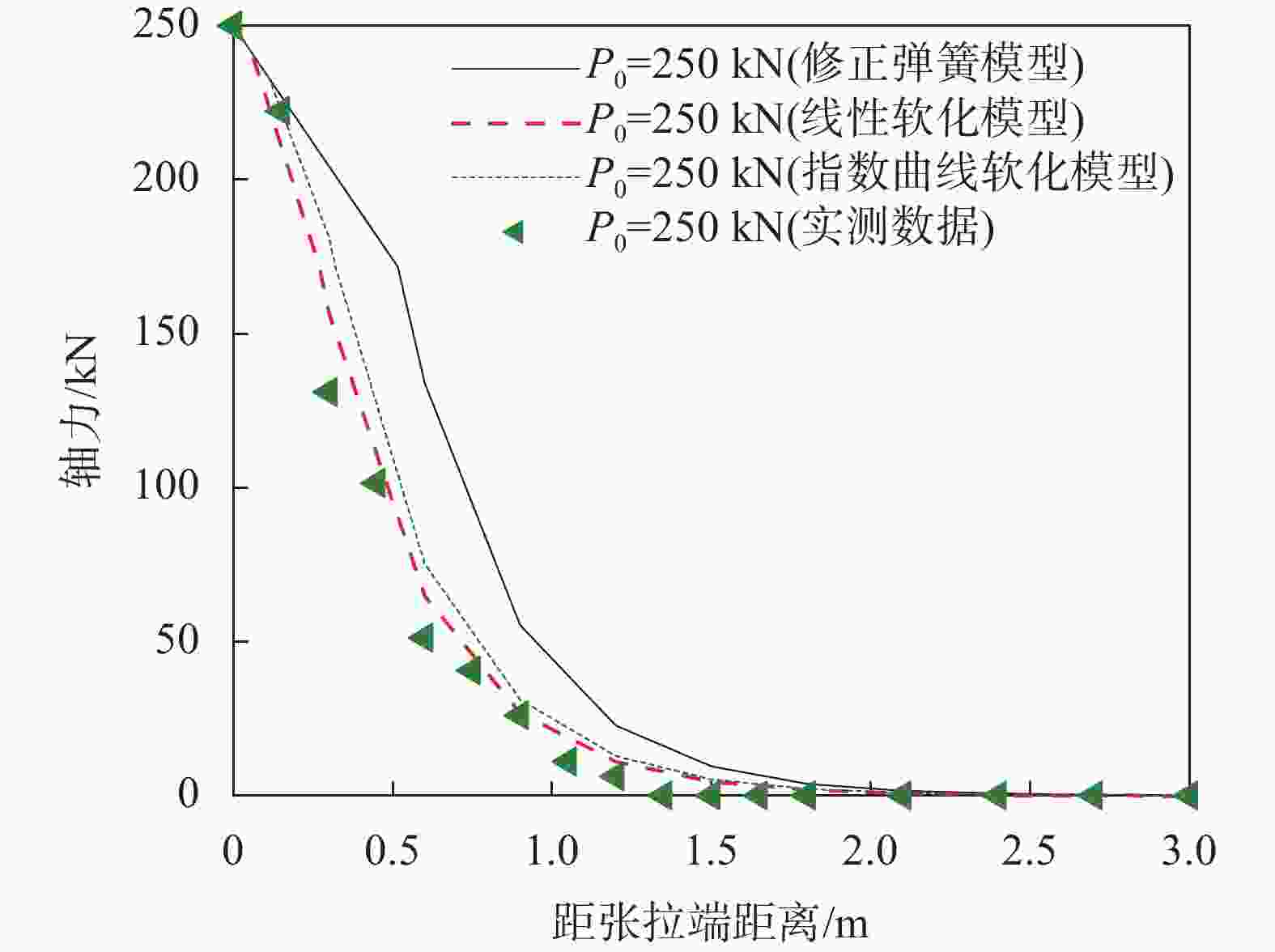
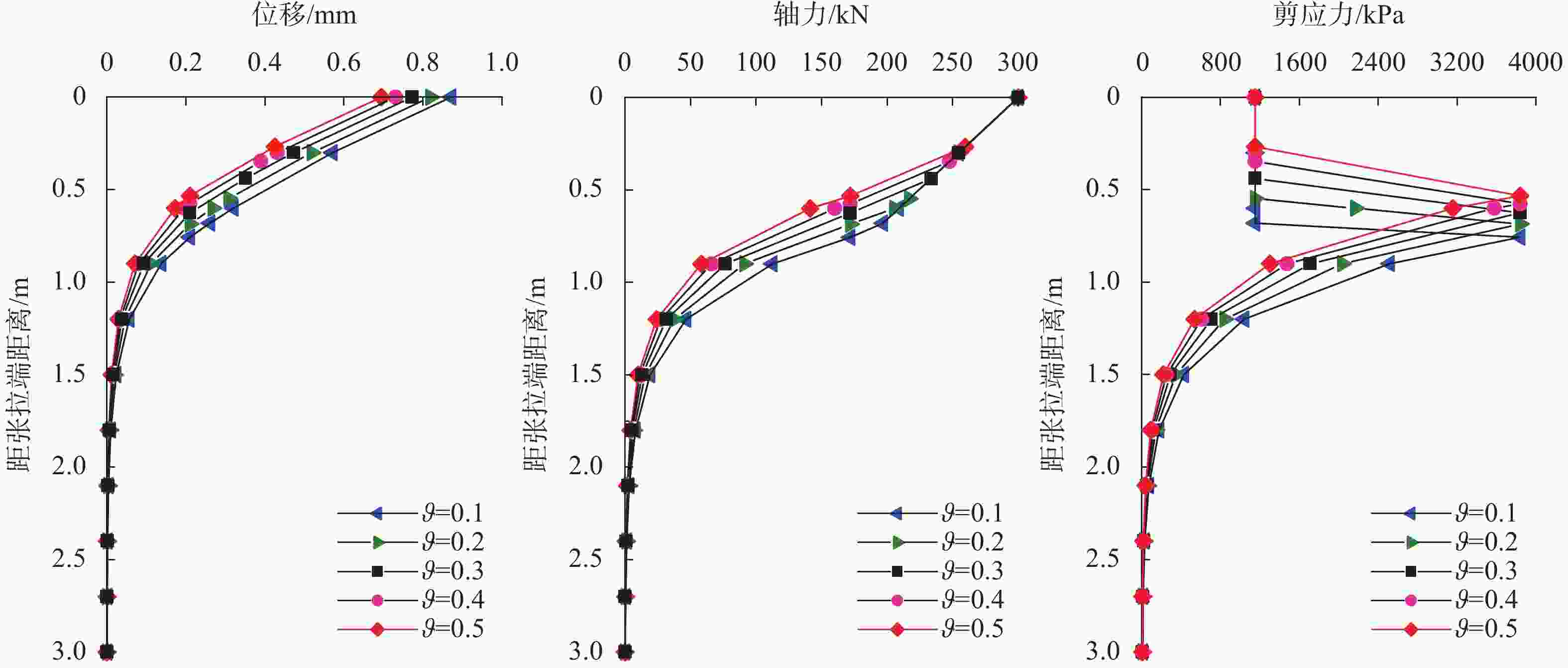
摘要: 基于离散化思想，将弹簧单元法引入锚固系统力学分析中，建立了位移分布函数、轴力分布函数以及侧阻力分布函数之间的联系。考虑锚固界面的软化特性，假设极限侧阻力分别以线性和指数曲线两种形式衰减至残余摩阻力，模拟了锚固界面的软化过程，分析了界面软化特性对锚固系统拉拔力学行为的影响，并采用现场拉拔试验进行了验证。研究表明：考虑锚固界面软化特性可更加真实地反映锚固系统的受力变形特性，无论是线性软化还是指数曲线软化，在选取合适软化系数的情况下，两者的分析结果差异很小。Abstract: Based on the idea of discretization, the spring element method was introduced into the mechanical analysis of the anchorage system, and the relationship between the displacement distribution function, the axial force distribution function and the lateral resistance distribution function was established. Considering the softening characteristics of the anchorage interface, the softening process of the anchorage interface was simulated by assuming that the ultimate lateral resistance decays to the residual frictional resistance in the form of linear and exponential curves, respectively. The influence of interface softening characteristics on the pull-out mechanical behavior of the anchorage system was analyzed, and finally verified through on-site pull-out tests. Research has shown that considering the softening characteristics of the anchorage interface can more accurately reflect the stress deformation characteristics of the anchorage system. Whether it is linear softening or exponential curve softening, the difference in analysis results between the two is very small when appropriate softening coefficients are selected.
-
0. 引言
全长灌浆锚固系统的承载性能主要取决于筋体类型、浆体材料以及地层岩性等。锚固界面是锚固系统荷载传递的基本载体，其剪切变形特性，尤其是剪切变形过程模拟，是锚固系统拉拔荷载传递分析的重要依据[1−2]。由于锚固材料及其粘结界面存在非线性、非均质性及非连续性等力学特性，锚固界面的作用机理实际上非常复杂，对于剪切界面模型的研究也一直是岩土锚固工程研究的重点和热点[3]。
Cai等[4]采用锚固体–岩体界面的双线性粘结滑移本构模型，基于剪滞理论建立了不同类型锚杆轴向应力和锚固体–岩体界面剪应力分布的解析式；尤春安等[5]对岩体中锚固体的拔出破坏过程进行了分析，建立了灌浆材料–岩体界面的剪滞–脱粘模型；Benmokrane等[6]以及Ren等[7]采用锚固界面的三线性剪切滑移建立了全弹性、弹塑性以及全塑性状态下锚固段轴力和剪应力分布的解析解；Liu等[8]基于锚固界面力学行为分析，提出了滑片模型、弹簧模型、修正弹簧模型、弹簧拉动滑片模型以及弹簧–滑片模型等5种锚固界面线性荷载传递模型（见图1），通过案例分析验证了各种模型的适用性。
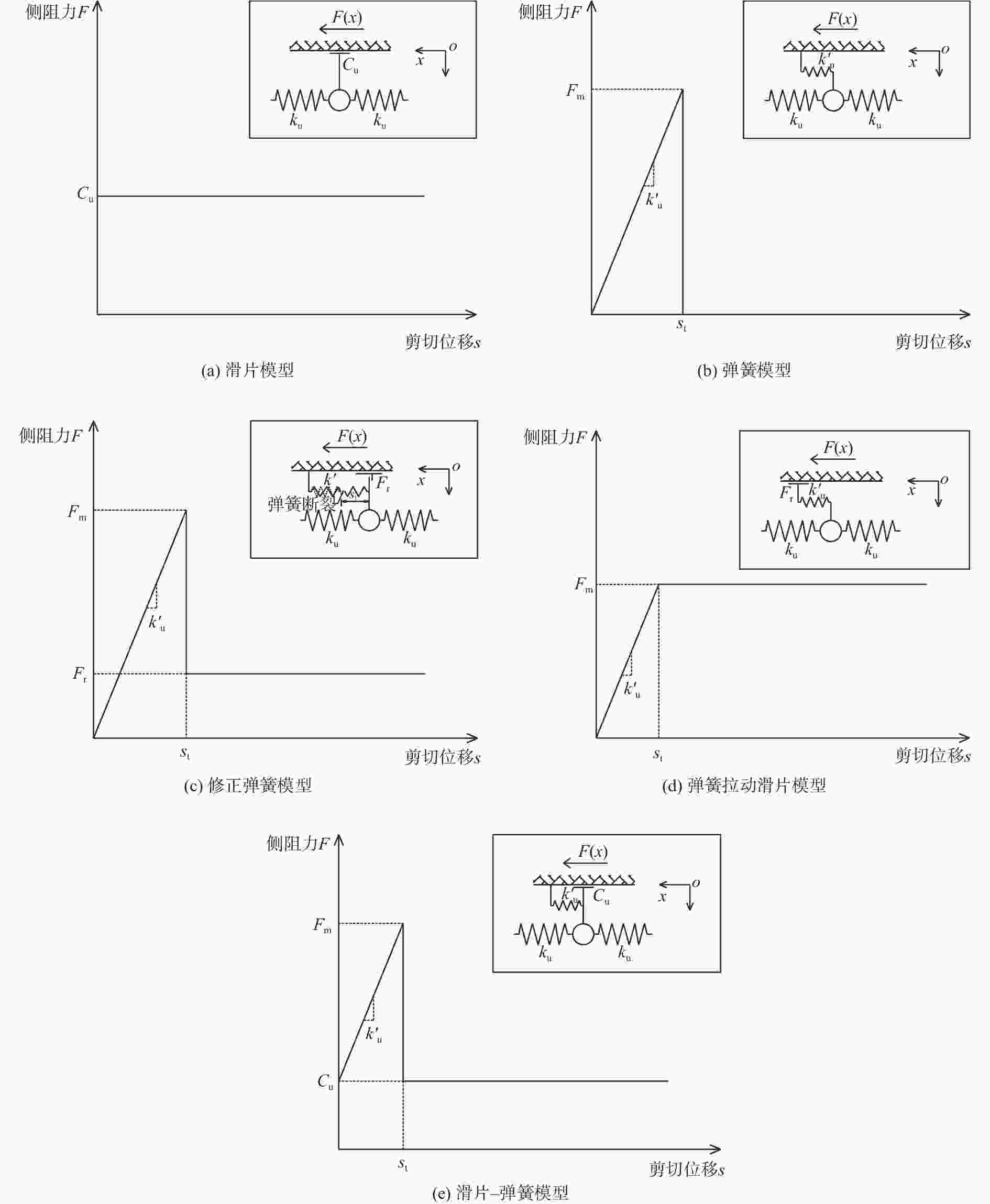
上述5种线性荷载传递模型假设当侧阻力达到极值后立即跌落至残余摩阻力，然而这只是理想的情况，实际工程中并非如此。由于灌浆锚固系统的锚固界面存在软化特性，锚固界面上的侧阻力由极值降至残余摩阻力，期间存在一个软化过程，以往研究[4,9−11]通过对锚固界面的剪切特性进行研究，也得出此结论。因此，在修正弹簧模型的基础上，假设极限侧阻力分别以线性和指数曲线两种形式衰减至残余摩阻力，来模拟锚固界面的软化过程，并分析界面软化特性对全长灌浆锚固系统拉拔力学行为的影响。
1. 锚固界面剪切滑移特性分析
《深圳市锚杆试验与检测技术标准》编制组在深圳市坪山新区海普瑞建设用地内主导了一场灌浆锚索的大型综合性试验（简称“深坪锚索综合试验项目”），试验现场见图2。该试验主要以采用多种方法测试岩土锚固系统的力学特性、长度及试验方法为主要目的。试验场地在锚索长度范围内地层单一，均为残积砂质黏性土。试验锚索有全长灌浆型、部分灌浆型、压力集中型、压力分散型、拉力扩孔型、压力扩孔型、二次注浆型、自测力型以及超长可回收型等共9种约180条，试验加卸载设备采用高精度自动控制系统以及实时无线数据传输技术，部分试验锚索采用分布式光纤测试灌浆体应变。本文选取其中埋设分布式光纤的5条全长灌浆锚索作为研究对象，分析其锚固界面的剪切滑移特性。
由分布式光纤监测到的灌浆体应变可整理出试验锚索各深度处的剪应力及对应剪切位移。由于灌浆体浅部变形较大，在较小的荷载下就已经发生了解耦，而灌浆体深部变形较小，在较大的荷载下仍处于弹性变形阶段，因此，结合现场试验情况，选取各试验锚索灌浆体–岩土体界面上1/3深度处的剪切滑移曲线作为分析对象，该深度处的灌浆体–岩土体界面上可反映出更为完整的剪切滑移过程，试验曲线如图3所示。由图3可以看出，各试验锚索灌浆体–岩土体界面上的剪切滑移曲线具有以下特征：当剪切位移较小时，剪应力随着剪切位移的增加而增长，两者有很明显的线性关系；当剪切位移超过某一定值后，随着剪切位移的增加，剪应力迅速减小；此后，随着剪切位移的进一步增加，剪应力呈缓慢减小趋势，几乎维持在一个较低的水平，即残余剪应力，这与以往研究[4,9−11]所得出的结论一致。由此可知，在锚固界面上至少经历了弹性变形、软化破坏以及滑移破坏三个阶段，大致反映了灌浆体–岩土体界面上的剪切变形过程。由图3还可以看出，试验锚索灌浆体–岩土体界面上的极限剪应力约为160 kPa，对应剪切位移约为3～8 mm，残余剪应力约为80 kPa。
2. 锚固系统受力分析
如图4所示，一根不计体力的均质等截面自由杆，在不受力的情况下可离散为n个相同的刚度均为k的质点弹簧单元。其作用是将每个杆微段等效为一根弹簧和一个质点的组合，在自由状态下其长度与自由杆微段长度相同，每个杆微段所受的外力均集中到对应弹簧元的质点上。在杆体两端施加相同的拉力P后，杆件伸长s，则每个弹簧元的伸长量Δsi均为s/n。由虎克定律可知：
$$ \mathrm{\Delta }{s}_{i}=\frac{Pl}{nEA} $$ (1) 式中：E，A，l分别为杆件弹性模量、截面积及长度。
则每个弹簧元的弹簧刚度系数为：
$$ k=\frac{nEA}{l} $$ (2) 同理，如图5所示，当杆件全长范围埋置于灌浆体或岩土体内时，在不受力的情况下杆件也可离散为n个刚度均为k的质点弹簧元。在杆顶施加拉力P后，张拉端产生位移s，由于杆体侧壁受到约束作用，此时每个弹簧元的伸长量Δsi均不相等，且符合下式：
$$ \mathrm{\Delta }{s}_{i}=\frac{{P}_{i}}{k} $$ (3) 式中：Pi为第i个弹簧元的弹簧拉力。
自张拉端开始，将弹簧元从1到n顺序编号，则第i个弹簧元和第i+1个弹簧元的位移有如下关系：
$$ {s}_{i}-{s}_{i+1}=\mathrm{\Delta }{s}_{i} $$ (4) 图6为第i个弹簧元的受力示意，弹簧元i不仅受到相邻弹簧元施加的拉力Pi和Pi-1，还受到杆体侧壁提供的侧阻力Fi，由此可知：
$$ {F}_{i}={P}_{i-1}-{P}_{i} $$ (5) 联立式（3）和式（5），可得：
$$ \mathrm{\Delta }{s}_{i-1}-\mathrm{\Delta }{s}_{i}=\frac{{F}_{i}}{k} $$ (6) 假使n→∞，当i从1到n变化时，则第i个弹簧元的位移si、弹簧拉力Pi以及受到的侧壁阻力Fi的分布形态，都可以分别近似为沿杆长的连续分布函数s(x)、P(x)以及F(x)，x为杆件埋深。结合式（4）可得位移分布函数s(x)的一阶导数：
$$ {s}'\left(x\right)=\underset{n\to \infty }{lim}\frac{-\mathrm{\Delta }{s}_{i}}{\left(\dfrac{l}{n}\right)} $$ (7) 二阶导数为：
$$ {s}''\left(x\right)=\underset{n\to \infty }{lim}\frac{\mathrm{\Delta }{s}_{i-1}-\mathrm{\Delta }{s}_{i}}{{\left(\dfrac{l}{n}\right)}^{2}} $$ (8) 则式（3）和（6）可分别转化为：
$$ s'\left(x\right)=-\frac{P\left(x\right)}{k\mathrm{_u}} $$ (9) $$ s''\left(x\right)=\frac{F\left(x\right)}{k\mathrm{_u}} $$ (10) 式中：ku为杆件单位长刚度，即：ku=kl/n=EA。对于其中弹性模量E的取值，当研究对象为杆体（或筋体）–灌浆体界面时可取筋体弹性模量Eb，当研究对象为灌浆体–岩土体界面时，可通过下面的公式计算：
$$ E\mathrm{_c}=\frac{E\mathrm{_b}A_{\mathrm{b}}+E\mathrm{_g}A_{\mathrm{g}}}{A_{\mathrm{b}}+A_{\mathrm{g}}} $$ (11) 式中：Ec为筋体和灌浆体的综合弹性模量；Eb为筋体弹性模量；Eg为灌浆体弹性模量；Ab为筋体截面积；Ag为灌浆体截面积。
式（9）建立了位移分布函数s(x)与轴力分布函数P(x)之间的联系，式（10）建立了位移分布函数s(x)与侧阻力分布函数F(x)之间的联系。
在应用弹簧单元法进行锚固系统受力分析时，可通过现场实测数据拟合或根据经验假定出侧阻力分布F(x)与位移分布函数s(x)之间的关系函数（也称荷载传递函数），代入式（10）进行微分方程的求解，从而得到具体的位移分布函数s(x)。将s(x)的一阶导数代入式（9）中可得到具体的轴力分布函数P(x)，将s(x)的二阶导数代入式（10）中可得到具体的侧阻力分布函数F(x)以及剪应力分布函数τ(x)。
事实上，弹簧单元法与荷载传递法在本质上是一致的，两者都需要先确定荷载传递函数，即τ(x)-s(x)曲线或F(x)-s(x)曲线。但是，弹簧单元法在推导过程中更为直观、明了、易于理解，且具有更为简洁的形式，方便求解。
3. 考虑界面软化特性的传力模型
3.1 线性软化模型
如图7所示，该模型假设当剪切位移大于侧壁弹簧的极限位移st时，其侧阻力开始由极限侧阻力Fm线性降低，在剪切位移达到s′t时降为残余侧阻力Fr。剪切位移s′t所对应的深度为x′t=(1−ϑ)xt，其中：ϑ为线性软化系数，且0≤ϑ≤1，可根据室内剪切试验或工程经验取值；xt为剪切破坏区深度处。由此可将侧阻力分布曲线划分为滑移区、软化区以及弹性变形区，各区内的侧阻力分布函数如下：
$$ F\left(x\right)=\left\{\begin{aligned} & k_{\mathrm{u}}'s\left(x\right) & & x\mathrm{_t}\le x\le l \\ & \frac{F_{\mathrm{m}}-F\mathrm{_r}}{\vartheta x\mathrm{_t}}\left(x-x_{\mathrm{t}}'\right)+F\mathrm{_r} & & x\mathrm{_t}'\le x\le x\mathrm{_t} \\ & F\mathrm{_r} & & 0\le x\le x\mathrm{_t}'\end{aligned}\right. $$ (12) 式中：k′u为锚固界面剪切刚度，其它参数见文献[8]。
$ k_{\mathrm{u}}'=F\mathrm{_m}/s\mathrm{_t} $ ，其值可通过如下计算获得。当灌浆体与岩土体特性相同时：
$$ k\mathrm{_u}'=\frac{2\text{π}G\mathrm{_g}}{\mathrm{ln}\left(\dfrac{R}{r_{\mathrm{b}}}\right)} $$ (13) 当灌浆体与岩土体特性不相同时：
$$ k\mathrm{_u}'=\frac{2\text{π}G_{\mathrm{g}}G\mathrm{_r}}{G\mathrm{_g}\mathrm{ln}\left(\dfrac{R}{r_{\mathrm{g}}}\right)+G\mathrm{_r}\mathrm{ln}\left(\dfrac{r_{\mathrm{g}}}{r_{\mathrm{b}}}\right)} $$ (14) 式中：Gg为灌浆体的剪切模量；Gr为岩土体的剪切模量；rb为杆体（或筋体）半径；rg为钻孔半径；R为锚固系统的影响半径，即变形区半径。
已知，边界条件：
$$ {\left.s\left(x\right)\right|}_{x=0}={s}_{0} $$ (15) $$ {\left.{s}'\left(x\right)\right|}_{x=0}=-\frac{{P}_{0}}{{k}_{{\mathrm{u}}}} $$ (16) $$ {\left.{s}'\left(x\right)\right|}_{x=l}=0 $$ (17) 式中：s0和P0分别为张拉端的位移和拉拔力。
将式（12）代入式（10）中，求解微分方程，结合边界条件式（15）—式（17），可求得锚固系统的位移分布函数为
$$ s\left(x\right)=\left\{\begin{aligned} & \frac{\mathrm{cosh}[\lambda(l-x)]}{\mathrm{cosh}[\lambda(l-x\mathrm{_t})]}s\mathrm{_t}\qquad\qquad\qquad x\mathrm{_t}\le x\le l \\ & \frac{D}{6k_{\mathrm{u}}}(x^3-x\mathrm{_t^3})+\frac{F_{\mathrm{r}}-Dx\mathrm{_t}'}{2k_{\mathrm{u}}}(x^2-x\mathrm{_t^2})+ \\ & \qquad\frac{Dx\mathrm{_t}'^2-2P_0}{2k_{\mathrm{u}}}\left(x-x\mathrm{_t}\right)+s\mathrm{_t}\quad\; \; \; x_{\mathrm{t}}'\le x\le x_{\mathrm{t}} \\ & \frac{F\mathrm{_r}}{2k_{\mathrm{u}}}x^2-\frac{P_0}{k_{\mathrm{u}}}x+s_0\qquad\qquad\qquad0\le x\le x\mathrm{_t}'\end{aligned}\right. $$ (18) 式（18）对x求导，并将s'(x)代入式（9）中，可得锚固系统轴力分布函数为
$$ P\left(x\right)=\left\{\begin{aligned} & \frac{\mathrm{sinh}[\lambda(l-x)]}{\mathrm{cosh}[\lambda(l-x_{\mathrm{t}})]}k_{\mathrm{u}}\lambda s_{\mathrm{t}}\qquad\qquad\; \; \; \; x\mathrm{_t}\le x\le l \\ & P_0 - \frac{\mathrm{\mathit{D}}}{2}x^2 - \left(F\mathrm{_r} - Dx_{\mathrm{t}}'\right)x-\frac{Dx\mathrm{_t}'^2}{2}\; \; x\mathrm{_t}'\le x\le x_{\mathrm{t}}'' \\ & P_0-F\mathrm{_r}x\qquad\qquad\qquad\qquad\quad\; \; 0\le x\le x_{\mathrm{t}}'\end{aligned}\right. $$ (19) 将式（18）代入式（12），可得锚固系统剪应力分布函数为
$$ \tau\left(x\right)=\left\{\begin{aligned} & \frac{\mathrm{cosh}[\mathit{\lambda}(l-x)]}{2\text{π}r\mathrm{cosh}[\mathit{\lambda}(l-x_{\mathrm{t}})]}k\mathrm{_u}'s\mathrm{_t} & & x_{\mathrm{t}}\le x\le l \\ & \frac{F_{\mathrm{m}}-F\mathrm{_r}}{2\text{π}r\vartheta x\mathrm{_t}}\left(x-x\mathrm{_t}'\right)+\frac{F_{\mathrm{r}}}{2\text{π}r} & & x\mathrm{_t}'\le x\le x\mathrm{_t} \\ & \frac{F\mathrm{_r}}{2\text{π}r} & & 0\le x\le x\mathrm{_t}'\end{aligned}\right. $$ (20) 式中：
$ \mathrm{\mathit{D}}=\left(F_{\mathrm{m}}-F_{\mathrm{r}}\right)/(\vartheta x\mathrm{_t}) $ ；r为筋体或锚固体半径。根据P(x)在x=xt处的连续性，可得张拉端拉拔力：
$$ P_0 = \frac{\mathrm{sinh}[\lambda(l - x\mathrm{_t})]}{\lambda\mathrm{cosh}[\lambda(l - x_{\mathrm{t}})]}F\mathrm{_m} + \frac{D}{2}(x\mathrm{_t^2} + x\mathrm{_t}'^2)+\left(F\mathrm{_r}-Dx_{\mathrm{t}}'\right)x\mathrm{_t} $$ (21) 对上式进行求解，即可求得xt。
式（21）两边对xt进行求导，并求解xt，即可求得在极限拉拔力P0max下的剪切面的临界破坏深度：
$$ {x}_{\mathrm{t}\mathrm{j}}=l-\frac{1}{2\lambda }\mathrm{ln}\frac{1+\sqrt{\dfrac{\left(1-\alpha \right)\left(2-\vartheta \right)}{2}}}{1-\sqrt{\dfrac{\left(1-\alpha \right)\left(2-\vartheta \right)}{2}}} $$ (22) 式中：
$ \alpha=F_{\mathrm{r}}/F_{\mathrm{m}} $ 。此时，锚固系统极限拉拔力为
$$ \begin{aligned}[b] & P_{0\mathrm{max}}=\frac{F_m}{\lambda}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left[\frac{1}{2}\mathrm{ln}\frac{1+\sqrt{\dfrac{\left(1-\alpha\right)\left(2-\vartheta\right)}{2}}}{1-\sqrt{\dfrac{\left(1-\alpha\right)\left(2-\vartheta\right)}{2}}}\right]+ \\ &F_{\mathrm{m}}\left(\alpha+\frac{1-\alpha}{2}\vartheta\right)\left[l-\frac{1}{2\lambda}\mathrm{ln}\frac{1+\sqrt{\dfrac{\left(1-\alpha\right)\left(2-\vartheta\right)}{2}}}{1-\sqrt{\dfrac{\left(1-\alpha\right)\left(2-\vartheta\right)}{2}}}\right] \end{aligned} $$ (23) 根据s(x)在x=x′t处的连续性，可得锚固系统张拉端位移：
$$ \begin{aligned}[b] & s_0=\frac{D}{6k_{\mathrm{u}}}(x\mathrm{_t}'^3-x_{\mathrm{t}}^3)+ \\ &\qquad\frac{\left(Dx_{\mathrm{t}}'-F\mathrm{_r}\right)x\mathrm{_t^2}-Dx\mathrm{_t}'^2x\mathrm{_t}+2P_0x\mathrm{_t}}{2k\mathrm{_u}}+s\mathrm{_t} \end{aligned} $$ (24) 3.2 指数曲线软化模型
如图8所示，该模型假设当剪切位移大于侧壁弹簧的极限位移st时，其侧阻力开始由极限侧阻力Fm按指数函数进行衰减，在剪切位移达到s′t时衰减至残余侧阻力Fr，其指数函数型式如下：
$$ F\left(x\right)=F\mathrm{_r}e^{\vartheta'\left(x-x\mathrm{_t}'\right)} $$ (25) 式中：ϑ'为指数软化系数，且ϑ'＞0，可根据室内剪切试验或工程经验取值。
根据边界条件可反算获得剪切位移s′t所对应的深度x′t为
$$ x\mathrm{_t}'=x\mathrm{_t}-\frac{1}{\vartheta'}\mathrm{ln}\frac{1}{\alpha} $$ (26) 式中：α定义同前，即
$ \alpha=F\mathrm{_r}/F_{\mathrm{m}} $ 。由此，可将侧阻力分布曲线划分为滑移区、软化区以及弹性变形区，各区内的侧阻力分布函数如下：
$$ F\left(x\right)=\left\{\begin{aligned} & k_{\mathrm{u}}'s\left(x\right) && x_{\mathrm{t}}\le x\le l \\ & F_{\mathrm{r}}e^{\vartheta'\left(x-x_{\mathrm{t}}'\right)} && x\mathrm{_t}'\le x\le x\mathrm{_t} \\ & F_{\mathrm{r}} && 0\le x\le x\mathrm{_t}'\end{aligned}\right. $$ (27) 同理，经推导并代入边界条件后，可得锚固系统的位移分布函数、轴力分布函数以及剪应力分布函数分别为
$$ s\left(x\right)=\left\{\begin{aligned} & \frac{\mathrm{cosh}[\lambda(l-x)]}{\mathrm{cosh}[\lambda(l-x_{\mathrm{t}})]}s\mathrm{_t} & x\mathrm{_t}\le x\le l \\ & \frac{F_r}{\vartheta'^2k\mathrm{_u}}\left[e^{\vartheta'\left(x-x\mathrm{_t}'\right)}-\frac{1}{\alpha}\right]+ \\ & \left(\frac{F\mathrm{_r}x\mathrm{_t}' - P_0}{k_{\mathrm{u}}} - \frac{F_{\mathrm{r}}}{\vartheta'k\mathrm{_u}}\right)\left(x - x\mathrm{_t}\right) + s_{\mathrm{t}} & x_{\mathrm{t}}'\le x\le x_{\mathrm{t}} \\ & \frac{F_{\mathrm{r}}}{2k\mathrm{_u}}x^2-\frac{P_0}{k_{\mathrm{u}}}x+s_0 & 0\le x\le x_{\mathrm{t}}'\end{aligned}\right. $$ (28) $$ P\left(x\right)=\left\{\begin{aligned} & \frac{\mathrm{sinh}[\lambda(l-x)]}{\mathrm{cosh}[\lambda(l-x\mathrm{_t})]}k_{\mathrm{u}}\lambda s\mathrm{_t} & & x\mathrm{_t}\le x\le l \\ & P_0-\frac{F\mathrm{_r}}{\vartheta'}\left[e^{\vartheta'\left(x-x\mathrm{_t}'\right)}-1\right]-F\mathrm{_r}x\mathrm{_t}' & & x\mathrm{_t}'\le x\le x\mathrm{_t} \\ & P_0-F_{\mathrm{r}}x & & 0\le x\le x\mathrm{_t}'\end{aligned}\right. $$ (29) $$ \tau\left(x\right)=\left\{\begin{aligned} & \frac{\mathrm{cosh}[\lambda(l-x)]}{2\text{π}r\mathrm{cosh}[\lambda(l-x_{\mathrm{t}})]}k_{\mathrm{u}}'s\mathrm{_t} && x\mathrm{_t}\le x\le l \\ & \frac{F\mathrm{_r}e^{\vartheta'\left(x-x\mathrm{_t}'\right)}}{2\text{π}r} && x\mathrm{_t}'\le x\le x\mathrm{_t} \\ & \frac{F\mathrm{_r}}{2\text{π}r} && 0\le x\le x\mathrm{_t}'\end{aligned}\right. $$ (30) 根据P(x)在x=xt处的连续性，可得张拉端拉拔力：
$$ P_0=\frac{\mathrm{sinh}[\lambda(l-x\mathrm{_t})]}{\lambda\mathrm{cosh}[\lambda(l-x\mathrm{_t})]}F_{\mathrm{m}}+\frac{F\mathrm{_r}}{\vartheta'}\left(\frac{1}{\alpha}-1\right)+F_{\mathrm{r}}x\mathrm{_t}' $$ (31) 同理，对上式进行求解，即可求得xt。式(31)两边对xt进行求导，并求解xt，即可求得在极限拉拔力P0max下的剪切面的临界破坏深度：
$$ {x}_{\mathrm{t}\mathrm{j}}=l-\frac{1}{2\lambda }\mathrm{ln}\frac{1+\sqrt{1-\alpha }}{1-\sqrt{1-\alpha }} $$ (32) 此时，极限拉拔力为
$$ \begin{aligned}[b] & P_{0\mathrm{max}}=\frac{F\mathrm{_m}}{\lambda}\mathrm{tanh}\left(\frac{1}{2}\mathrm{ln}\frac{1+\sqrt{1-\alpha}}{1-\sqrt{1-\alpha}}\right)+ \\ &\frac{F_{\mathrm{r}}}{\vartheta'}\left(\frac{1}{\alpha}-1\right)+F\mathrm{_r}\left(l-\frac{1}{2\lambda}\mathrm{ln}\frac{1+\sqrt{1-\alpha}}{1-\sqrt{1-\alpha}}\right) \end{aligned} $$ (33) 据s(x)在x=x′t处的连续性，可得张拉端位移：
$$ \begin{aligned}[b] & s_0=\frac{F\mathrm{_m}\left(\alpha-1\right)}{\vartheta'^2k\mathrm{_u}}+\left(\frac{F\mathrm{_r}x\mathrm{_t}'-P_0}{k_{\mathrm{u}}}-\frac{F\mathrm{_r}}{\vartheta'k_{\mathrm{u}}}\right)\left(x\mathrm{_t}'-x\mathrm{_t}\right)- \\ &\frac{F\mathrm{_r}}{2k_{\mathrm{u}}}x_{\mathrm{t}}'^2+\frac{P_0}{k\mathrm{_u}}x\mathrm{_t}'+s_{\mathrm{t}} \end{aligned} $$ (34) 4. 试验验证
为验证上述模型的准确性和适用性，分别采用全长灌浆土层锚索和全长灌浆岩石锚杆的现场抗拔试验实测结果进行对比分析。
4.1 土层锚索的现场拉拔试验
选取“深坪锚索综合试验项目”的A12-a#试验锚索，已知：极限拉拔力P0max=770 kN；锚固长度l=12 m；筋体半径rb=16.5 mm；筋体弹性模量Eb=210 GPa；钻孔半径rg=90 mm；砂浆弹性模量Eg=20 GPa；砂浆泊松比μg=0.25；周边土体的剪切模量Gr=8 MPa。根据现场试验得知，该试验锚索薄弱锚固界面为灌浆体–岩土体界面，且界面剪切模型参数有：极限抗剪强度τm=160 kPa，残余抗剪强度τr=80 kPa。由此，可计算得到锚固界面极限侧阻力Fm=90.5 kN/m，残余侧阻力Fr=45.2 kN/m，系数α=0.5。根据前述参数，可进行以下计算：依据式（11）计算出来的筋体和灌浆体的综合弹性模量Ec=26.4 GPa，由此求得的ku=0.67 GN；文献[4]的假定，锚固系统影响半径取R=35rb，由此按式（14）计算出来的k'u为27.0 MPa，进一步计算得到λ=0.2 m−1，从而可计算得到P0max=663 kN，与实测值较为接近。因此上述参数可用于计算分析。
实际试验中，在P0=210 kN的张拉荷载下锚索锚固界面未出现开裂或破坏，仍处于弹性状态。根据前述分析可知，修正弹簧模型、线性软化模型以及指数曲线软化模型在弹性变形阶段是完全一致的。图9显示了P0=210 kN荷载下（弹性变形阶段）轴力分布预测曲线与实测数据的对比，可以看出两者吻合程度很高。
随着张拉荷载的增加，锚固界面发生塑性软化甚至滑移破坏，根据现场试验可知，在张拉荷载P0=630 kN下试验锚索锚固界面已发生明显的塑性变形，灌浆体应变监测结果显示塑性变形区范围约5 m左右，其中软化段长度约1 m，由此可反算获得该级荷载下的线性软化系数ϑ=0.2及指数软化系数ϑ'=0.7，将软化系数代入各分析模型中进行计算，得到各分析模型在P0=630 kN荷载下（塑性变形阶段）轴力分布预测曲线与实测数据的对比，如图10所示。可以看出，在P0=630 kN荷载下，线性软化模型和指数曲线软化模型的分析结果非常接近，并且与实测数据均非常吻合。相较之下，修正弹簧模型的预测曲线在试验锚索的中下部与实测结果存在一些偏差。
4.2 岩石锚杆的现场拉拔试验
岩石锚杆现场拉拔试验由刘 波等[12]在某山区的岩石基础锚固工程中所做，已知该岩石锚杆参数为：锚杆长度l=3 m；筋体半径rb=21 mm；筋体弹性模量Eb=200 GPa；钻孔半径rg=75 mm；水泥砂浆单轴抗压强度为27.1 MPa，弹性模量Eg=26 GPa。在钢筋上开槽，并间隔150 mm布设了应变片，以监测锚杆应力应变的变化情况。经试验测定并拟合得到筋体–灌浆体界面上的剪切模型参数：st=0.21 mm，s′t=0.38 mm，界面极限抗剪强度τm=3.84 MPa，界面残余抗剪强度τr=1.15 MPa。由此，可反算获得：锚固界面剪切刚度k´u=2.4 GPa，λ=2.95 m−1，极限侧阻力Fm=506.7 kN/m，残余侧阻力Fr=151.7 kN/m，系数α=0.3。
实际试验中在P0=160 kN的张拉荷载下锚杆锚固界面未出现开裂或破坏，仍处于弹性状态。根据前述分析可知，修正弹簧模型、线性软化模型以及指数曲线软化模型在弹性变形阶段是完全一致的。图11显示了P0=160 kN荷载下（弹性变形阶段）锚杆轴力分布预测曲线与实测数据的对比，可以看出两者吻合程度很高。
随着张拉荷载的增加，锚固界面发生塑性软化甚至滑移破坏，试验实测得到：P0=250 kN荷载下锚杆张拉端位移s0=0.43 mm，由此反算得到该级荷载下xt=0.265 m及x′t=0.06 m，进一步可反算获得该级荷载下的线性软化系数ϑ=0.78及指数软化系数ϑ'=5.8，将软化系数分别代入各分析模型中进行分析计算，得到各分析模型在P0=250 kN荷载下（塑性变形阶段）的轴力分布预测曲线与实测数据的对比，如图12所示。
由图12可以看出，在P0=250 kN荷载下，线性软化模型和指数曲线软化模型的分析结果非常接近，且均与实测数据非常吻合。相较之下，修正弹簧模型的预测曲线与实测数据存在较大偏差。
综上所述，考虑锚固界面软化特性能更加真实地反映锚固系统实际的受力变形特性，无论是线性软化还是指数曲线软化，在选取了合适的软化系数的情况下两者的分析结果差异不大。软化系数与锚固界面剪切刚度以及周边岩土体力学性质等有较大的关系，在同种计算模型下，土层锚索与岩石锚杆的软化系数值相差较大。
5. 软化系数敏感性分析
为了解软化系数对全长灌浆锚固系统力学行为的影响，本节利用上述岩石锚杆的拉拔试验相关参数，分别对上述模型的线性软化系数和指数软化系数进行敏感性分析。
5.1 线性软化系数的影响
图13显示了线性软化系数ϑ对极限抗拔力P0max及破坏深度的影响，可以看出：随着ϑ的增加，P0max近乎线性增加，xtj呈非常微弱地增加趋势，而xt和x′t均在逐渐减小，x′t减小的速率更快。
图14显示了不同线性软化系数ϑ下，锚杆在P0=300 kN时的位移、轴力以及剪应力分布曲线。
可以看出：随着ϑ的增大，锚杆各深度处的位移均在减小，距锚杆张拉端越近，位移减小的也越明显，当ϑ由0.1变化至0.5时，张拉端位移也由0.87 mm减小至0.69 mm；随着ϑ的增大，滑移破坏区内锚杆各深度处轴力保持不变，滑移破坏区以下各深度处的轴力逐渐减小，锚杆轴力衰减速率加快，当ϑ由0.1变化至0.5时，0.9 m深度处的轴力也由112.6 kN减小至58.2 kN；随着ϑ的增大，锚固界面的剪应力峰值在逐渐向张拉端推移，软化区范围逐渐增加，而滑移破坏区范围逐渐减小，当ϑ由0.1变化至0.5时，剪切破坏区深度xt由0.76 m减小至0.53 m，软化区起始深度x′t由0.68 m减小至0.27 m。
综上所述，可得出结论：线性软化系数ϑ的变化对锚固系统的拉拔力学行为有较为明显的影响。随着ϑ的增大，塑性变形区以及滑移破坏区范围逐渐减小，而软化区范围在逐渐增加，极限抗拔力近乎线性增加。
5.2 指数软化系数的影响
图15为指数软化系数ϑ'对极限抗拔力P0max及破坏深度的影响，可以看出：随着ϑ'的增加，P0max缓慢地近乎线性减小，xtj维持不变，而xt和x′t均在逐渐增大，x′t增大的速率更快。
图16为不同指数软化系数ϑ'下，锚杆在P0=300 kN时的位移、轴力以及剪应力分布曲线。可以看出：随着ϑ'的增大，锚杆各深度处的位移均在逐渐增加，距锚杆张拉端越近，位移增加的也越明显，当ϑ'由3.0增大至7.0时，张拉端位移也由0.63 mm增加至0.82 mm；随着ϑ'的增大，除张拉端外，锚杆各深度处的轴力也在逐渐减小，锚杆轴力衰减速率变缓，当ϑ'由3.0增大至7.0时，0.9 m深度处的轴力也由47.9 kN增加至90.7 kN；随着ϑ'的增大，锚固界面的剪应力峰值在逐渐向锚杆远端推移，软化区范围逐渐减小，而滑移破坏区范围逐渐增加，当ϑ'由3.0增大至7.0时，剪切破坏区深度xt由0.47 m扩展至0.68 m，软化区起始深度x′t由0.06 m扩展至0.51 m。由此表明，指数软化系数ϑ'的增长对锚杆拉拔力学行为的影响效果与线性软化系数ϑ的增长影响效果相比，刚好是完全相反的两种状态。
综上所述，可得出结论：指数软化系数ϑ'的变化对锚固系统的拉拔力学行为和承载性能有较为明显的影响。随着ϑ'的增大，塑性变形区以及滑移破坏区范围逐渐增加，而软化区范围在逐渐减小，极限抗拔力近乎线性地减小，并且减小幅度非常微弱。
通过对上述软化系数进行敏感性分析可知，锚固界面软化特性对全长灌浆锚固系统的拉拔力学行为有很大的影响，在其力学分析时要合理考虑锚固界面的软化特性以及选取合适的软化系数。
6. 结论
本文依托“深坪锚索综合试验项目”的5条全长灌浆锚索的拉拔试验，对其锚固界面剪切滑移特性进行了分析；基于离散化的思想，将弹簧单元法引入锚固系统力学分析中，建立了位移分布函数、轴力分布函数以及侧阻力分布函数之间的联系；考虑锚固界面的软化特性，假设极限侧阻力分别以线性和指数曲线两种形式衰减至残余摩阻力，模拟锚固界面的软化过程，并分析界面软化特性对锚固系统拉拔力学行为的影响；采用现场拉拔试验进行了验证。研究表明：
（1）锚固界面上的剪切滑移曲线具有以下特征：当剪切位移较小时，剪应力随着剪切位移线性增加；当剪应力达到极值后，随着剪切位移的增加，其值迅速减小；此后，随着剪切位移的进一步增加，其值呈缓慢减小趋势。
（2）弹簧单元法与荷载传递法在本质上是一致的，两者都需要先确定荷载传递函数，相比荷载传递法，弹簧单元法具有更为简洁的形式，便于求解。
（3）考虑锚固界面软化特性能更加真实地反映锚固系统的受力变形特性，无论是线性软化还是指数曲线软化，在选取了合适的软化系数的情况下，两者的分析结果差异很小。软化系数对锚固系统的拉拔力学行为有较明显的影响，在其力学分析时要合理考虑锚固界面的软化特性以及选取合适的软化系数。软化系数与锚固界面剪切刚度以及周边岩土体力学性质等有较大的关系，在同种计算模型下，不同地层条件下的软化系数也不尽相同，在后续的工作中需进一步总结研究。
-
[1] 王卫东, 李永辉, 吴江斌. 超长灌注桩桩–土界面剪切模型及其有限元模拟[J]. 岩土力学,2012,33(12):3818-3824,3832. (WANG W D, LI Y H, WU J B. Pile-soil interface shear model of super long bored pile and its FEM simulation[J]. Rock and Soil Mechanics,2012,33(12):3818-3824,3832. (in Chinese)WANG W D, LI Y H, WU J B. Pile-soil interface shear model of super long bored pile and its FEM simulation[J]. Rock and Soil Mechanics, 2012, 33（12）: 3818-3824,3832. (in Chinese) [2] 曹文贵, 王江营, 翟友成. 考虑残余强度影响的结构面与接触面剪切过程损伤模拟方法[J]. 土木工程学报,2012,45(4):127-133. (CAO W G, WANG J Y, ZHAI Y C. Study of simulation method for the shear deformation of rock structural planes and interfaces with consideration of residual strength[J]. China Civil Engineering Journal,2012,45(4):127-133. (in Chinese)CAO W G, WANG J Y, ZHAI Y C. Study of simulation method for the shear deformation of rock structural planes and interfaces with consideration of residual strength[J]. China Civil Engineering Journal, 2012, 45（4）: 127-133. (in Chinese) [3] 黄明华. 岩土锚杆拉拔荷载传递分析与FRP智能锚杆监测验证[D]. 哈尔滨: 哈尔滨工业大学, 2014. (HUANG M H. Analysis on pullout load transfer mechanism of geotechnical anchor and its validating monitor with smart FRP anchor[D]. Harbin: Harbin Institute of Technology, 2014. (in Chinese)HUANG M H. Analysis on pullout load transfer mechanism of geotechnical anchor and its validating monitor with smart FRP anchor[D]. Harbin: Harbin Institute of Technology, 2014. (in Chinese) [4] CAI Y, ESAKI T, JIANG Y J. A rock bolt and rock mass interaction model[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(7):1055-1067. doi: 10.1016/j.ijrmms.2004.04.005 [5] 尤春安, 战玉宝, 刘秋媛, 等. 预应力锚索锚固段的剪滞–脱黏模型[J]. 岩石力学与工程学报,2013,32(4):800-806. (YOU C A, ZHAN Y B, LIU Q Y, et al. Shear lag-debonding model for anchorage section of prestressed anchor cable[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(4):800-806. (in Chinese) doi: 10.3969/j.issn.1000-6915.2013.04.019YOU C A, ZHAN Y B, LIU Q Y, et al. Shear lag-debonding model for anchorage section of prestressed anchor cable[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32（4）: 800-806. (in Chinese) doi: 10.3969/j.issn.1000-6915.2013.04.019 [6] BENMOKRANE B, CHENNOUF A, MITRI H S. Laboratory evaluation of cement-based grouts and grouted rock anchors[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1995,32(7):633-642. [7] REN F F, YANG Z J, CHEN J F, et al. An analytical analysis of the full-range behaviour of grouted rockbolts based on a tri-linear bond-slip model[J]. Construction and Building Materials,2010,24(3):361-370. doi: 10.1016/j.conbuildmat.2009.08.021 [8] LIU X J, MA Z G. Mechanical behavior analysis of fully grouted bolt under axial load[J]. Scientific Reports,2023,13(1):421. doi: 10.1038/s41598-023-27673-6 [9] MA S Q, ZHAO Z Y, NIE W, et al. An analytical model for fully grouted rockbolts with consideration of the pre- and post-yielding behavior[J]. Rock Mechanics and Rock Engineering,2017,50(11):3019-3028. doi: 10.1007/s00603-017-1272-5 [10] MALVAR L J. Bond of reinforcement under controlled confinement[J]. Materials Journal,1992,89(6):593-601. [11] MOOSAVI M, KHOSRAVI A, JAFARI A. A laboratory study of bond failure mechanism in deformed rock bolts using a modified hoek cell[C]//Proceedings of the ISRM International Symposium - 2nd Asian Rock Mechanics Symposium. Beijing, China: ISRM, 2001. [12] 刘 波, 李东阳, 段艳芳, 等. 锚杆–砂浆界面黏结滑移关系的试验研究与破坏过程解析[J]. 岩石力学与工程学报,2011,30(S1):2790-2797. (LIU B, LI D Y, DUAN Y F, et al. Experimental study of bong-slip relationship between bolt and mortar and theoretical solution to failure process[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(S1):2790-2797. (in Chinese)LIU B, LI D Y, DUAN Y F, et al. Experimental study of bong-slip relationship between bolt and mortar and theoretical solution to failure process[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30（S1）: 2790-2797. (in Chinese) -
下载:
下载:
计量
- 文章访问数: 70
- HTML全文浏览量: 21
- PDF下载量: 16
- 被引次数: 0
