Slump-based soil conditioning of EPB shield in gravelly sand and its prediction study
-
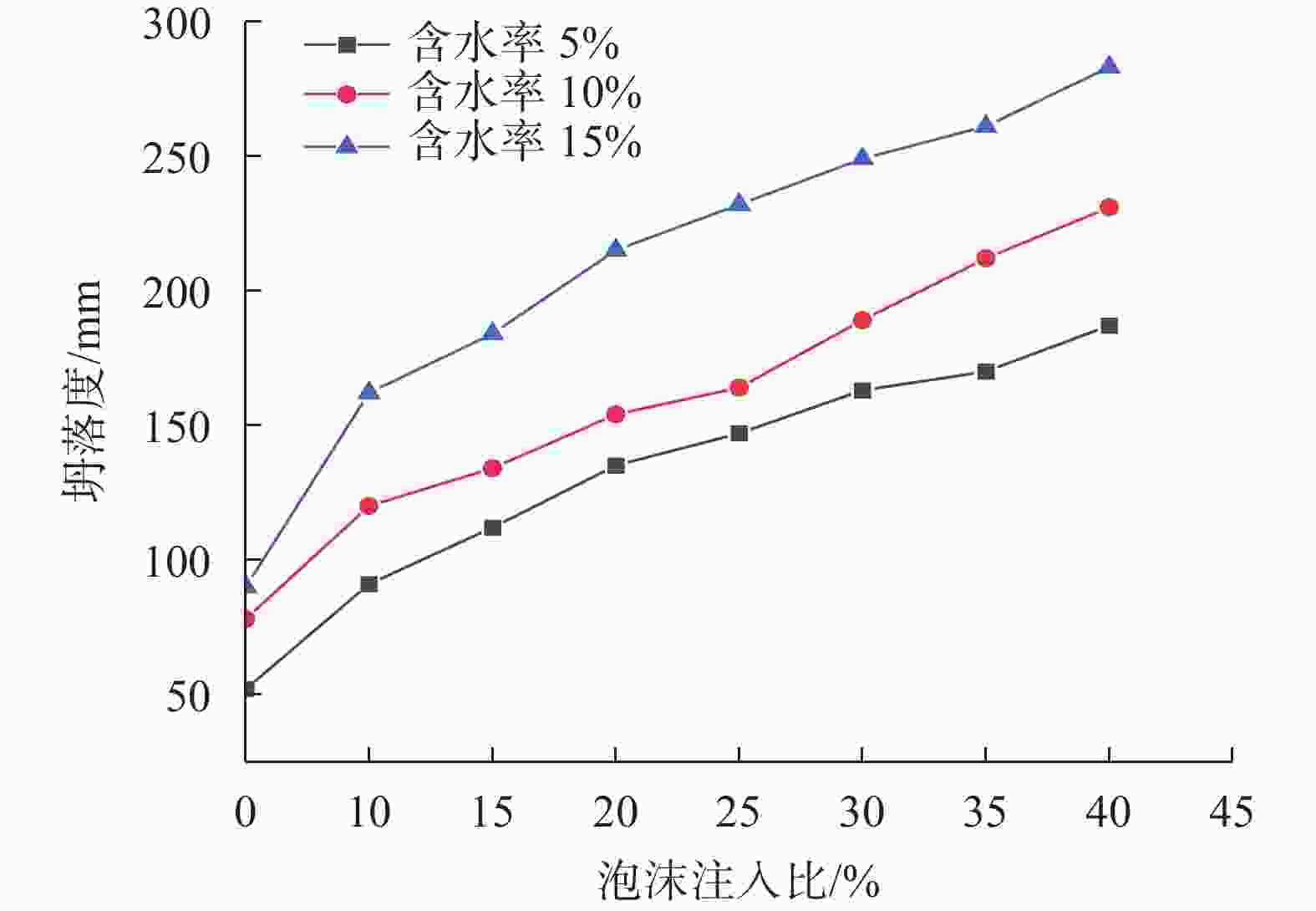
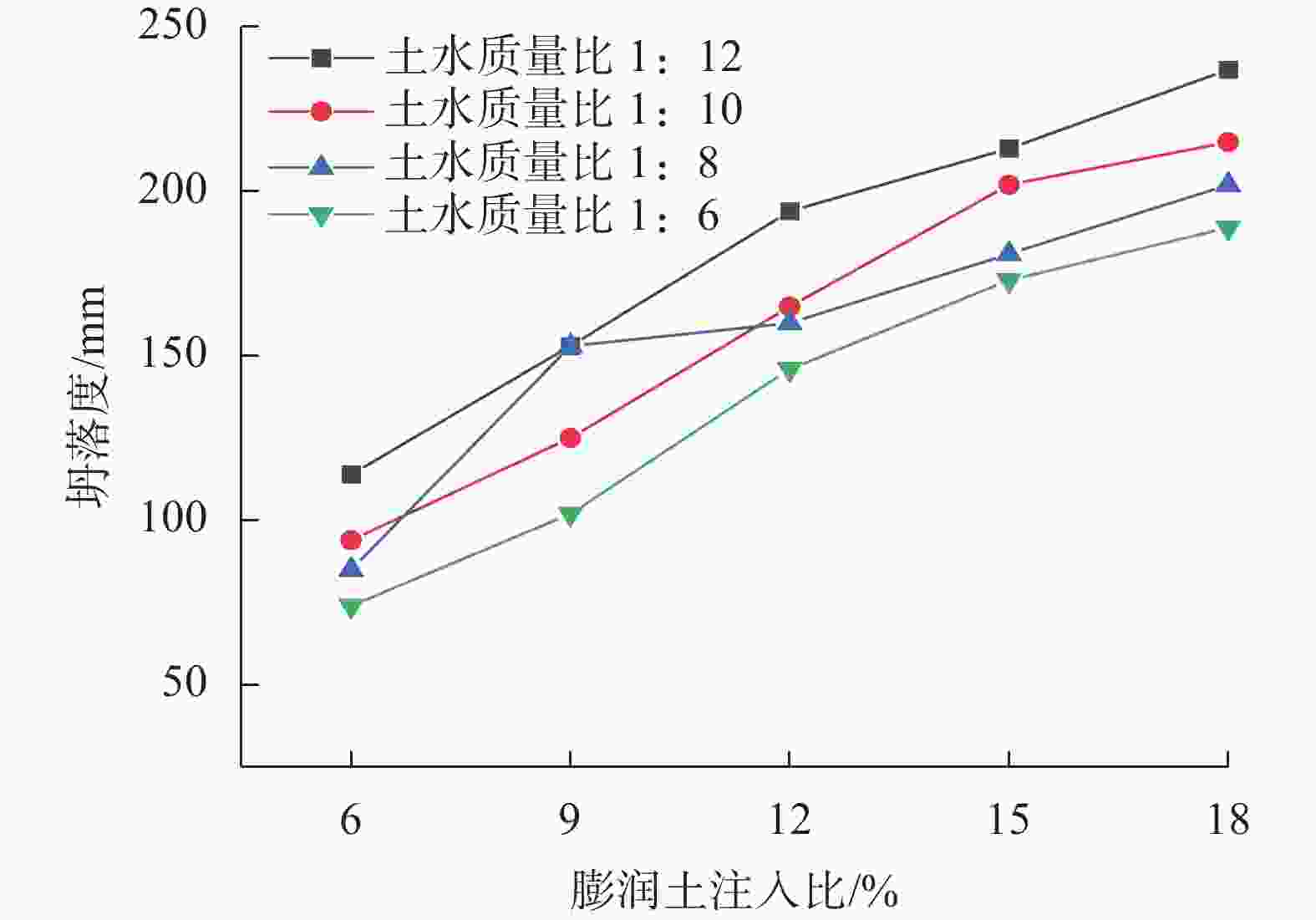
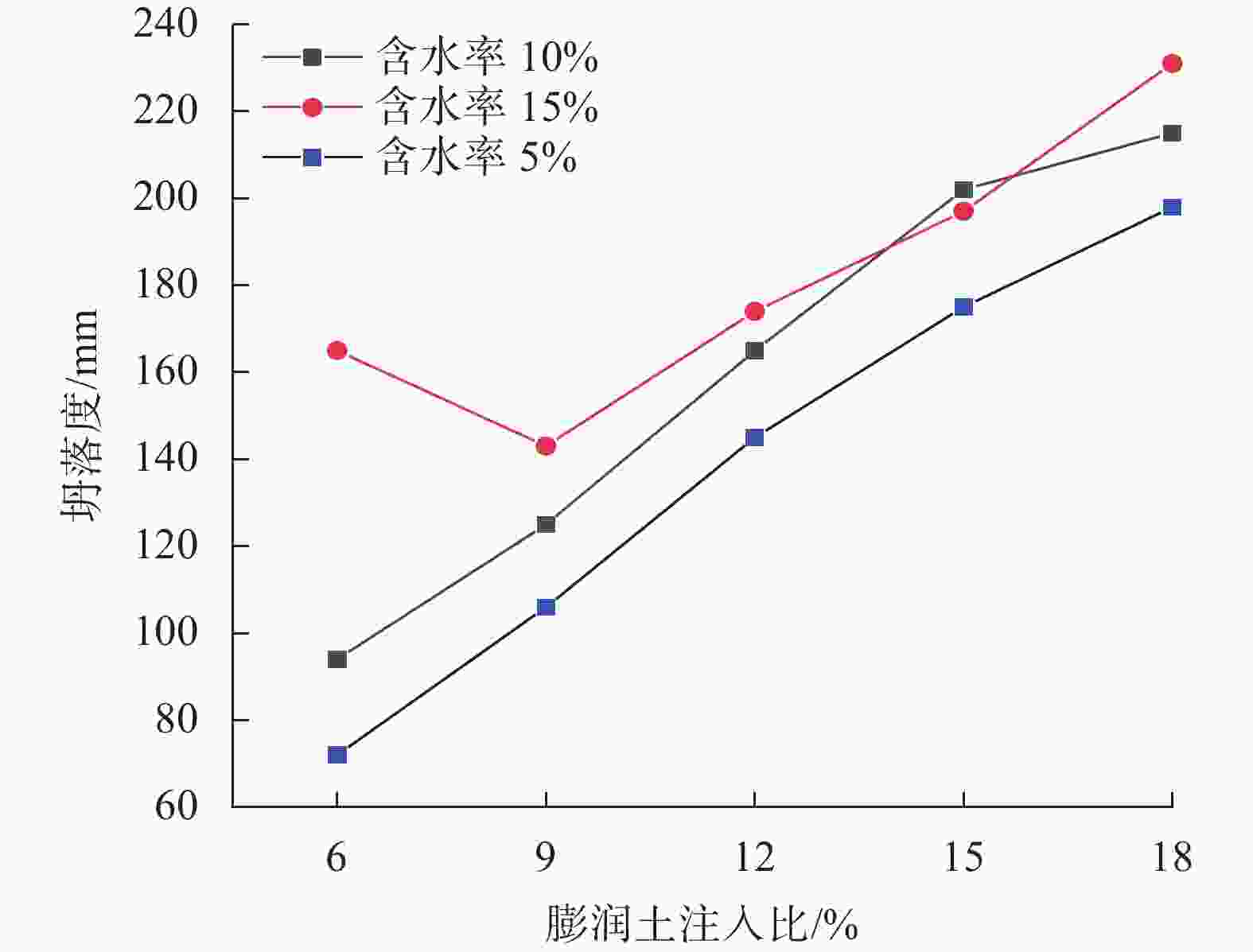
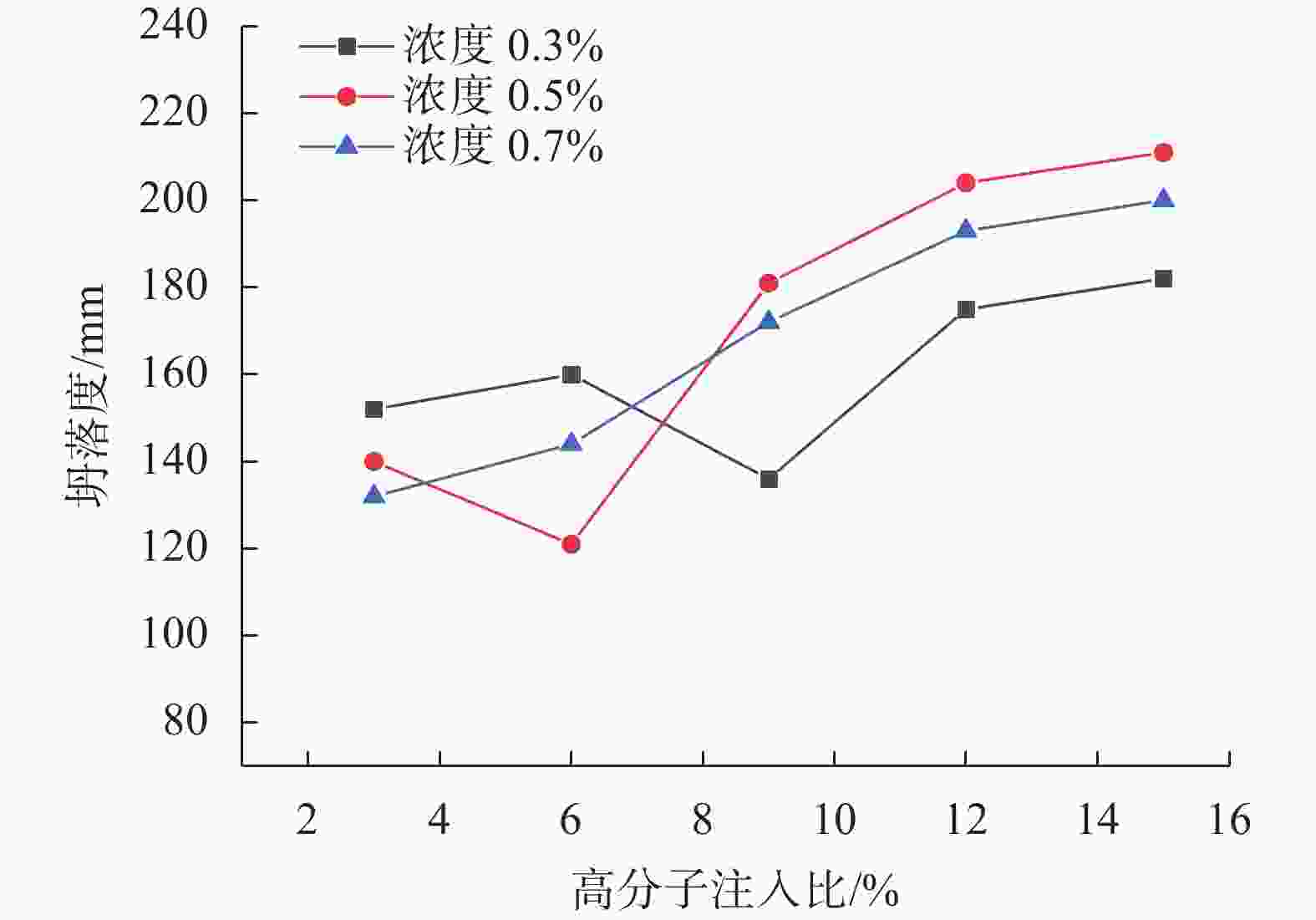
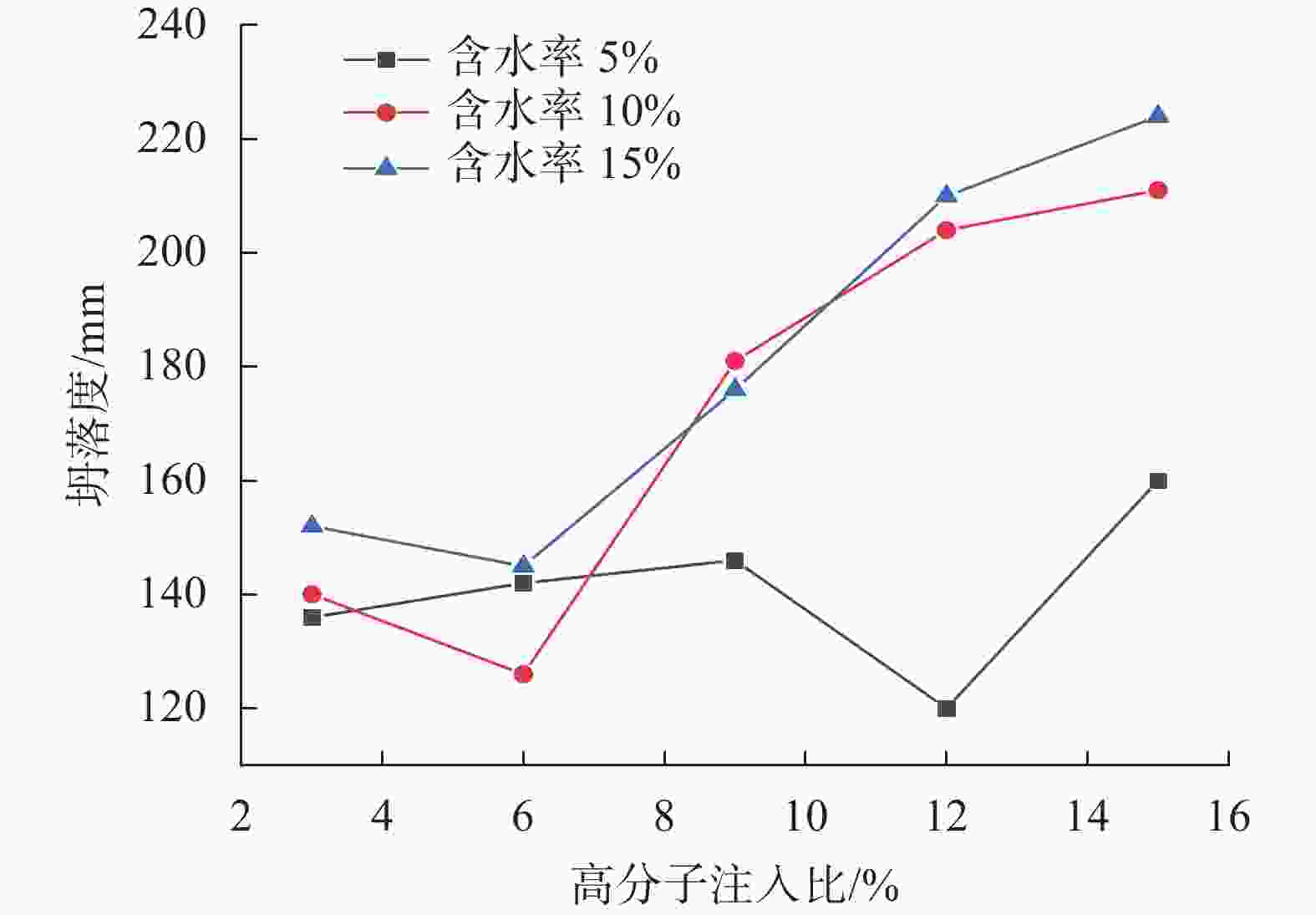
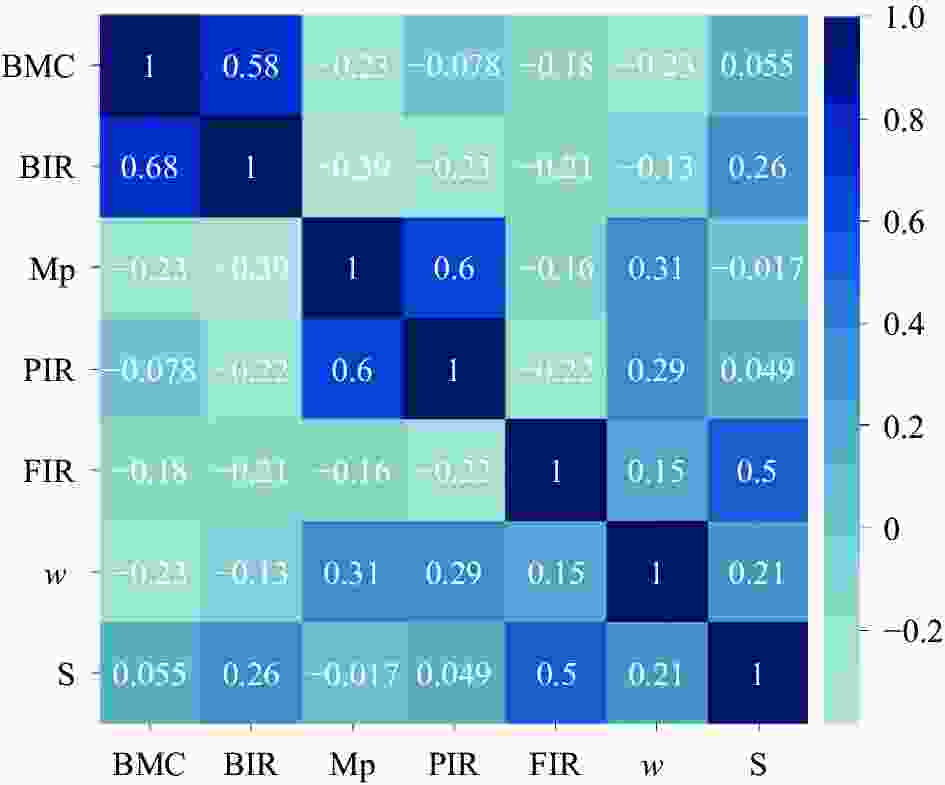
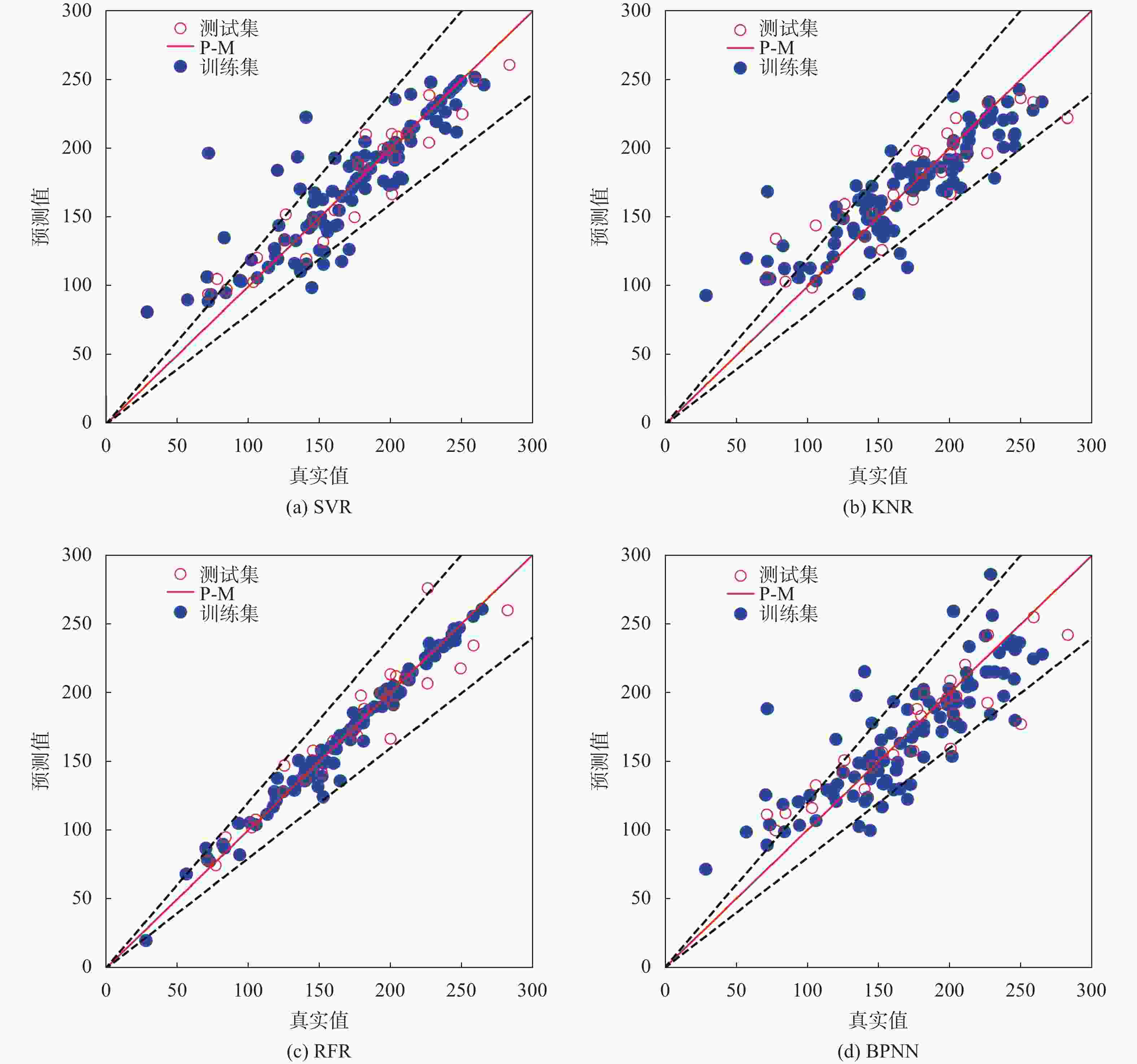
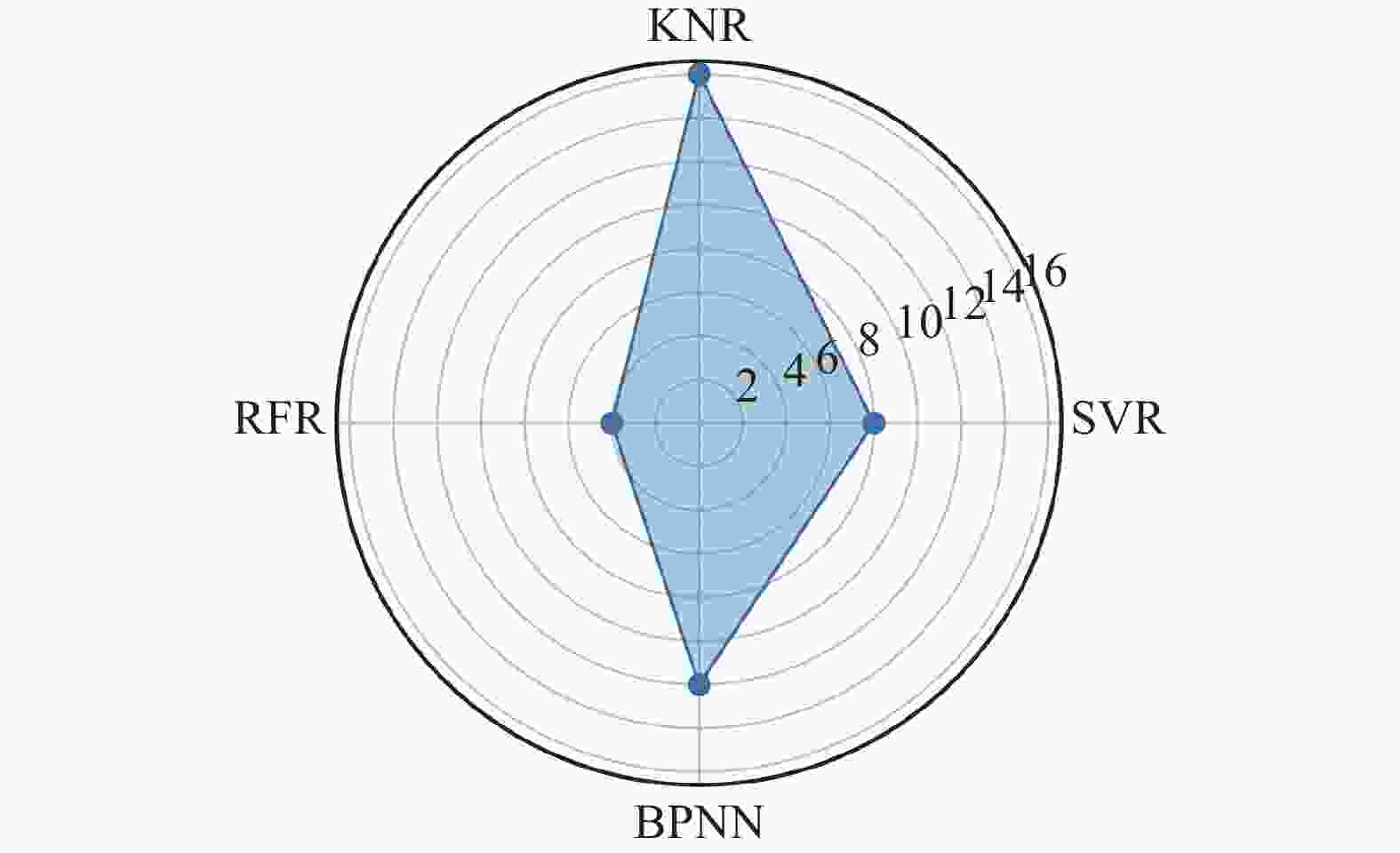
摘要: 在砾砂地层中掘进时，渣土改良效果是影响盾构掘进效率的关键因素。通过坍落度试验研究了泡沫、膨润土泥浆和高分子聚合物对改良土体流塑性的影响。以试验结果作为数据样本集，采用SVR，KNR，RFR和BPNN等常用机器学习方法构建了土体坍落度的预测模型，并将预测值与实际值进行了对比分析。研究结果表明：（1）泡沫对砾砂渣土流塑性的改良效果较好；（2）对于高含水率的砾砂地层，应使用高黏度的膨润土泥浆或PAM溶液进行改良，以起到保水增黏、防止喷涌的目的；（3）对比SVR，KNR和BPNN模型，RFR模型在预测时的性能表现最佳，能够更准确地预测改良渣土的坍落度，并且对模型进行了可解释性分析。Abstract: The impact of soil conditioning is a critical factor influencing shield tunneling efficiency in strata of gravelly sand. Through a slump test, the impacts of foam, bentonite slurry, and polymer on the enhanced soil’s flow plasticity were examined. A prediction model of soil slump was provided using machine learning techniques like SVR, KNR, RFR, and BPNN, utilizing the test results as the data sample set. The predicted and real values were then compared and examined. The study indicates that: (1) Foam has a greater impact on enhancing the gravelly sandy soil’s flow flexibility. (2) High-viscosity bentonite slurry or PAM solution should be applied over gravelly sandy stratum with high water content to retain water, improve viscosity, and prevent blowout. (3) The RFR model outperforms the SVR, KNR, and BPNN models regarding prediction accuracy. It can also forecast the slump of the improved waste soil with greater precision. The model’s interpretability was examined as well.
-
0. 引言
近年来城市轨道交通快速发展，土压平衡盾构施工广泛应用于各大城市的地铁隧道建设[1]。盾构在砾砂地层中掘进时，由于砾砂的孔隙率大、颗粒分散、黏聚性极低、渗透性较高，施工过程中易出现喷涌、开挖面失稳、沉降过大等问题[2−4]。在此类地层盾构施工时，渣土改良效果的好坏，直接影响盾构的掘进的效率及安全性[5−6]。
为确保盾构机可以顺利开挖，压力稳定，国内外学者在土压平衡盾构渣土改良机制和改良剂选取等方面开展了大量研究。魏康林[7]总结出改良良好的渣土应具有较低的渗透性，较小的内摩擦角，一定的黏聚力，良好的压缩性，以及一定的流塑性。汪国锋[8]初步建立了渣土改良的评价体系，提出了改良效果的计算公式。对于高渗透性、低黏聚性的砾砂地层，常采用泡沫剂、膨润土泥浆、高分子聚合物进行改良。徐琳琳等[9]对富水砂层进行渣土改良研究，结果表明同时使用泡沫和膨润土泥浆能够有效改良渣土的流塑性并降低刀盘扭矩。乔国刚等[10]对富水粗砂地层进行坍落度、渗透性、压缩性、剪切强度等改良试验，指出泡沫可以显著降低土体的内摩擦角，提升压缩性。胡长明等[11]使用钙基、钠基膨润土对砂土地层进行改良，研究表明钠基膨润土土水质量比达到1∶10时，注入比为20%可以有效降低刀盘磨损及刀具表面温度。郭付军等[12]选用三种典型聚合物对砂土地层进行室内试验，结果表明PAM性价比高，改良效果好，使用浓度为0.3%的聚合物注入比为20%～25%可以显著增强粗砂的流塑性和黏性。
目前对于砾砂地层中土体改良材料的选用和配比缺乏理论指导，现场多以试错的方式，根据施工经验来尝试改良剂的掺量，经常造成不必要的成本支出及施工风险。本文采用泡沫、膨润土、高分子聚合物对砾砂地层进行渣土改良，通过坍落度试验研究了泡沫、膨润土泥浆、高分子聚合物的浓度与注入比对改良土体流塑性的影响，同时使用SVR，KNR，RFR，BPNN四种机器学习模型对渣土改良后的土体的流塑性进行预测，为富水砾砂地层盾构渣土改良提供一种新的效果评价途径，最后通过可解释性分析，分析了所建立的RFR预测模型及其决策过程。
1. 砾砂渣土改良的坍落度试验
1.1 砾砂地层颗粒级配分析
采用筛分法对现场取回原状土进行颗粒级配试验。如图1所示，土层中的砾石含量较高，粒径处于2～20 mm的砾砂比例高达31.61%，粒径20 mm以上的占比为24.92%，处于0.075～2 mm之间的砂石含量占比约为43.14%。粒径小于0.075 mm的细微颗粒占比只有0.33%，不足1%。土体平均粒径为3.42 mm，为典型砾砂地层。通过颗粒筛分试验结果计算得出，地层不均匀系数Cu为19.92（C u≥5），表明级配不均匀；曲率系数Cc为0.27，位于区间1~3之外，亦表明为级配不良（见表1）。
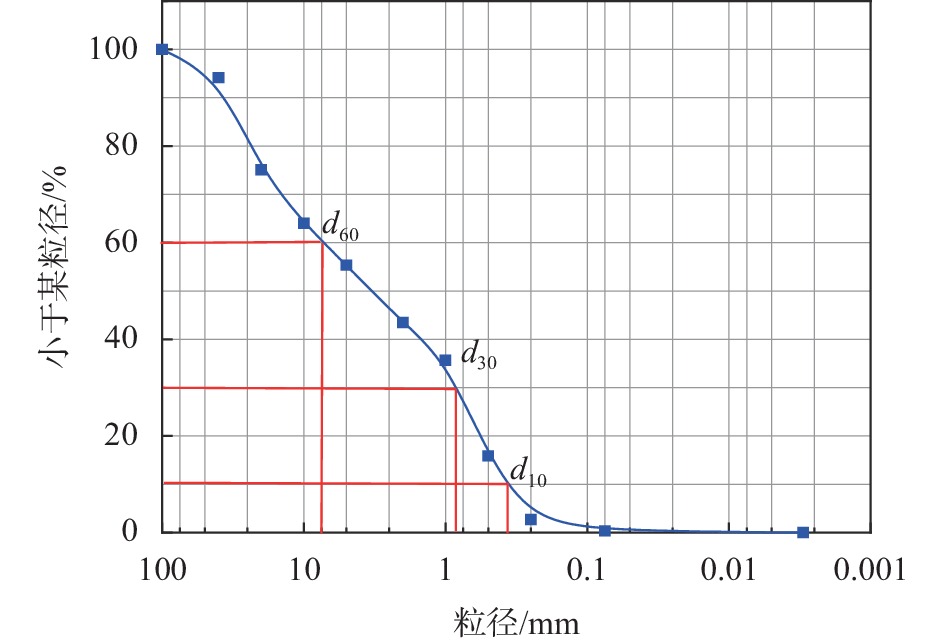
表 1 砾砂地层颗粒组成指标有效粒径d10/mm 平均粒径d50/mm 限制粒径d60/mm 不均匀系数Cu 曲率系数
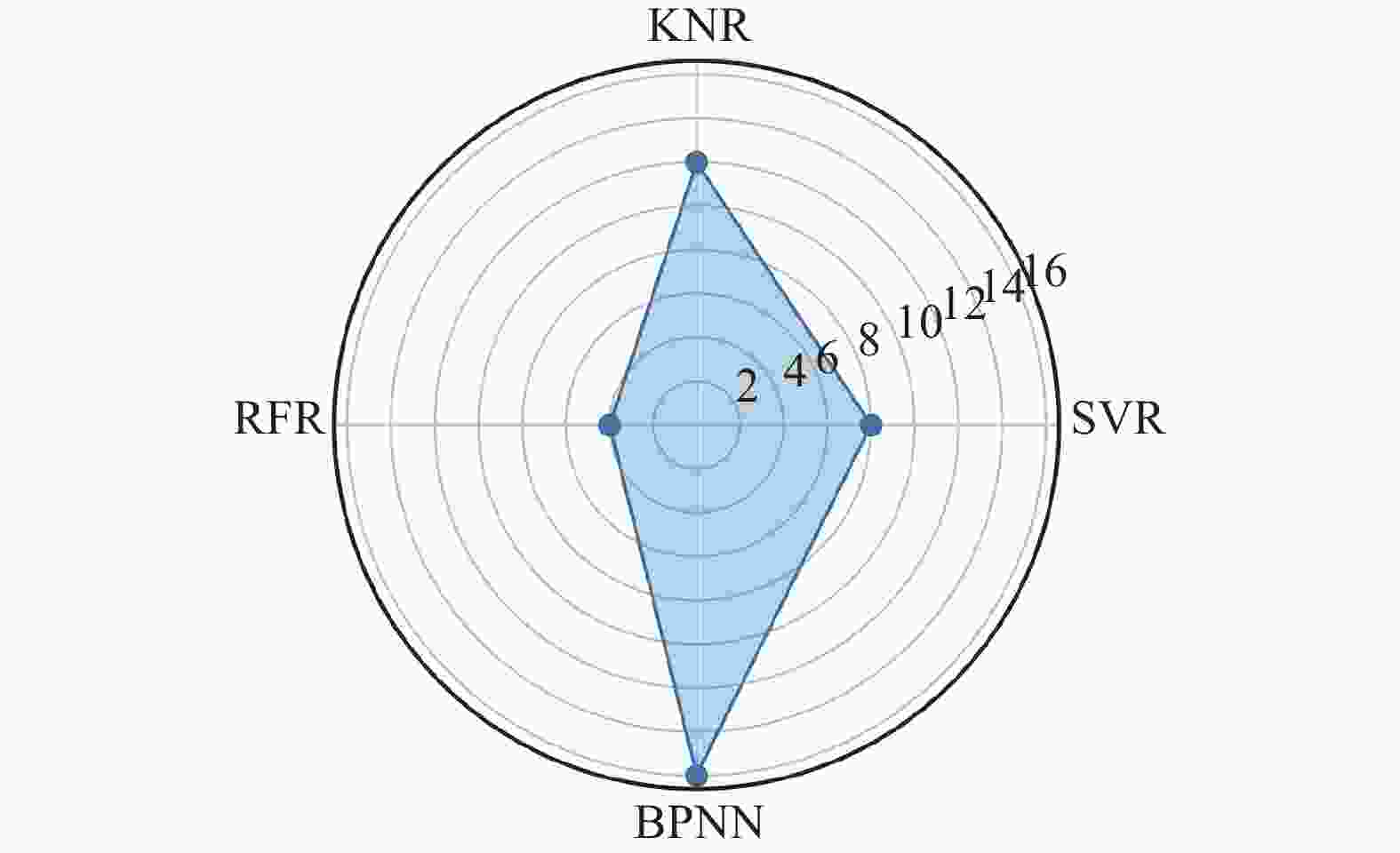
Cc0.37 3.42 7.37 19.92 0.27 1.2 泡沫对砾砂渣土流塑性改良
配置好浓度为3%的泡沫，使用发泡机发泡制备，泡沫注入比（简称FIR）按10%~30%，以5%为梯度逐一加入到渣土中进行坍落度试验。FIR按式（1）进行计算。
$$ \mathrm{F}\mathrm{I}\mathrm{R}=\frac{V_{\mathrm{f}}}{V\mathrm{_m}}\times100\% $$ (1) 式中：
$ {V}_{\mathrm{f}} $ 为注入的泡沫体积，L；$ V_{\mathrm{m}} $ 为土体体积，L。由图2可知，泡沫对土体坍落度的增加有较好的效果。含水率为10%的渣土泡沫注入比从0%增加到40%，坍落度从78 mm增长到231 mm，流动性的改良效果显著。随着泡沫注入比的增加，渣土的坍落度也随之增加。但泡沫注入比不易过高，泡沫注入比过高，析泡沫现象严重，影响改良效果。泡沫的坍落度也与土体的含水率有关。土体的含水率越大，渣土的坍落度也就越大。对于含水率15%的土体，泡沫注入比10%，土体坍落度为162 mm，即满足室内试验的要求，但有水析出；泡沫注入比为20%的情况下，含水率从5%提升到10%，坍落度从135 mm上升到154 mm，坍落度明显上升且流动性较好，但含水率至15%时，坍落度激增到215 mm，析水现象明显。
1.3 膨润土泥浆对砾砂渣土流塑性改良
按质量比例配置好1∶6，1∶8，1∶10，1∶12的膨润土泥浆，泥浆注入比（Bentonite Injection Ratio，简称BIR）从6%提升至18%，以3%为梯度依次做坍落度试验，然后配置含水率为5%，10%，15%的土体，使用浓度为1∶10的膨润土做坍落度试验，分析含水率对泥浆注入比改变坍落度的影响。如图3所示，渣土的坍落度随泥浆注入比的增加而升高。但随泥浆浓度的增大，泥浆黏度增加，渣土塑性随之增强，坍落度随膨润土水质量比的增加而减小。泥浆土水质量比较小时，坍落度增长速率快，说明渣土中水含量对其有影响。
膨润土泥浆土水质量比为1∶10时，不同含水率坍落度随泥浆注入比的变化规律如图4所示。对含水率较高的情况，泥浆注入比较低时，土体呈现松散状态，无塑性，黏度微弱，此时坍落度为165 mm；随着泥浆注入比的增加，土体黏度增加，坍落度先降低后升高，在注入比为9%的情况下出现拐点。整体来看，含水率15%的土体，坍落度从数值上看比含水率10%的坍落度高，但改良效果差，析水现象严重。
1.4 高分子聚合物对砾砂渣土流塑性改良
使用不同浓度的高分子聚合物溶液对10%含水率的土体进行改良，结果如图5所示。随着高分子注入比（Polymer Injection Ratio，简称PIR）的增加，溶液浓度低时，坍落度先减小后增大，浓度为0.3%和0.5%的溶液随注入比的增大分别在注入比为10%和6%的情况下出现拐点。在拐点之后，高分子对土体的改良才能起到较好的效果，拐点随着浓度的增大向左移动。
为分析含水率对高分子改良土体的影响，使用浓度为0.5%的PAM溶液对含水率5%，10%，15%的土体进行改良。由图6可知，在含水率较低时，高分子溶液对土体的改良效果极差，土体失水严重，颗粒松散较干，产生劈裂现象。含水在10%以上时，高分子溶液相同注入比下，含水率对坍落度的影响差异不大，但是随着含水率的升高，土体析水现象明显，由此可知对于含水率更大的地层，应使用高浓度的PAM溶液进行改良，才能起到保水增黏的作用。
2. 基于机器学习的砾砂地层盾构渣土流塑性预测
2.1 机器学习模型
采用4种常用机器学习方法构建土体坍落度的预测模型，具体如下：
（1）Support Vector Regression （简称SVR）模型。SVR模型通过利用支持向量机的思想来解决回归问题[13]。SVR使用一组训练样本，通过在训练样本中寻找一个边界，使得预测值与真实值之间的误差最小化，可以根据输入的特征预测出相应的连续输出。它可以处理非线性、高维以及具有噪音的数据。
（2）K-Nearest Neighbors Regression （简称KNR）模型。如果一个样本的K个最近邻的输出类似，那么该样本的输出也应该类似。通过计算输入样本与训练集中所有样本之间的距离，找到与输入样本最接近的K个训练样本，然后通过这K个样本的输出值来预测输入样本的输出[14]。
（3）Random Forest Regression （简称RFR）模型。RFR将多个决策树组合成一个强大的模型，通过取决于多个决策树的预测平均值来进行回归[15]。随机森林在构建每个决策树时使用了随机采样和随机特征选择，以增加模型的多样性和减少过拟合的风险，具有良好的鲁棒性和预测能力，适用于处理高维数据和特征相关性较强的问题。
（4）Back-Propagation Neural Network （BPNN）模型。BPNN由多个神经元层组成，其中每个神经元通过反向传播算法进行训练[16]。BPNN使用前向传播将输入信号传递到输出层，然后根据输出与目标之间的误差来调整网络中的权重和偏置，最小化误差。BPNN适用于复杂的非线性问题，并且可以通过添加隐藏层来提高模型的复杂度和性能。
2.2 评价指标
分别采用决定系数（R2）、均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）评价各预测模型的准确性。
（1）决定系数（R2）。R2的好处在于其结果进行归一化，更容易看出模型间的差，R2越大越好。当我们预测的模型完全准确时，R2等于最大值1；当R2<0时，说明模型还不如基准模型，很可能数据不存在任何线性关系。决定系数可按式（2）进行计算。
$$ \mathit{\mathrm{\mathit{R}}}^2=1-\frac{\displaystyle\sum_i^{ }(\hat{y}_i-y_i)^2}{\displaystyle\sum_i^{ }(\overline{y}_i-y_i)^2} $$ (2) 式中：
$ {y}_{i} $ 是真实值；$ {\overline{y}}_{i} $ 是均值；$ \hat y_{i} $ 是对应的预测值。（2）均方误差（MSE）。MSE是用于衡量预测值与真实值之间的平均差异的指标。其公式如式（3）所示。
$$ \mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{m}\sum _{1}^{m}(\hat y_{i}-{y}_{i}{)}^{2} $$ (3) 式中：m是样本数量；
$ {y}_{i} $ 是真实值；$ \hat y_{i} $ 是对应的预测值。（3）均方根误差（RMSE）。RMSE是MSE的平方根，可以告诉我们预测值与真实值之间的平均误差。和MSE具有相同的单位，其公式如式（4）所示。
$$ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{m}\sum _{1}^{m}(\hat y_{i}-{y}_{i}{)}^{2}} $$ (4) （4）平均绝对误差（MAE）。MAE是衡量预测值与真实值之间平均绝对差异的指标，MAE越小，表示模型的预测越准确，其公式如式（5）所示。
$$ \mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{m}\sum _{i=1}^{m}\left|\hat y_{i}-{y}_{i}\right| $$ (5) 2.3 SHAP可解释性模型
SHAP（SHapley Additive exPlanations）[17−18]是一个用于解释机器学习模型预测结果的Python包。它基于合作博弈论的概念，为每个特征分配一个“贡献值”，以解释模型对每个样本的预测结果。换句话说，SHAP值表示了每个特征对于模型预测值的影响程度，帮助理解模型是如何基于不同特征进行预测的。通过分析SHAP值，可以识别出哪些特征对于模型的预测起到了重要作用，从而更好地理解模型的决策过程，如公式（6）所示。
$$ {y}_{i}={y}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}+f\left({x}_{i1}\right)+f\left({x}_{i2}\right)+\dots +f\left({x}_{ik}\right) $$ (6) 式中：
$ {x}_{ik} $ 为第i个样本的第k个特征；$ {y}_{i} $ 为模型对该样本的预测值；$ {y}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}} $ 为所有样本目标变量的均值。2.4 预测结果分析
选取试验过程中的泡沫注入比FIR、膨润土BIR、膨润土浓度BMC、高分子注入比PIR、高分子浓度Mp和含水率w、塌落度S等指标，进行相关系数分析，产生相关矩阵热图。图7为各个类别指标与坍落度的相关关系。可以看出，坍落度与泡沫注入比等上述指标呈现相关关系；泡沫注入比FIR、膨润土注入比BIR、含水率w对改良渣土塌落度的影响位居前三分别为0.50，0.26和0.21。
利用SVR，KNR，RFR和BPNN等常用机器学习方法构建了土体坍落度的预测模型。数据在构建模型之前经过归一化处理，以减少维度差异对结果的影响[18]。同时将20%的数据分为测试集，80%的数据分为训练集进行模型的训练。图8显示了使用4个机器学习模型进行坍落度预测的训练集和测试集的散点图。SVR，KNR和BPNN模型在y=0.8x和y=1.2x处的两条虚线之外都有大量的点，说明模型的性能很差。RFR模型预测值和实测值的训练集基本集中在P-M线和y=0.8x和y=1.2x处的两条虚线上，说明模型拟合效果较好。且预测的S接近P-M线，在训练集和测试集之间的各项评价指标都没有特别的差异，表明RFR的预测的准确率较高。
测试集中四个机器学习模型的预测结果如表2及图9所示。与其他三种模型相比，RFR模型的R2值最大，为0.9025，MSE，RMSE和MAE值分别为287.22，16.947，12.300，在所有模型中最低，表明其在预测改良渣土的塌落度方面具有较好的性能。其余三种模型SVR，KNR，BPNN的R2值较大，且MSE，RMSE和MAE值都高于RFR模型，效果不佳。
训练集中四个机器学习模型的预测结果如表3及图10所示。与其他三种模型相比，RFR模型的R2值最大，MSE，RMSE和MAE值最低，表明其在预测改良渣土的塌落度方面具有较好的性能。SVR模型的准确率R2很高，为89.9%，相比较于测试集的75.55%差别很大，且其余三个模型指标都很高，表明SVR模型在预测时的泛化能力很差。其余KNR，BPNN模型的R2值远低于RFR，而MSE，RMSE和MAE的值都很大，模型预测的效果不佳。
表 2 四种模型的测试集评价指标及排名测试集 R2 排名 MSE
/mm2排名 RMSE
/mm排名 MAE
/mm排名 汇总 SVR 0.75554 2 597.75 2 24.449 2 15.226 2 8 KNR 0.75402 3 601.45 3 24.524 3 18.041 3 12 RFR 0.90255 1 287.22 1 16.947 1 12.300 1 4 BPNN 0.68028 4 781.76 4 27.960 4 20.833 4 16 表 3 四种模型的训练集评价指标及排名训练集 R2 排名 MSE
/mm2排名 RMSE
/mm排名 MAE
/mm排名 汇总 SVR 0.89994 2 294.92 2 17.173 2 14.192 2 8 KNR 0.78865 4 622.95 4 24.959 4 119.665 4 16 RFR 0.92914 1 50.991 1 7.1408 1 4.8726 1 4 BPNN 0.79995 3 589.64 3 24.282 3 18.257 3 12 图11为经过训练的RFR模型的SHAP特征重要度图，以平均Shapley绝对值衡量SHAP特征重要性。FIR特征对模型预测的影响程度为25.73，对于模型的预测有着较大的正向影响，对最终的预测结果起着重要作用。BIR特征对模型预测的影响程度为22，同样也有着较大的正向影响，对最终的预测结果也具有重要作用。w，Mp，PIR 和BMC相较于FIR和BIR特征，影响程度较小，但仍对模型预测有一定的正向影响。
图12为SHAP摘要图，展示了模型特征重要度和特征的影响。FIR对模型预测的正向和负向影响都很大，且在整体上呈现正相关关系。这表明FIR在预测塌落度时起着重要作用，无论是对预测结果的提升还是降低都有显著影响。BMC在SHAP值小于0的区域有较多红色点的分布，表明较大的BMC值会降低对塌落度的预测值。这表明BMC特征在某些情况下可能会对塌落度的预测产生负向影响，特别是在BMC较大时。
3. 结论
本文使用泡沫、膨润土泥浆和PAM对不同含水率的砾砂进行改良，以坍落度作为衡量改良效果的标准，分析了含水率和注入比等因素对改良效果的影响规律。得出的结论如下：
（1）泡沫对砾砂渣土流塑性的改良效果较好，对于含水率为10%的砾砂渣土，泡沫注入比从0%增加到40%时，坍落度从78 mm增长到231 mm。
（2）3种改良方案均受到含水率的影响，对于高含水率的砾砂地层，应使用高黏度的膨润土泥浆或PAM溶液进行改良，以起到保水增黏、防止喷涌的目的。
（3）RFR模型能够有效预测改良渣土的坍落度。对比SVR，KNR和BPNN模型，RFR模型在预测时的性能表现最佳，能够更准确地预测改良渣土的坍落度，并且通过SHAP进行了模型的可解释性分析。
-
表 2 四种模型的测试集评价指标及排名
测试集 R2 排名 MSE
/mm2排名 RMSE
/mm排名 MAE
/mm排名 汇总 SVR 0.75554 2 597.75 2 24.449 2 15.226 2 8 KNR 0.75402 3 601.45 3 24.524 3 18.041 3 12 RFR 0.90255 1 287.22 1 16.947 1 12.300 1 4 BPNN 0.68028 4 781.76 4 27.960 4 20.833 4 16 
下载: 导出CSV
表 3 四种模型的训练集评价指标及排名
训练集 R2 排名 MSE
/mm2排名 RMSE
/mm排名 MAE
/mm排名 汇总 SVR 0.89994 2 294.92 2 17.173 2 14.192 2 8 KNR 0.78865 4 622.95 4 24.959 4 119.665 4 16 RFR 0.92914 1 50.991 1 7.1408 1 4.8726 1 4 BPNN 0.79995 3 589.64 3 24.282 3 18.257 3 12
下载: 导出CSV
-
[1] 胡长明, 张延杰, 谭 博, 等. 富水砂卵石地层土压平衡盾构隧道碴土改良试验研究[J]. 现代隧道技术,2017,54(6):45-55. (HU C M, ZHANG Y J, TAN B, et al. Soil conditioning experiments for EPB shield tunneling in water-rich sandy cobble strata[J]. Modern Tunnelling Technology,2017,54(6):45-55. (in Chinese)HU C M, ZHANG Y J, TAN B, et al. Soil conditioning experiments for EPB shield tunneling in water-rich sandy cobble strata[J]. Modern Tunnelling Technology, 2017, 54（6）: 45-55. (in Chinese) [2] 茅 华. 隧道施工盾构螺旋机喷涌应对措施[J]. 铁道建筑,2014(10):39-41. (MAO H. Countermeasures to stop muck-gushing from shield’s screw conveyer during tunnel construction[J]. Railway Engineering,2014(10):39-41. (in Chinese) doi: 10.3969/j.issn.1003-1995.2014.10.10MAO H. Countermeasures to stop muck-gushing from shield’s screw conveyer during tunnel construction[J]. Railway Engineering, 2014（10）: 39-41. (in Chinese) doi: 10.3969/j.issn.1003-1995.2014.10.10 [3] 王洪新. 土压平衡盾构刀盘扭矩计算及其与盾构施工参数关系研究[J]. 土木工程学报,2009,42(9):109-113. (WANG H X. Calculation of cutterhead torque for EPB shield and the relationship between cutterhead torque and shield driving parameters[J]. China Civil Engineering Journal,2009,42(9):109-113. (in Chinese) doi: 10.3321/j.issn:1000-131X.2009.09.016WANG H X. Calculation of cutterhead torque for EPB shield and the relationship between cutterhead torque and shield driving parameters[J]. China Civil Engineering Journal, 2009, 42（9）: 109-113. (in Chinese) doi: 10.3321/j.issn:1000-131X.2009.09.016 [4] 肖 超, 阳军生, 王树英, 等. 土压平衡盾构改良渣土力学行为及其地层响应特征[J]. 中南大学学报(自然科学版),2016,47(7):2432-2440. (XIAO C, YANG J S, WANG S Y, et al. Conditioned soils mechanical behavior of earth pressure balance shield tunneling and its impact on formation response[J]. Journal of Central South University (Science and Technology),2016,47(7):2432-2440. (in Chinese)XIAO C, YANG J S, WANG S Y, et al. Conditioned soils mechanical behavior of earth pressure balance shield tunneling and its impact on formation response[J]. Journal of Central South University (Science and Technology), 2016, 47（7）: 2432-2440. (in Chinese) [5] MARTINELLI D, PEILA D, CAMPA E. Feasibility study of tar sands conditioning for earth pressure balance tunnelling[J]. Journal of Rock Mechanics and Geotechnical Engineering,2015,7(6):684-690. doi: 10.1016/j.jrmge.2015.09.002 [6] BORIO L, PEILA D. Study of the permeability of foam conditioned soils with laboratory tests[J]. American Journal of Environmental Sciences,2010,6(4):365-370. doi: 10.3844/ajessp.2010.365.370 [7] 魏康林. 土压平衡盾构施工中泡沫和膨润土改良土体的微观机理分析[J]. 现代隧道技术,2007,44(1):73-77. (WEI K L. Micro-mechanism analysis for the soil improvement by foam and bentonite in EPB shield tunneling[J]. Modern Tunnelling Technology,2007,44(1):73-77. (in Chinese) doi: 10.3969/j.issn.1009-6582.2007.01.016WEI K L. Micro-mechanism analysis for the soil improvement by foam and bentonite in EPB shield tunneling[J]. Modern Tunnelling Technology, 2007, 44（1）: 73-77. (in Chinese) doi: 10.3969/j.issn.1009-6582.2007.01.016 [8] 汪国锋. 北京砂卵石地层土压平衡盾构土体改良技术试验研究[D]. 北京: 中国地质大学(北京), 2011. (WANG G F. Tset research on soil improvement technology for EPBS in Beijing sandy pebble stratum[D]. Beijing: China University of Geosciences (Beijing), 2011. (in Chinese)WANG G F. Tset research on soil improvement technology for EPBS in Beijing sandy pebble stratum[D]. Beijing: China University of Geosciences (Beijing), 2011. (in Chinese) [9] 徐琳琳, 余 金, 蒋亚龙, 等. 泡沫性能测试及其在富水砂层渣土改良中应用[J]. 地下空间与工程学报,2021,17(S1):345-353. (XU L L, YU J, JIANG Y L, et al. Testing of foam properties and its application in soil conditioning for water bearing sandy grounds[J]. Chinese Journal of Underground Space and Engineering,2021,17(S1):345-353. (in Chinese)XU L L, YU J, JIANG Y L, et al. Testing of foam properties and its application in soil conditioning for water bearing sandy grounds[J]. Chinese Journal of Underground Space and Engineering, 2021, 17（S1）: 345-353. (in Chinese) [10] 乔国刚, 陶龙光, 刘 波, 等. 泡沫改良富水砂层工程性质的实验研究[J]. 现代隧道技术,2009,46(6):79-84. (QIAO G G, TAO L G, LIU B, et al. Study on engineering properties of foam-conditioned water-soaked sand strata[J]. Modern Tunnelling Technology,2009,46(6):79-84. (in Chinese) doi: 10.3969/j.issn.1009-6582.2009.06.013QIAO G G, TAO L G, LIU B, et al. Study on engineering properties of foam-conditioned water-soaked sand strata[J]. Modern Tunnelling Technology, 2009, 46（6）: 79-84. (in Chinese) doi: 10.3969/j.issn.1009-6582.2009.06.013 [11] 胡长明, 崔 耀, 王雪艳, 等. 土压平衡盾构施工穿越砂层渣土改良试验研究[J]. 西安建筑科技大学学报(自然科学版),2013,45(6):761-766. (HU C M, CUI Y, WANG X Y, et al. Soil improvement for earth pressure balance shields construction in full section sand layer[J]. Journal of Xi’an University of Architecture and Technology (Natural Science Edition),2013,45(6):761-766. (in Chinese)HU C M, CUI Y, WANG X Y, et al. Soil improvement for earth pressure balance shields construction in full section sand layer[J]. Journal of Xi’an University of Architecture and Technology (Natural Science Edition), 2013, 45（6）: 761-766. (in Chinese) [12] 郭付军, 赵振威, 张 杰, 等. 使用聚合物对纯砂层进行渣土改良的试验研究[J]. 隧道建设,2017,37(S1):53-58. (GUO F J, ZHAO Z W, ZHANG J, et al. Experimental study of ground conditioning of pure sand stratum by using polymer[J]. Tunnel Construction,2017,37(S1):53-58. (in Chinese) doi: 10.3973/j.issn.1672-741X.2017.S1.009GUO F J, ZHAO Z W, ZHANG J, et al. Experimental study of ground conditioning of pure sand stratum by using polymer[J]. Tunnel Construction, 2017, 37（S1）: 53-58. (in Chinese) doi: 10.3973/j.issn.1672-741X.2017.S1.009 [13] VAPNIK V, GOLOWICH S E, SMOLA A. Support vector method for function approximation, regression estimation and signal processing[C]//Proceedings of the 10th International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 1996: 281-287. [14] FIX E, HODGES J L. Discriminatory analysis. Nonparametric discrimination: consistency properties[J]. International Statistical Review/Revue Internationale de Statistique,1989,57(3):238-247. [15] BREIMAN L. Random forests[J]. Machine Learning,2001,45(1):5-32. doi: 10.1023/A:1010933404324 [16] ESONYE C, ONUKWULI O D, OFOEFULE A U, et al. Multi-input multi-output (MIMO) ANN and Nelder-Mead’s simplex based modeling of engine performance and combustion emission characteristics of biodiesel-diesel blend in CI diesel engine[J]. Applied Thermal Engineering,2019,151:100-114. doi: 10.1016/j.applthermaleng.2019.01.101 [17] LUNDBERG S M, LEE S I. A unified approach to interpreting model predictions[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Red Hook: Curran Associates, 2017: 4768-4777. [18] ZHANG A, LIPTON Z C, LI M, et al. Dive into deep learning[M]. Cambridge: Cambridge University Press, 2023. -
下载:
计量
- 文章访问数: 43
- HTML全文浏览量: 11
- PDF下载量: 5
- 被引次数: 0
