Precision Analysis and Applications of Trigonometric Leveling with Total Station
-
摘要: 通过介绍双次对向观测法、中间设站观测法、单向双觇标（棱镜）三角高程测量法等测量方法，对全站仪三角高程测量方法的基本原理和精度进行了讨论。通过分析实际应用中的相关问题，认为影响以上观测方法高差测量精度的主要因素为天顶距的大小及其观测误差、大气垂直折光系数测定的误差，仪器高和目标高的量测误差亦是影响因素之一，测距误差的影响则较小。全站仪三角高程测量法可在城市和工程测量中广泛应用。Abstract: The basic principle and accuracy of total station trigonometric leveling method are discussed by introducing the measurement methods such as reciprocal leveling, intermediate station observation and one-way double targets (prism) trigonometric leveling. By analyzing the relevant problems in practical application, it is considered that the main factors affecting the height difference measurement accuracy of the above methods are the size of zenith distance and its observation error, the error of atmospheric vertical refraction coefficient measurement. The measurement error of instrument height and target height is also one of the influencing factors, and the influence of ranging error is slight. Total station trigonometric leveling method can be widely used in urban and engineering surveying.
-
Key words:
- total station /
- trigonometric leveling /
- precision ananysis
-
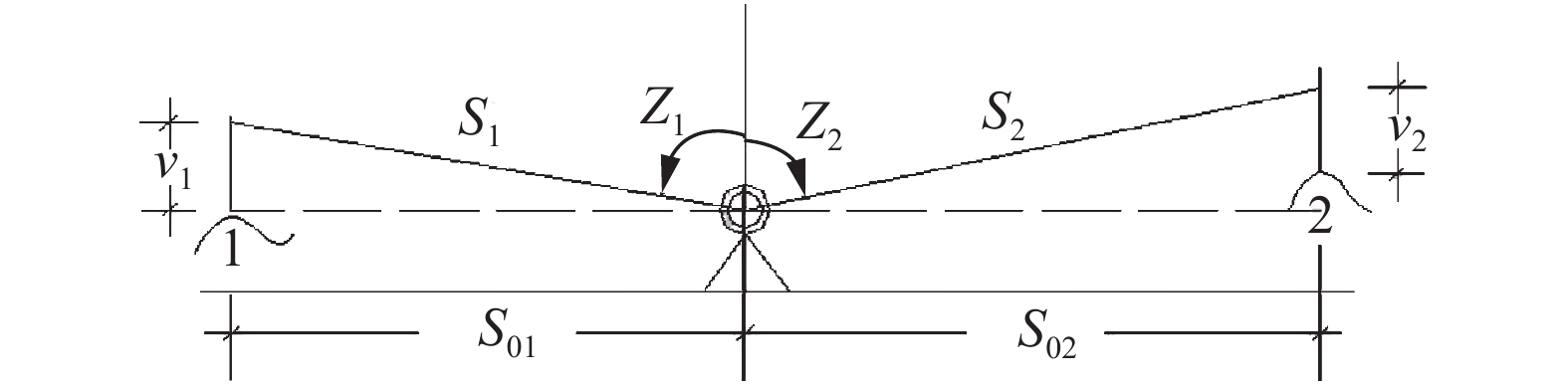
表 1 按式（6）—式（8）以不同斜距估算的测段双次对向观测高差精度一览表
斜距/中差 M2/mm2 S=100 m S=200 m S=300 m S=400 m S=500 m S=1000 m 右边第1项 0.11748 0.46991 1.01402 1.87963 2.93692 11.74769 右边第2项 0.00041 0.00049 0.00058 0.00067 0.00077 0.00137 右边第3项 0.00154 0.02460 0.12455 0.39365 0.96106 15.37692 右边第4、5项之和 1.0(0.25) ${m}_{\rm{h} }^{ {\text{AB} } }$ ±0.75(±0.43) ±0.86(±0.61) ±1.03(±0.83) ±1.28(±1.12) ±1.56(±1.44) ±3.75(±3.70) ${m}_{\rm{hkm} }^{ {\text{AB} } }$ ±2.37(±1.36) ±1.92(±1.36) ±1.88(±1.52) ±2.02(±1.77) ±2.21(±2.04) ±3.75(±3.70) 注：表中括弧内的数值为${m_{\rm{{\rm{i}}} } } = {m_{\rm{v} } } = \pm 0.5\;{\rm{mm} }$的估算值。 
下载: 导出CSV
表 2 不同斜距和不同天顶距双次对向观测的每千米高差中误差一览表
S/m ${M_{ {\rm{hkm} } } }/{\rm{mm} }$ 89° 87° 85° 80° 75° 70° 65° 60° 100 2.37 2.37 2.38 2.39 2.44 2.49 2.55 2.67 200 1.92 1.92 1.93 1.94 1.96 2.00 2.07 2.11 300 1.92 1.92 1.92 1.91 1.91 1.94 1.96 2.00 350 1.96 1.96 1.95 1.96 1.96 1.97 1.99 2.00 400 2.02 2.02 2.03 2.02 2.03 2.02 2.03 2.04 500 2.21 2.21 2.21 2.21 2.20 2.19 2.17 2.16 800 3.04 3.04 3.04 3.01 2.97 2.91 2.84 2.78 1000 3.75 3.75 3.74 3.70 3.63 3.55 3.43 3.31
下载: 导出CSV
表 3 不同斜距和不同天顶距的中间往返观测法的每千米高差中误差一览表
S/m ${M}_{\rm{hkm} }/{\rm{mm} }$ 89° 87° 85° 80° 75° 70° 65° 60° 100 1.10 1.10 1.10 1.17 1.25 1.36 1.50 1.66 200 1.55 1.55 1.55 1.58 1.61 1.65 1.69 1.77 300 1.94 1.94 1.94 1.94 1.96 1.96 1.98 2.00 350 2.28 2.28 2.27 2.28 2.28 2.26 2.27 2.26 400 2.28 2.28 2.27 2.28 2.28 2.26 2.27 2.26 500 2.62 2.61 2.61 2.61 2.58 2.57 2.54 2.53 800 3.65 3.65 3.64 3.62 3.57 3.51 3.45 3.36 1000 4.41 4.41 4.40 4.36 4.31 4.21 4.10 3.97
下载: 导出CSV
表 4 按式（18）以不同斜距估算的单向双觇标法测量的高差精度一览表
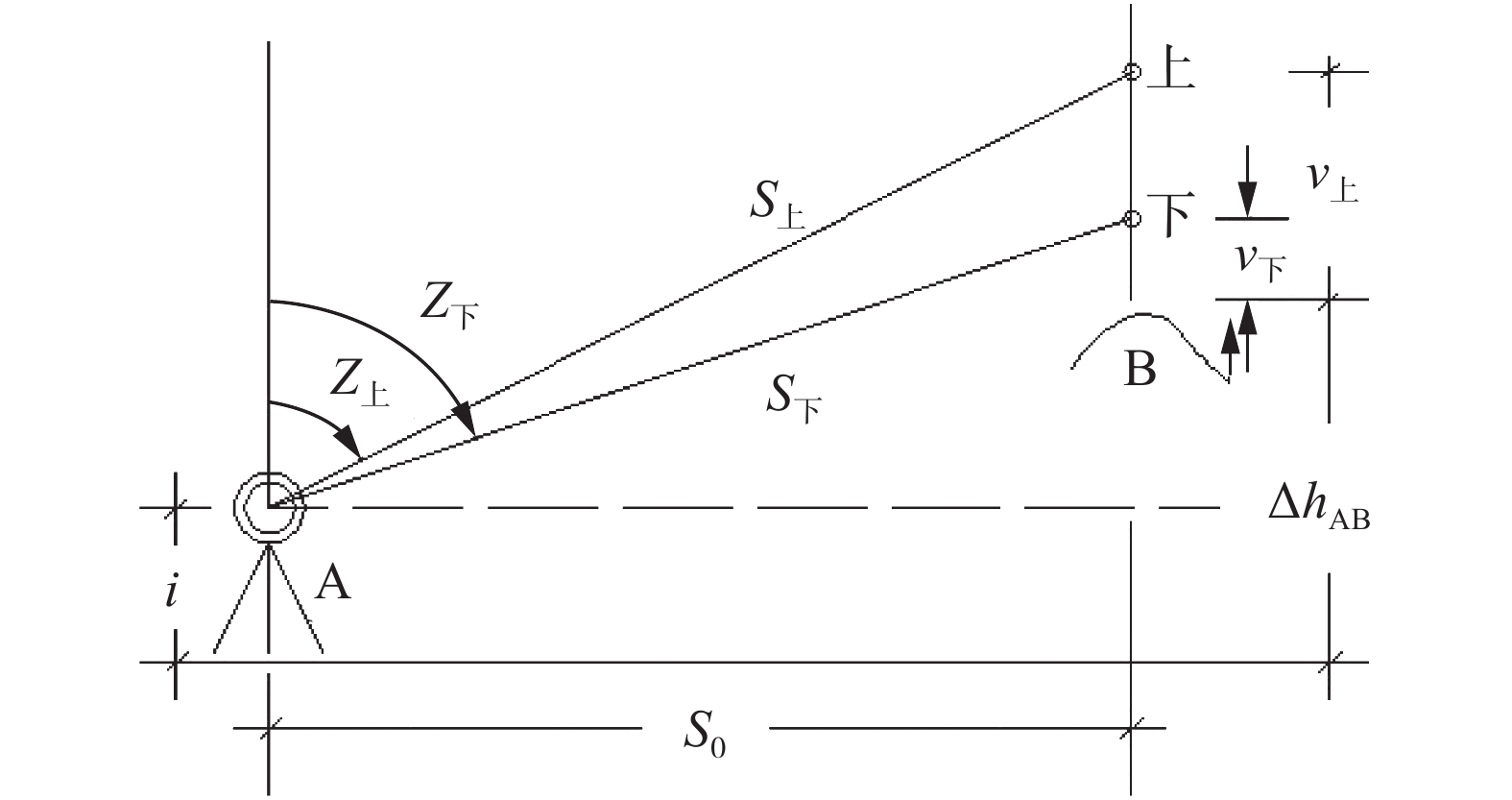
斜距/中差 Mi2/mm2 S斜=100 m S斜=200 m S斜=300 m S斜=400 m S斜=500 m 右边第1项 0.23488 0.93953 2.11394 3.75812 5.87207 右边第2项 0.00083 0.00099 0.00116 0.00134 0.00154 右边第3项 0.00154 0.02460 0.12455 0.39365 0.96106 右边第4项 0.38 mk12 /mm ±0.79 ±1.16 ±1.62 ±2.13 ±2.69
下载: 导出CSV
-
[1] GB 50026—2007 工程测量规范[S]. [2] CJJ/T 8—2011 城市测量规范[S]. [3] JGJ 8—2016 建筑变形测量规范[S]. [4] 郑汉球. 电磁波测距三角高程测量[M].北京: 地质出版社, 1993. [5] 刘志德, 章书寿, 郑汉球, 等. EDM三角高程测量[M].北京: 测绘出版社, 1996. [6] 张基石,曾志元. 高山地区垂线偏差对三角高程的影响[J]. 测绘通报,1985,(2):46-47. [7] 徐正扬,段定乾,杨述魁. 测距三角高程作跨越障碍水准测量的研究[J]. 解放军测绘学院学报,1988,(1):3-12. [8] 余代俊. 全站仪中间法代替二等水准测量的精度分析与实验[J]. 测绘与空间地理信息,2006,(5):117-120. doi: 10.3969/j.issn.1672-5867.2006.05.034 [9] 张亚勇,卢金涛. 二等跨河水准测量在城市轨道交通工程中的应用实例分析[J]. 铁道勘察,2008,(3):29-30. doi: 10.3969/j.issn.1672-7479.2008.03.010 -
图(3) / 表(4)
计量
- 文章访问数: 372
- HTML全文浏览量: 114
- PDF下载量: 72
- 被引次数: 0
