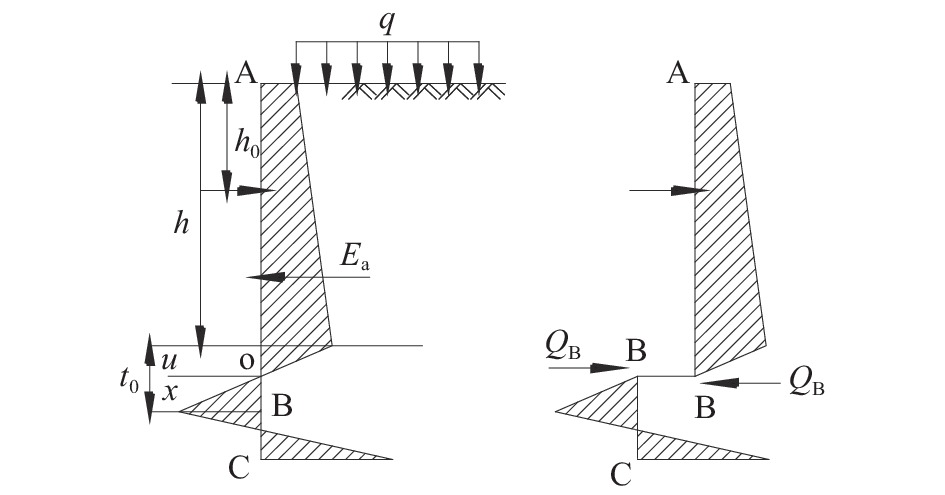
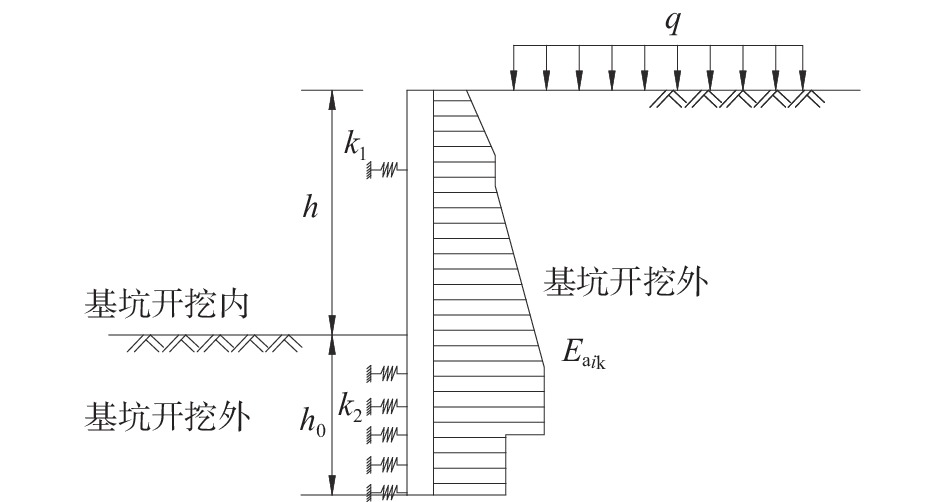
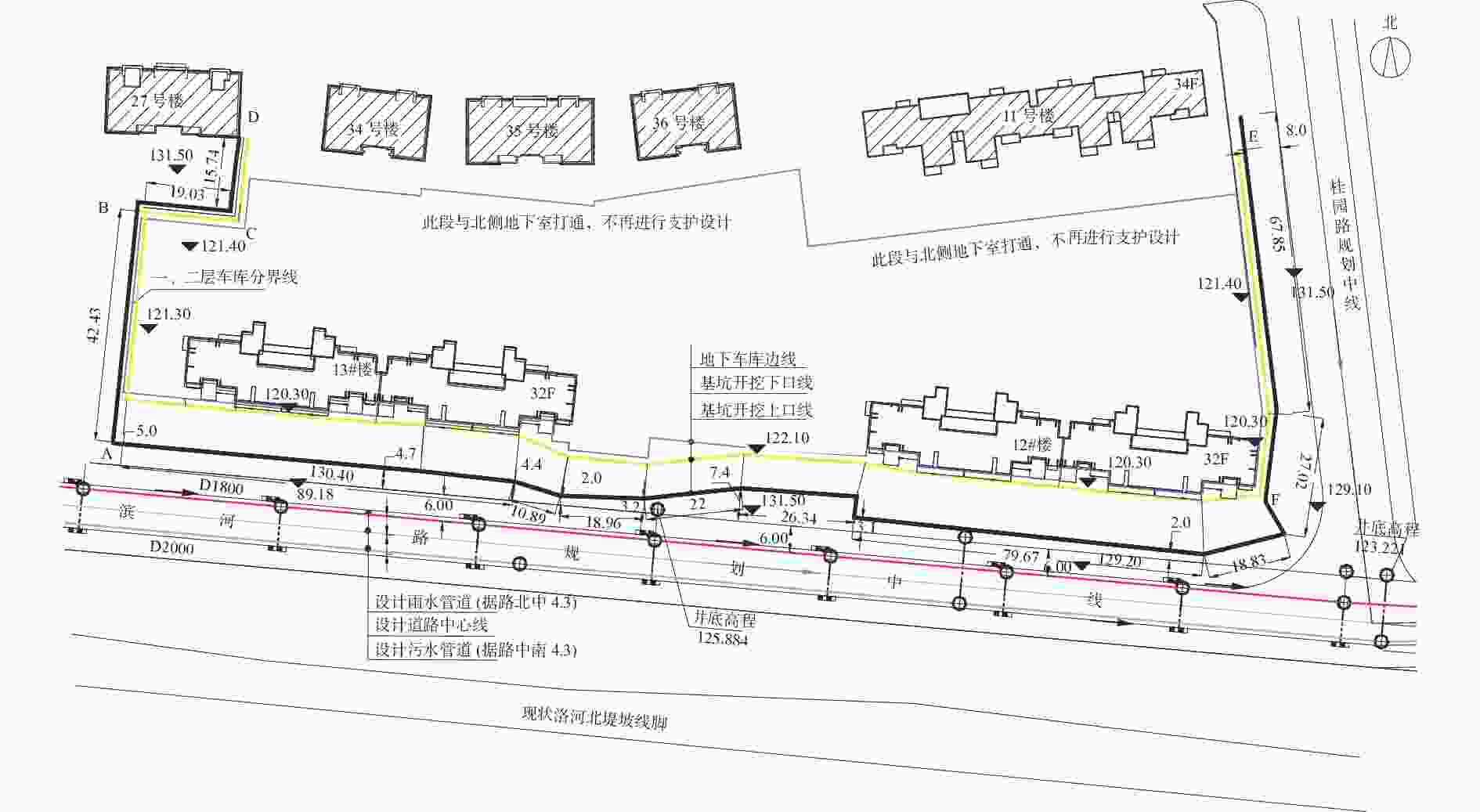
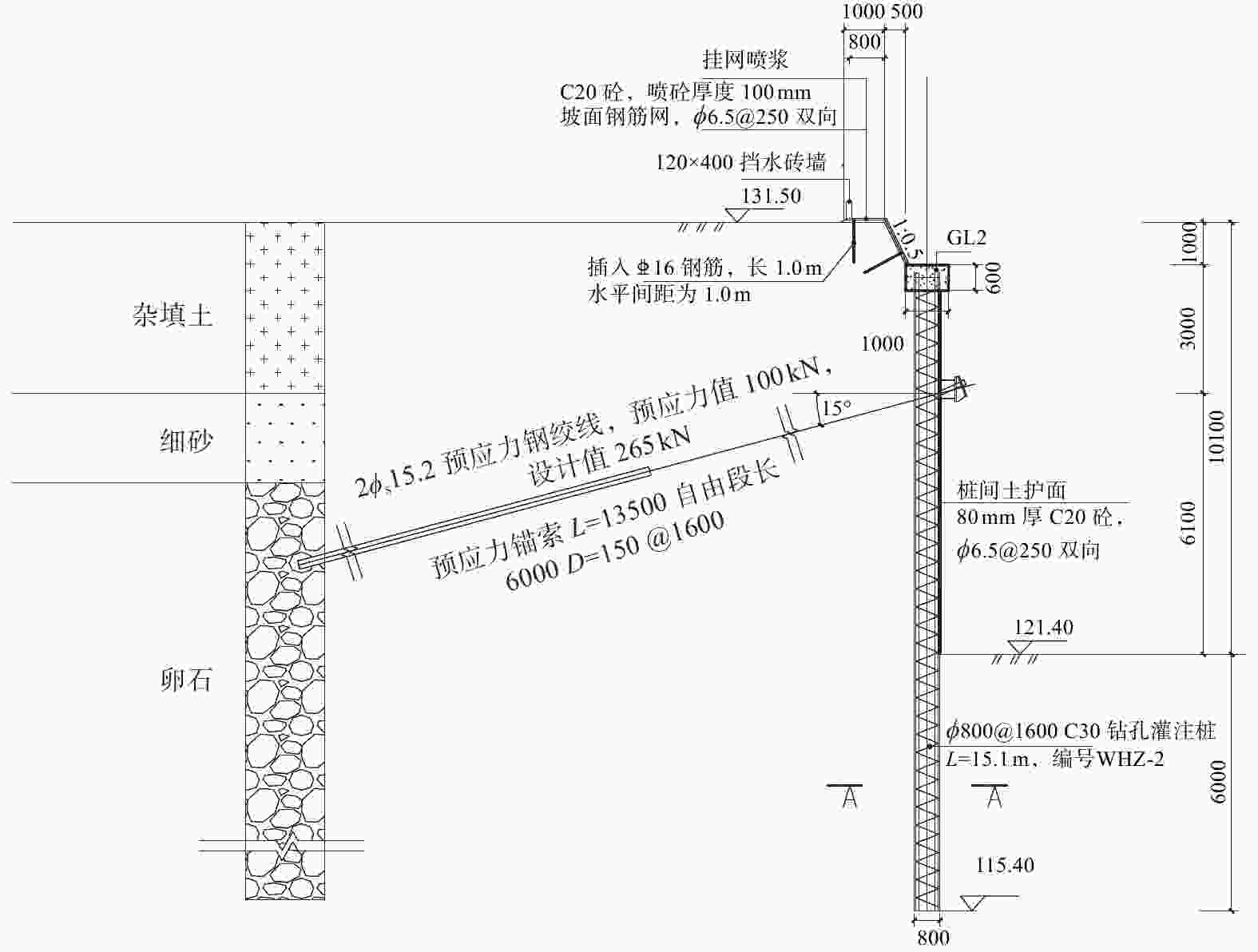
Discussion on Design Method of Single Point Pile-anchor Supporting Structure
-
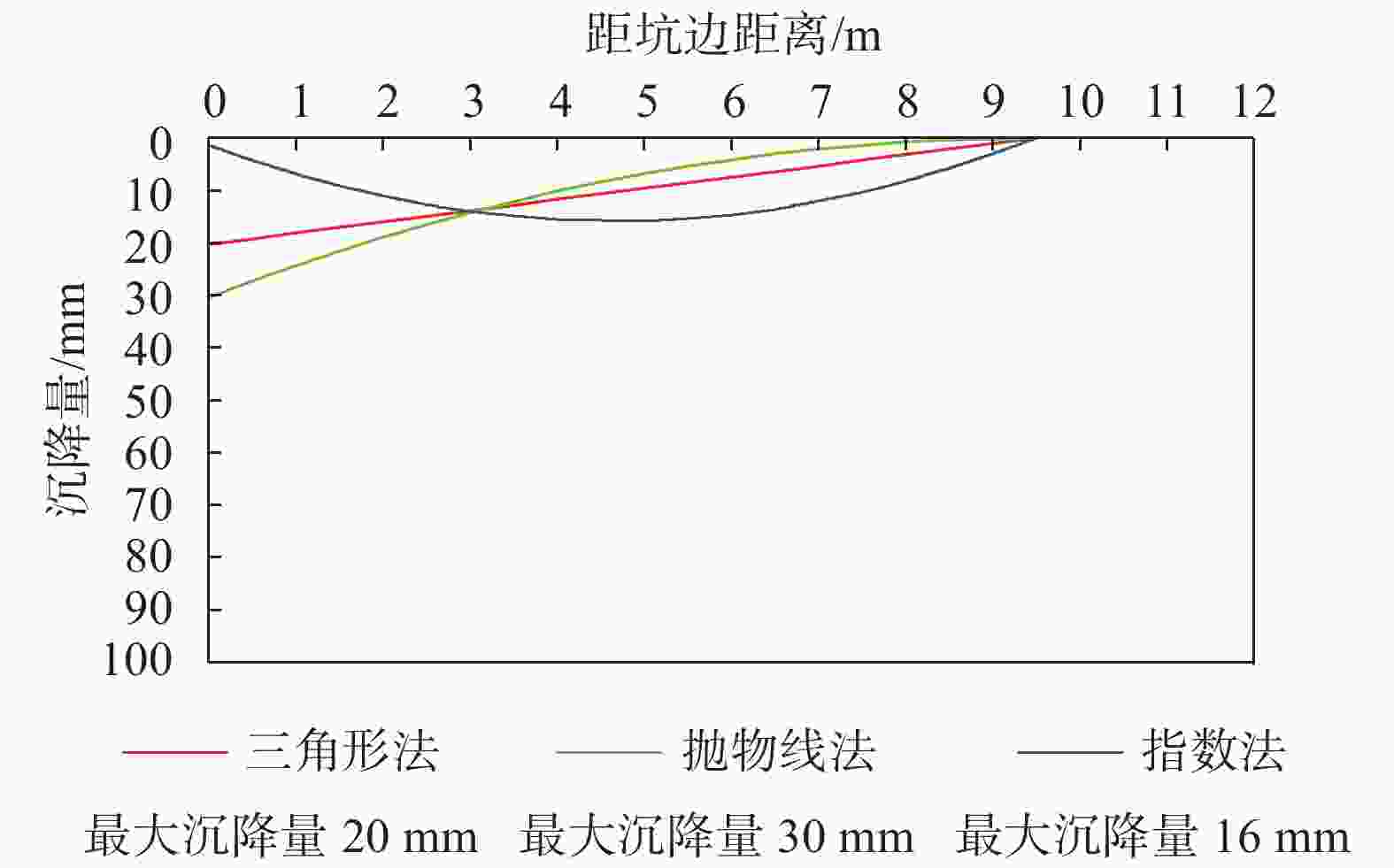
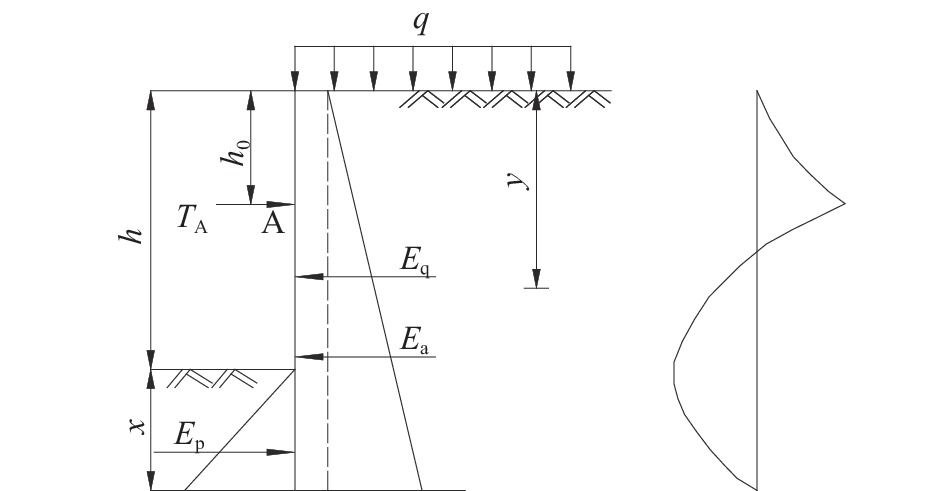
摘要: 为探索合理的深基坑单支点桩锚支护设计方法，兼顾其安全可靠性和经济合理性，以工程实例为分析背景，分别采用静力平衡法、等值梁法、弹性支点法、有限元法对支护桩的内力、位移、嵌固深度、支锚力以及基坑周围地表沉降等进行计算。结果表明：对于支护桩的内力，静力平衡法和等值梁法的计算结果较大，弹性支点法次之，有限元分析法最小；对于支护桩的位移，采用理正深基坑支护设计软件中的弹性法模拟支护桩的变形较差，而采用有限元软件模拟的结果更符合支护桩的实际变形；对于地表沉降量，“理正软件”中的“m”法计算结果更符合实际。Abstract: In order to optimize the design of single-point pile-anchor support for deep foundation pit, both safety reliability and economic rationality should be guaranteed. Based on an engineering example, static equilibrium method, equivalent beam method, elastic fulcrum method and finite element method were used respectively to calculate the internal force, displacement, minimum soil depth, anchorage force and ground settlement around the foundation pit. The results show that: the internal force of supporting pile calculated by static equilibrium method and equivalent beam method is the largest, then elastic fulcrum method, and smallest by finite element method. In the displacement analysis of the supporting pile, the elastic fulcrum method is used to simulate the deformation of the supporting structure, but the finite element method is more in line with the actual deformation of the supporting pile. As for surface settlement, the results calculated by "m" method are basically consistent with the results of finite element analysis.
-
表 1 主要土层物理力学参数
土层 平均层
厚/${\text{m}}$渗透系数
/（m·d-1）重度$\gamma $
/（$ {\rm{kN}} \cdot {{\rm{m}}^{ - 3}} $）黏聚力
c/${\text{kPa}}$内摩擦角
$\varphi $/（°）锚杆锚
固力/${\text{kPa}}$杂填土 4.0 17.5 12 15 30 细砂 2.1 18.5 2 28 50 卵石 15 150 20 2 35 120 
下载: 导出CSV
表 2 内力和位移计算值
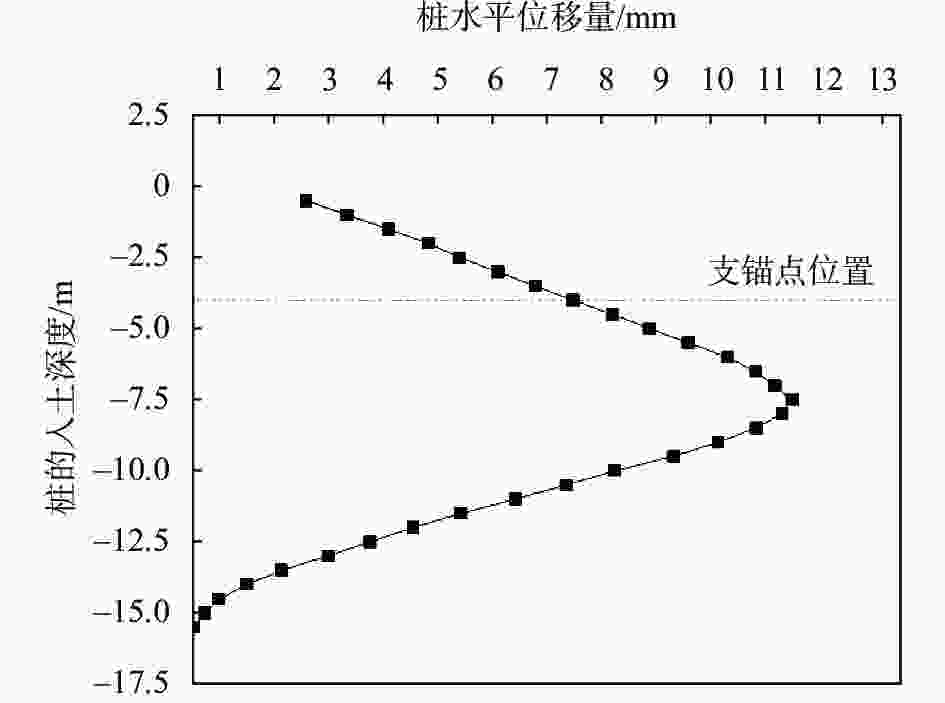
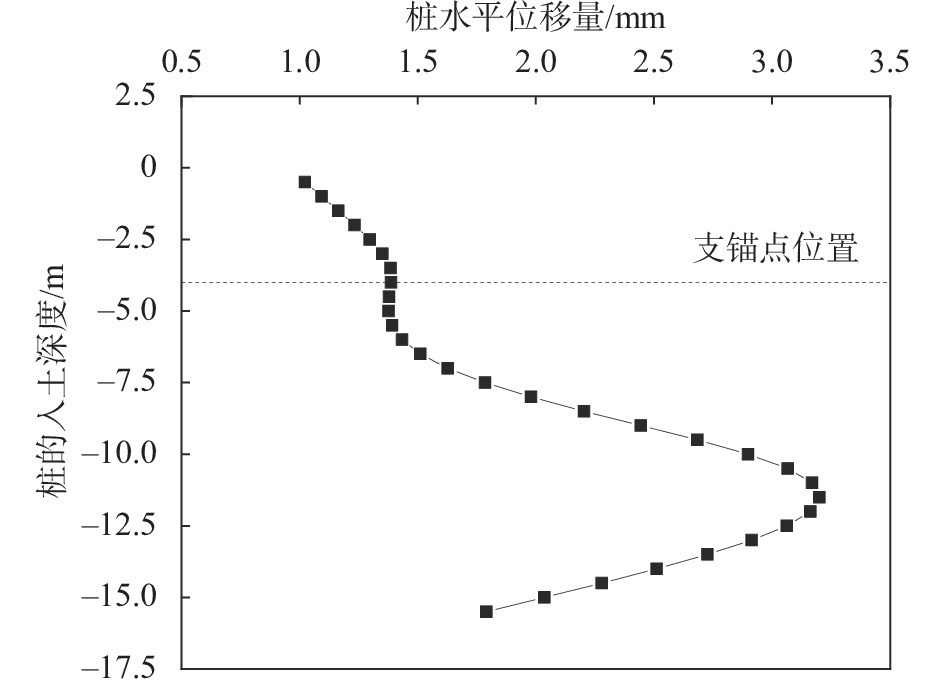
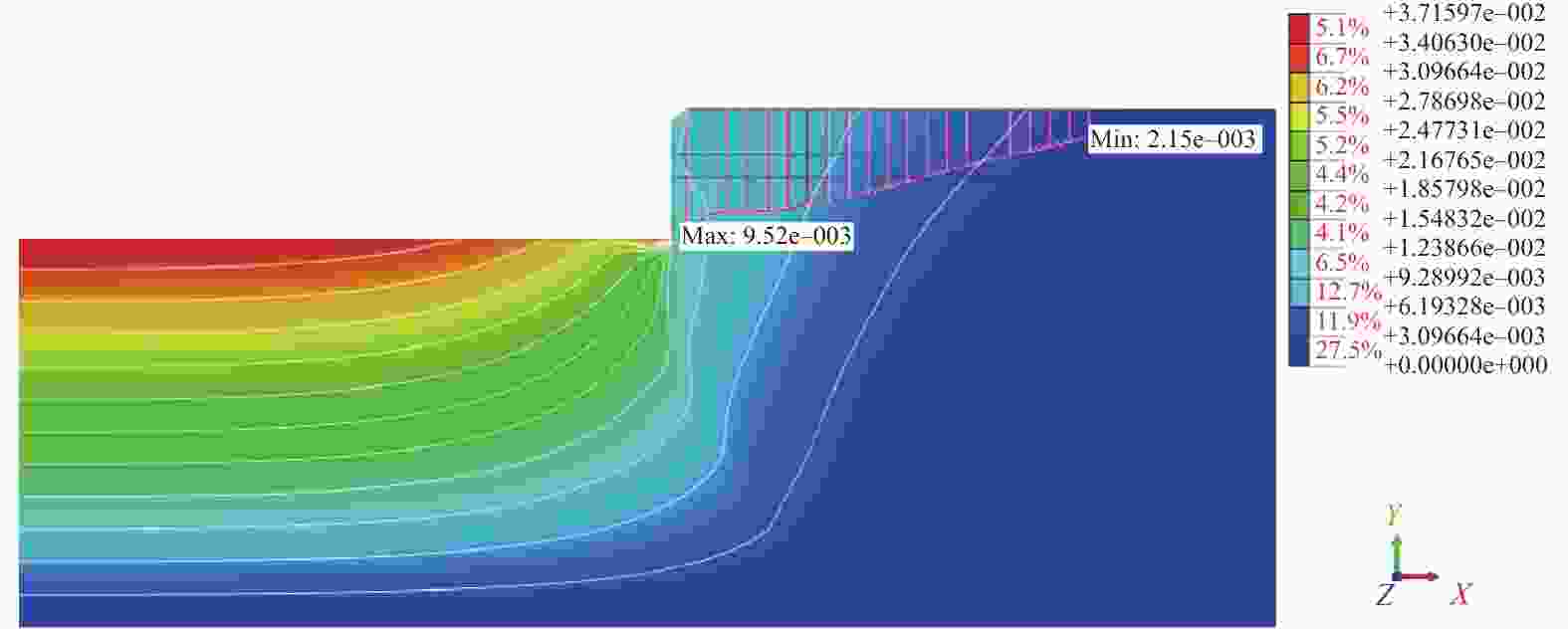
内力计算方法 剪力$\left| {{V_{\max }}} \right|$/kN 弯矩$\left| {{M_{\max }}} \right|$/(kN·m) 位移量$\left| \Delta \right|$/mm 静力平衡法 173.22 470.59 等值梁法 277.70 454.61 弹性支点法 227.55 416.72 11.53 有限元分析法 182.88 282.70 3.18
下载: 导出CSV
表 3 支护桩入土深度和支锚力
内力计算方法 入土深度/m 水平支锚力/kN 静力平衡法 1.94 193 等值梁法 4.39 127.7 理正验算（弹性法） 6 195.14 Midas GTX NX验算 6 80.48
下载: 导出CSV
表 4 单支点桩锚支护结构稳定性
计算方法 整体稳定性 抗隆起稳定性 抗倾覆稳定性 安全系数${K_{\rm{s}}}$ 是否满足${K_{\rm{s}}} > 1.{\text{3} }$ 支护底部逐层验算${K_{\rm{s}}}$ 是否满足${K_{\rm{s}}} > 1.6$ 安全系数${K_{\rm{t}}}$ 是否满足${K_{\rm{t}}} > 1.{\text{2} }$ 等值梁法 满足 12.34 满足 3.2 满足 理正验算（弹性法） 1.538 满足 12.97 满足 1.88 满足
下载: 导出CSV
-
[1] 陈 沙,王贻荪. 复杂土层深基坑挡土桩受力分析[J]. 工程建设与设计,2000,(1):15-17. doi: 10.3969/j.issn.1007-9467.2000.01.006 [2] 赖鹏程. 弹性地基梁“m”法在深基坑支护结构中应用[J]. 中国水运(理论版),2006,(11):61-63. [3] 胡贺松. 深基坑桩锚支护结构稳定性及受力变形特性研究[D]. 长沙: 中南大学, 2009. [4] 朱丽霞. 基于等值梁法的基坑支护设计[J]. 土工基础,2010,24(6):42-45. doi: 10.3969/j.issn.1004-3152.2010.06.013 [5] 陈玖颖. 桩锚支护结构内力计算方法研究及其在基坑工程中的应用[D]. 长沙: 湖南大学, 2012. [6] 郑 毅,施鑫竹. 对弹性支点法的认识[J]. 有色金属设计,2016,43(3):34-37. doi: 10.3969/j.issn.1004-2660.2016.03.009 [7] 张有祥,周宏磊,李云耀. 关于《建筑基坑支护技术规程》支挡结构弹性支点法的讨论[J]. 工业建筑,2017,47(8):111-116,138. [8] 虢 希,李 聪,曾立军,等. 桩锚支护中桩体内力与变形的计算方法探讨[J]. 建筑结构,2019,49(S2):834-840. [9] 梅 岭,方龙建,黄献文,等. 基于地基系数法的桩前土体抗力计算公式推导[J]. 沈阳工业大学学报,2020,42(6):701-705. doi: 10.7688/j.issn.1000-1646.2020.06.15 [10] 胡玉丽. 基于改进增量法的桩锚支护结构位移与内力计算[D]. 兰州: 兰州理工大学, 2020. [11] 刘起霞. 基坑工程[M]. 北京: 中国电力出版社, 2015. [12] 姜晨光. 基坑工程理论与实践[M]. 北京: 化学工业出版社, 2009. [13] 中华人民共和国住房和城乡建设部. JGJ120—2012 建筑基坑支护技术规程[S]. 北京: 中国建筑工业出版社, 2012. [14] LIU Y F, LIU S A. FLAC3D Simulation analysis of excavation and supporting structure of deep foundation pit[J]. International Journal of Earth Sciences and Engineering,2016,9(5):2321-2326. [15] 王歇成, 邵 敏. 有限元基本原理和数值方法[M]. 北京: 清华大学出版社, 2001. -
图(10) / 表(4)
计量
- 文章访问数: 153
- HTML全文浏览量: 34
- PDF下载量: 43
- 被引次数: 0
