测量数据中粗差的探测与处理

陈磊; 姚培军; 孙愿平; 王兰

doi:10.3969/j.issn.1007-2993.2022.04.011

测量数据中粗差的探测与处理

doi: 10.3969/j.issn.1007-2993.2022.04.011

1.
中兵勘察设计研究院有限公司，北京　100053
2.
交通运输部规划研究院，北京　100028

详细信息

作者简介:
陈　磊，男，1984年生，汉族，安徽宿州人，硕士研究生，高级工程师，主要从事工程测量、变形监测等工作。E–mail：1950531417@qq.com

中图分类号: P 258
计量
- 文章访问数: 354
- HTML全文浏览量: 82
- PDF下载量: 47
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-31
- 网络出版日期: 2022-08-08
- 刊出日期: 2022-08-08

Detection and Adjustment of Gross Errors In Survey Data

1.
China Ordnance Industry Survey and Geotechnical Institute Co., Ltd., Beijing 100053, China
2.
Transport Planning and Research Institute Ministry of Transport, Beijing 100028, China

摘要

摘要: 利用巴尔达传统粗差检验方法检验剔除出数据中的粗差，并通过稳健估计方法处理含有粗差的数据以及传统平差方法处理剔除过粗差的数据，与加入粗差前的数据处理结果作对比，比较不同粗差处理方法的优缺点。经比较得出：在保证一定迭代计算次数的条件下，稳健估计能够达到抵抗粗差的目的；巴尔达粗差探测在数据中只含有一个粗差的情况下，与稳健估计相比，在满足一定精度要求的前提下，更能保证计算效率；在数据含有多个粗差的情况下，可利用稳健估计方法进行处理。
- 粗差 /
- 巴尔达 /
- 选权迭代 /
- 探测 /
- 测量数据处理
Abstract: Baarda's traditional gross error test method was used to test and eliminate the gross errors in the data. The data with gross errors were processed by robust estimation method and traditional adjustment method respectively, and the results were compared with those before adding gross errors. The advantages and disadvantages of different gross error processing methods were compared. It is concluded that under the condition of ensuring a certain number of iterative calculations, robust estimation can achieve the purpose of resisting gross errors. Compared with robust estimation, Baarda gross error detection can ensure the calculation efficiency on the premise of meeting certain accuracy requirements when there is only one gross error in the data. When the data contains multiple gross errors, the robust estimation method can be used for processing.
- gross error /
- Baarda /
- selecting weight iteration /
- detection /
- survey data adjustment

HTML全文

图 1 水准网略图

下载: 全尺寸图片幻灯片

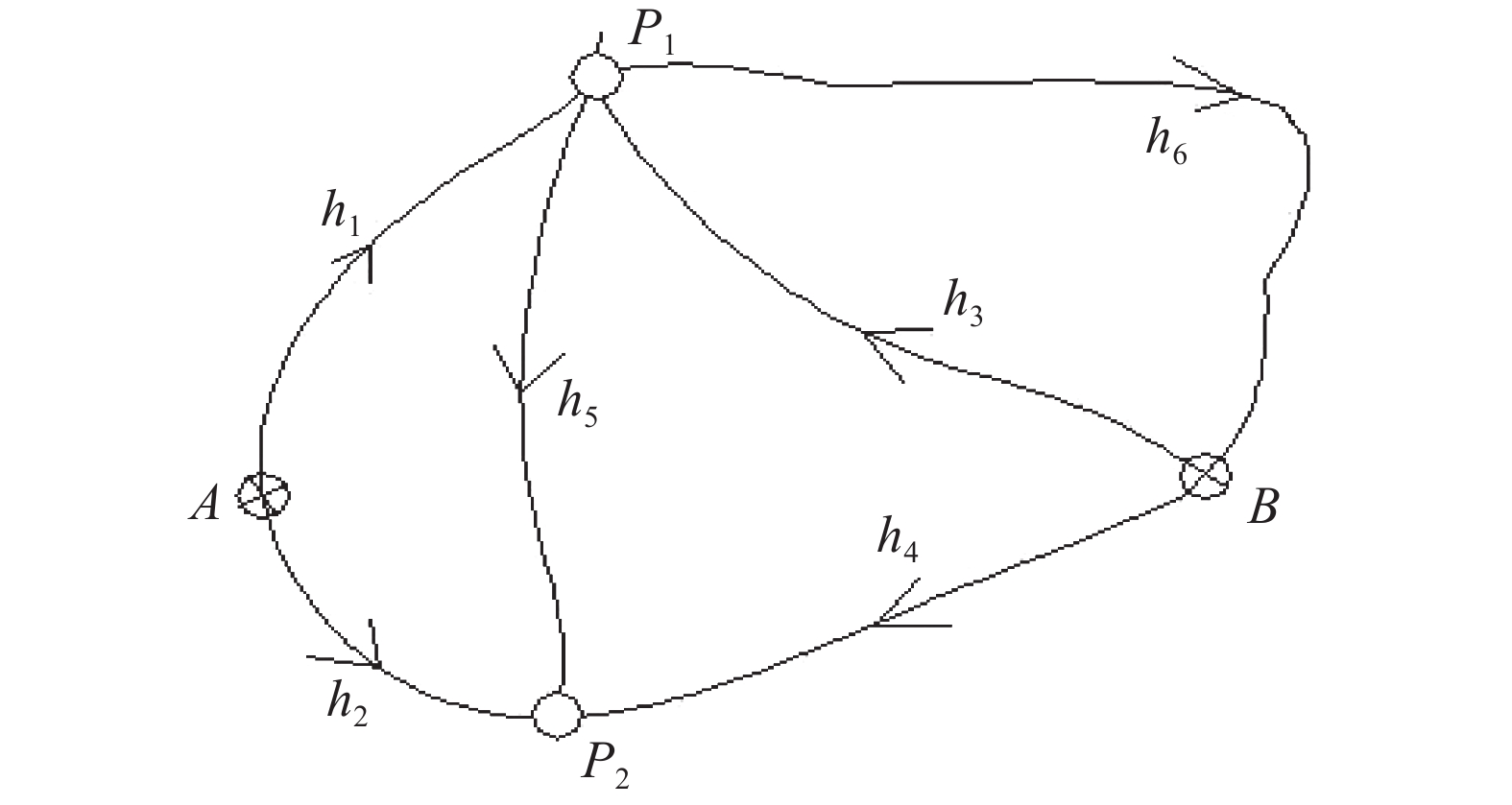
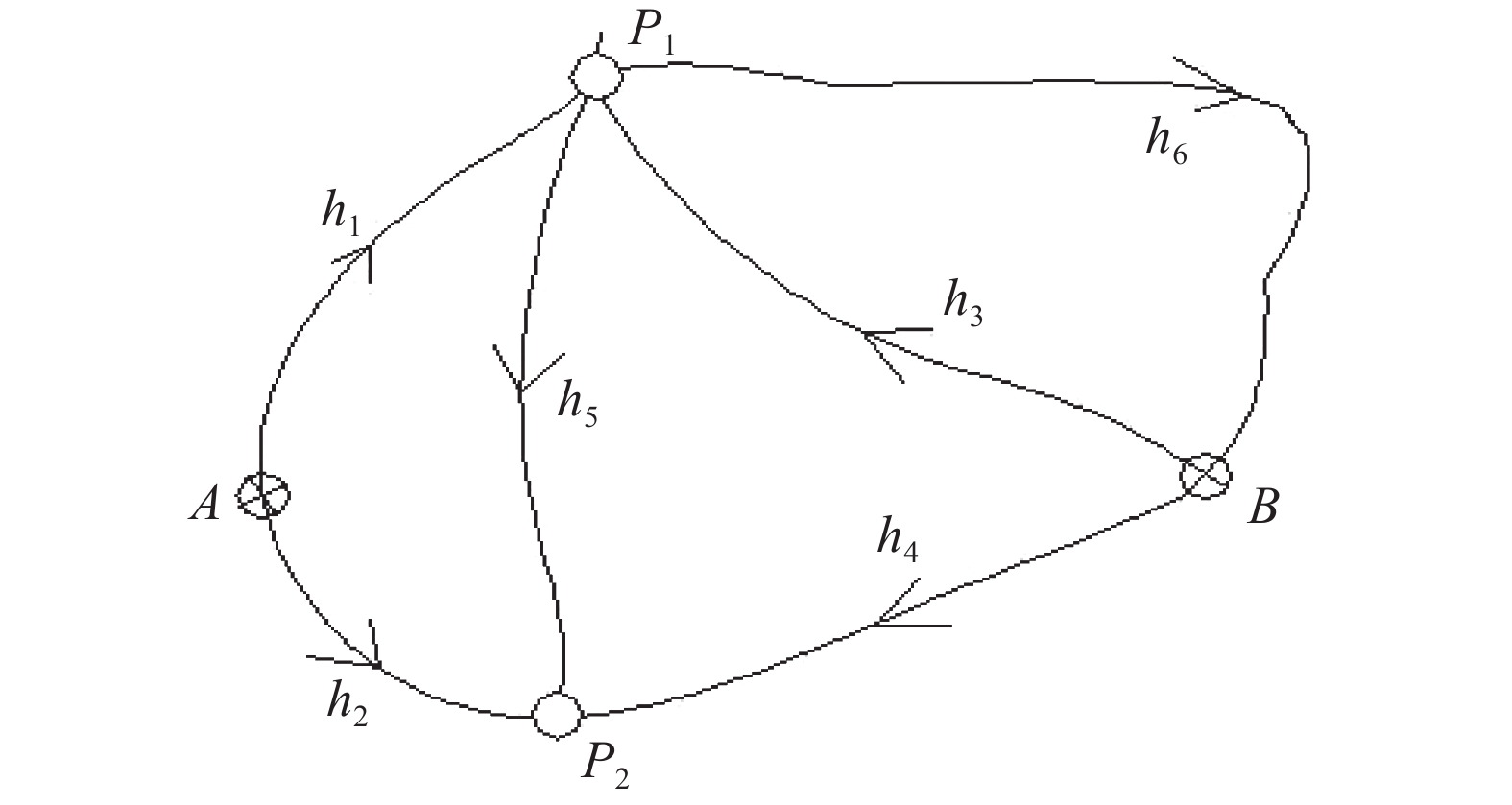
表 1 观测数值

测段编号	观测高差/m	线路长度/km	已知高程/m
h₁	+1.359	1.1	HA=5.016
h₂	+2.209	1.7	HB=6.016
h₃	+0.363	2.3
h4	+1.012	2.7
h₅	+0.657	2.4
h₆	−0.357	4.0

下载: 导出CSV

表 2 正态u结果

测段编号	改正数v/m	改正数方差	改正数中误差	正态u
h₁	0.018822	0.0035	0.059160798	0.318145
h₂	−0.10583	0.0056	0.074833148	−1.41421
h₃	0.014822	0.0108	0.103923048	0.142622
h₄	0.09117	0.0117	0.108166538	0.842871
h₅	0.068349	0.0086	0.092736185	0.737023
h₆	−0.02082	0.0211	0.14525839	−0.14334

下载: 导出CSV

表 3 高程表

点名	高程H/m	备注
A	5.0160	已知点
B	6.0160	已知点
P₁	6.3751
P₂	7.0308

下载: 导出CSV

表 4 高程值

点名	高程H/m	备注
A	5.0160	已知点
B	6.0160	已知点
P₁	6.3743
P₂	7.0277

下载: 导出CSV

表 5 权因子迭代计算(h₁—h₃)

次数	路线
	h₁		h₂		h₃
	w₁	v₁/mm	w₂	v₂/mm	w₃	v₃/mm
1	1	18.8217	1	−105.8296	1	14.82
2	0.053	5.349	0.009	−126.5299	0.067	1.3493
3	0.178	2.9735	0.008	−138.2333	0.741	−1.0265
4	0.336	2.4502	0.007	−149.9846	0.974	−1.5498
5	0.408	1.9086	0.007	−157.9085	0.645	−2.0914
	…	…	…	…	…	…
23	1.00E+10	0	0.005	−192.9972	0.25	−4
24	1.00E+10	0	0.005	−192.9987	0.25	−4
25	1.00E+10	0	0.005	−192.9994	0.25	−4
26	1.00E+10	0	0.005	−192.9997	0.25	−4
27	1.00E+10	0	0.005	−192.9999	0.25	−4

下载: 导出CSV

表 6 权因子迭代计算（h₄—h₆）

次数	路线
	h₄		h₅		h₆
	w₄	v₄/mm	w₅	v₅/mm	w₆	v₆/mm
1	1	91.17	1	68.3487	1	−20.8217
2	0.011	70.4701	0.015	61.1208	0.048	−7.3493
3	0.014	58.7667	0.016	51.7931	0.136	−4.9735
4	0.017	47.0154	0.019	40.5652	0.201	−4.4502
5	0.021	39.0915	0.025	33.1829	0.225	−3.9086
	…	…	…	…	…	…
23	0.25	4.0028	166.7	0.0028	0.5	−2
24	0.25	4.0013	357.1	0.0013	0.5	−2
25	0.25	4.0006	769.2	0.0006	0.5	−2
26	0.25	4.0003	1667	0.0003	0.5	−2
27	0.25	4.0001	3333	0.0001	0.5	−2

下载: 导出CSV

表 7 平差结果

观测值	权因子	改正数v/mm	平差结果L_i/mm
h₁	1.00E+10	0	1359
h₂	0.005	−192.9999	2016.0001
h₃	0.25	−4	359
h₄	0.25	4.0001	1016.0001
h₅	3333	0.0001	657.0001
h₆	0.5	−2	−359

下载: 导出CSV

表 8 平差结果

点号	高程H/m	备注
A	5.0160	已知点
B	6.0160	已知点
P₁	6.375
P₂	7.0320

下载: 导出CSV

表 9 平差结果

点号	高差改正数/m	改正后高差/m	高程中误差/m	平差后高程/m	备注
A			0.0000	5.0160	已知点
P₁	−0.0007	1.3583	0.0015	6.3743
A			0.0000	5.0160	已知点
P₂	0.0027	2.0117	0.0018	7.0277
B			0.0000	6.0160	已知点
P₁	−0.0047	0.3583	0.0015	6.3743
B			0.0000	6.0160	已知点
P₂	−0.0003	1.0117	0.0018	7.0277
P1			0.0015	6.3743
P₂	−0.0036	0.6534	0.0018	7.0277
P₁			0.0015	6.3743
B	−0.0013	−0.3583	0.0000	6.0160	已知点

下载: 导出CSV

表 10 平差结果

点号	高差改正数/m	改正后高差/m	高程中误差/m	平差后高程/m	备注
A			0.0000	5.0160	已知点
P₁	0.0001	1.3591	0.0014	6.3751
B			0.0000	6.0160	已知点
P₁	−0.0039	0.3591	0.0014	6.3751
B			0.0000	6.0160	已知点
P₂	0.0028	1.0148	0.0024	7.0308
P₁			0.0014	6.3751
P₂	−0.0013	0.6557	0.0024	7.0308
P₁			0.0014	6.3751
B	−0.0021	−0.3591	0.0000	6.0160	已知点

下载: 导出CSV

表 11 平差结果

点号	高差改正数/m	改正后高差/m	高程中误差/m	平差后高程/m	备注
A			0.0000	5.0160	已知点
P₁	0.0000	1.3590	0.0000	6.3750
A			0.0000	5.0160	已知点
P₂	0.0000	2.0160	0.0000	7.0320
B			0.0000	6.0160	已知点
P₁	0.0000	0.3590	0.0000	6.3750
B			0.0000	6.0160	已知点
P₂	0.0000	1.0160	0.0000	7.0320
P₁			0.0000	6.3750
P₂	0.0000	0.6570	0.0000	7.0320
P₁			0.0000	6.3750
B	0.0000	−0.3590	0.0000	6.0160	已知点

下载: 导出CSV

表 12 比较平差结果

点号	平差后高程/m
点号	方法一	方法二	方法三
P₁	6.3743	6.3751	6.3750
P₂	7.0277	7.0308	7.0320

下载: 导出CSV

参考文献(16)

[1]	王仁谦. 一种多个粗差的定位与估值的方法[J]. 华侨大学学报, 2004, 25(2): 153-155.
[2]	佘光辉,刘恩斌. 非线性模型抗差最小二乘估计及其应用[J]. 南京林业大学学报,2005,29(3):9-13.
[3]	李德仁. 利用选择权迭代法进行粗差定位[J]. 武汉测绘学院学报,1984,(1):47-68.
[4]	周江文. 经典误差理论与抗差估计[J]. 测绘学报,1989,18(2):116-120.
[5]	杨元喜. 大地测量相关观测抗差估计理论[J]. 测绘学报,2002,31(2):96-99.
[6]	杨元喜. 卫星精密轨道综合自适应抗差滤波技术[J]. 中国科学(D辑),2003,33(11):1113-1119.
[7]	朱建军. 一种稳健性准则及相应的稳健估计[J]. 测绘工程,1996,5(4):23-27.
[8]	朱建军. 一种可靠的小波去噪质量评价指标[J]. 武汉大学学报(信息科学版),2015,40(2):210-212.
[9]	朱建军. 附不等式约束平差的一种简单迭代算法[J]. 测绘学报,2011,40(2):210-212.
[10]	孙海燕. P-范分布及其抽样分布[J]. 应用概率统计,2003,19(4):425-428.
[11]	孙海燕. 一元P-范分布的参数估计[J]. 武汉大学学报(信息科学版),2003,28(5):552-554.
[12]	王新洲. 方差分量估计的快速算法[J]. 武测科技,1994,(2):18-22.
[13]	王新洲, 陶本藻. 高等测量平差[M]. 北京: 测绘出版社, 2006.
[14]	归庆明. 双k型岭估计及其在GPS快速定位中的应用[J]. 测绘科学技术学报,2006,23(1):9-10.
[15]	欧吉坤. 一种检测粗差的新方法—拟准检定法[J]. 科学通报,1999,44(16):99-103.
[16]	彭军还. L₁范估计的巴尔达型检验及其可靠性[J]. 测绘学报,2005,34(3):208-212. doi: 10.3321/j.issn:1001-1595.2005.03.004