Influence of Double Track Shield Tunnel Overpassing Construction on Existing Subways Based on HSS Model
-
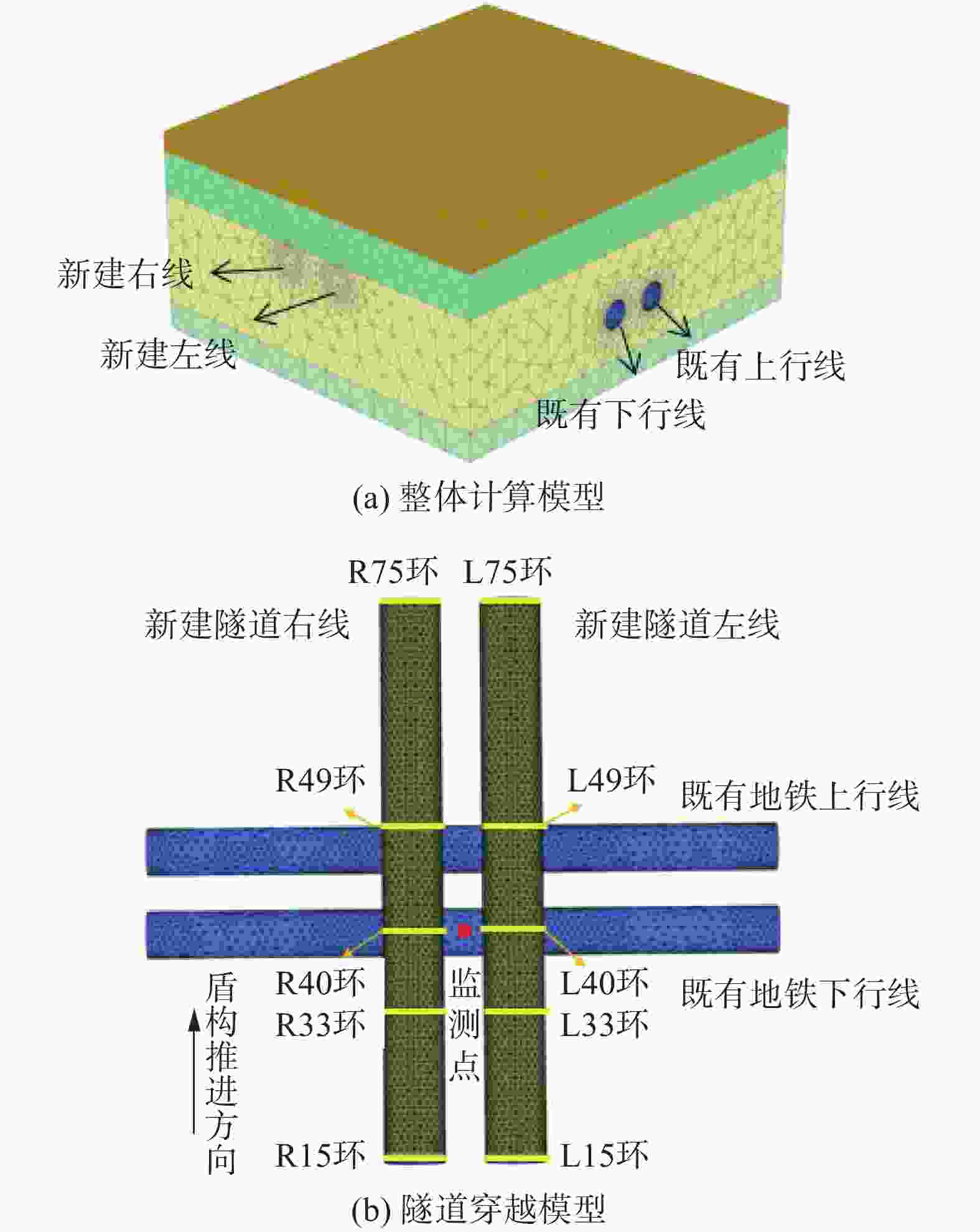
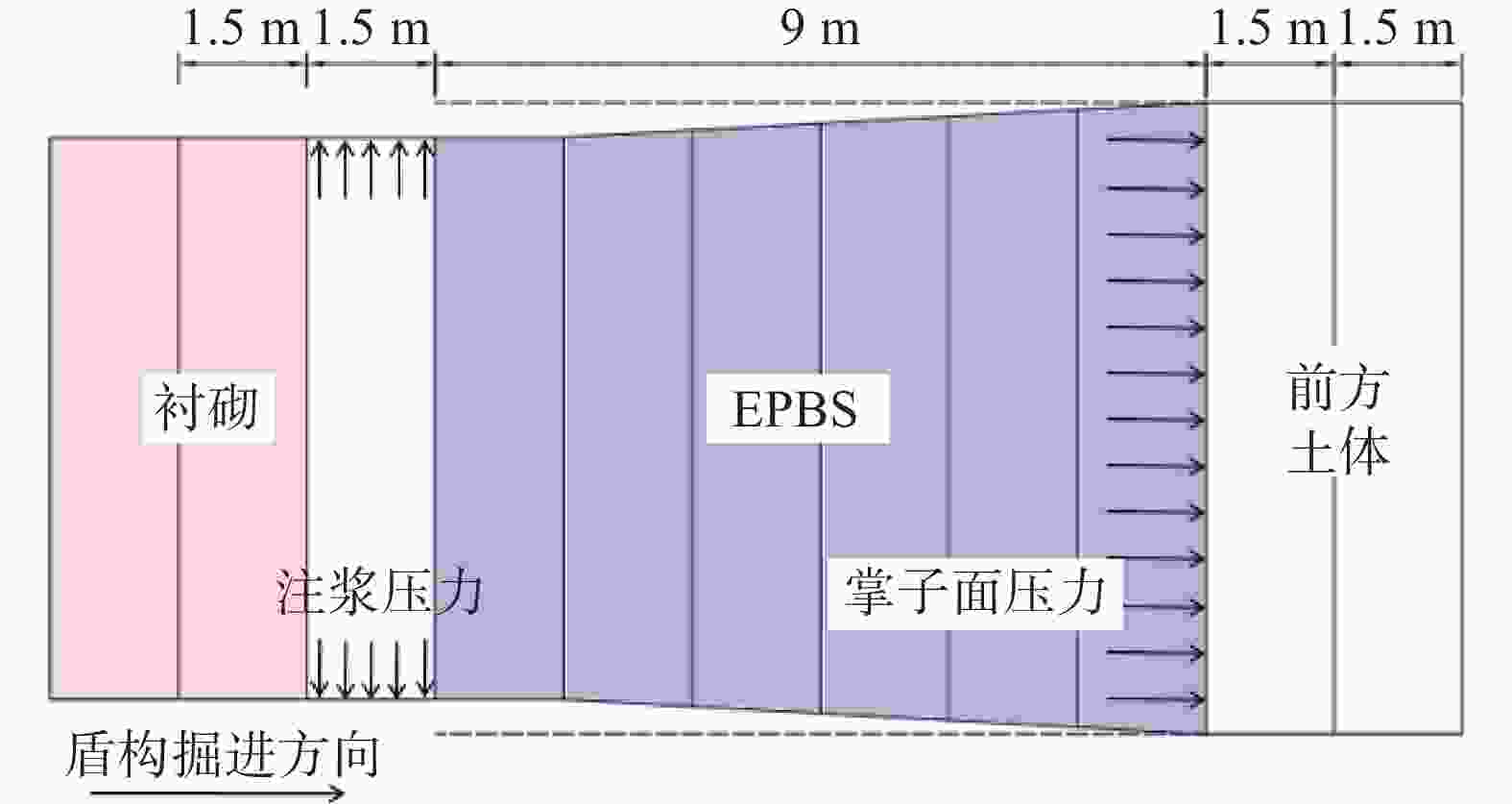
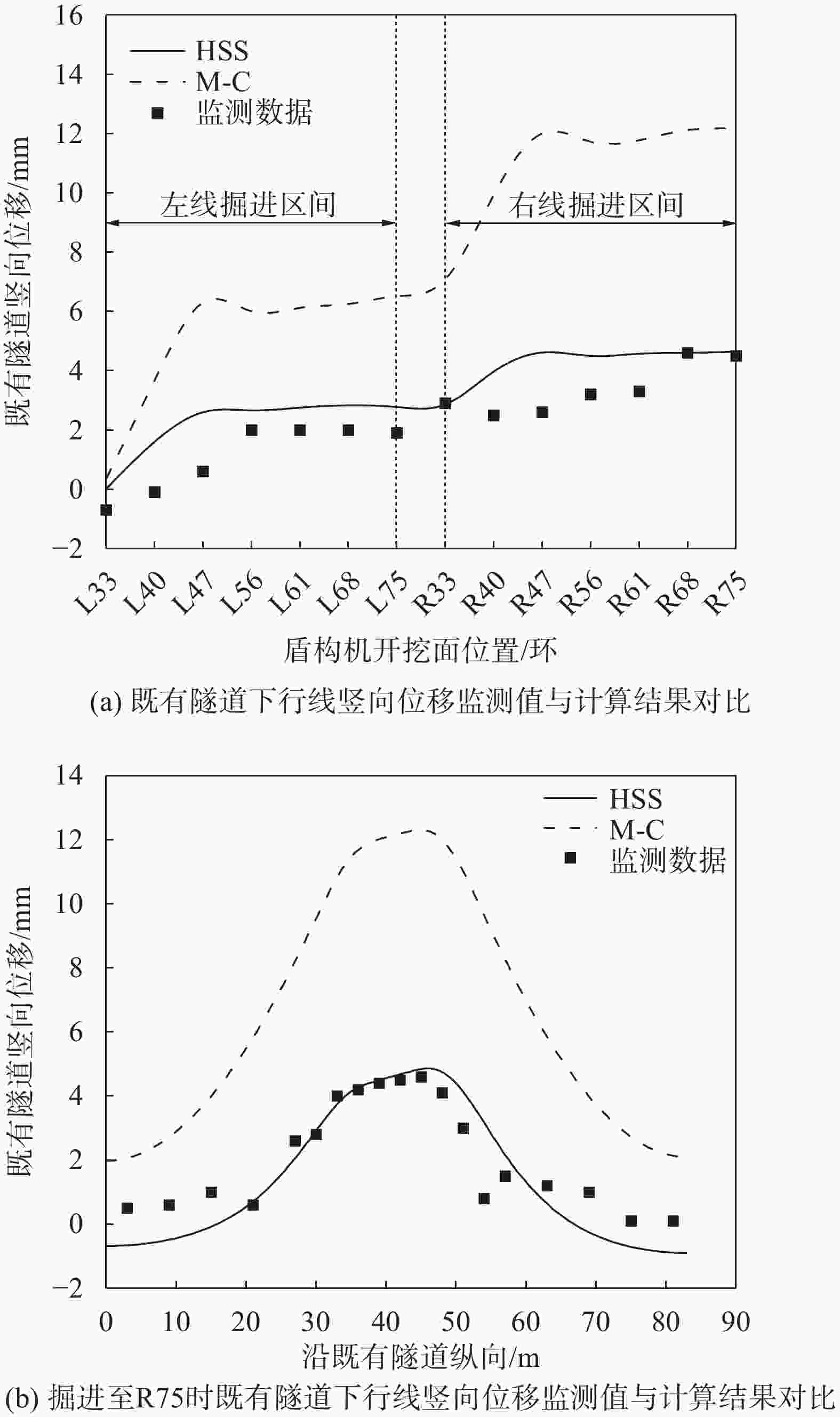
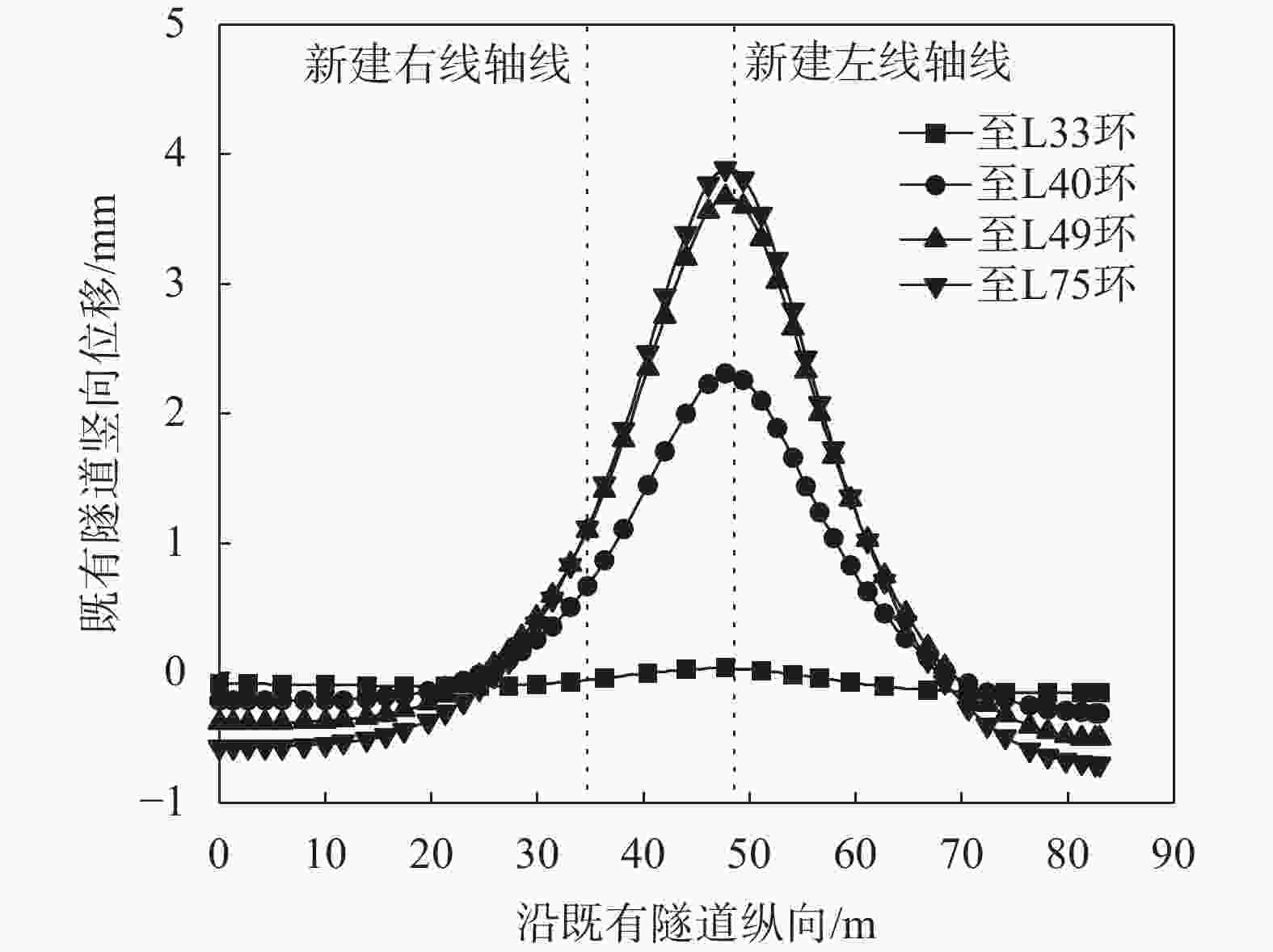
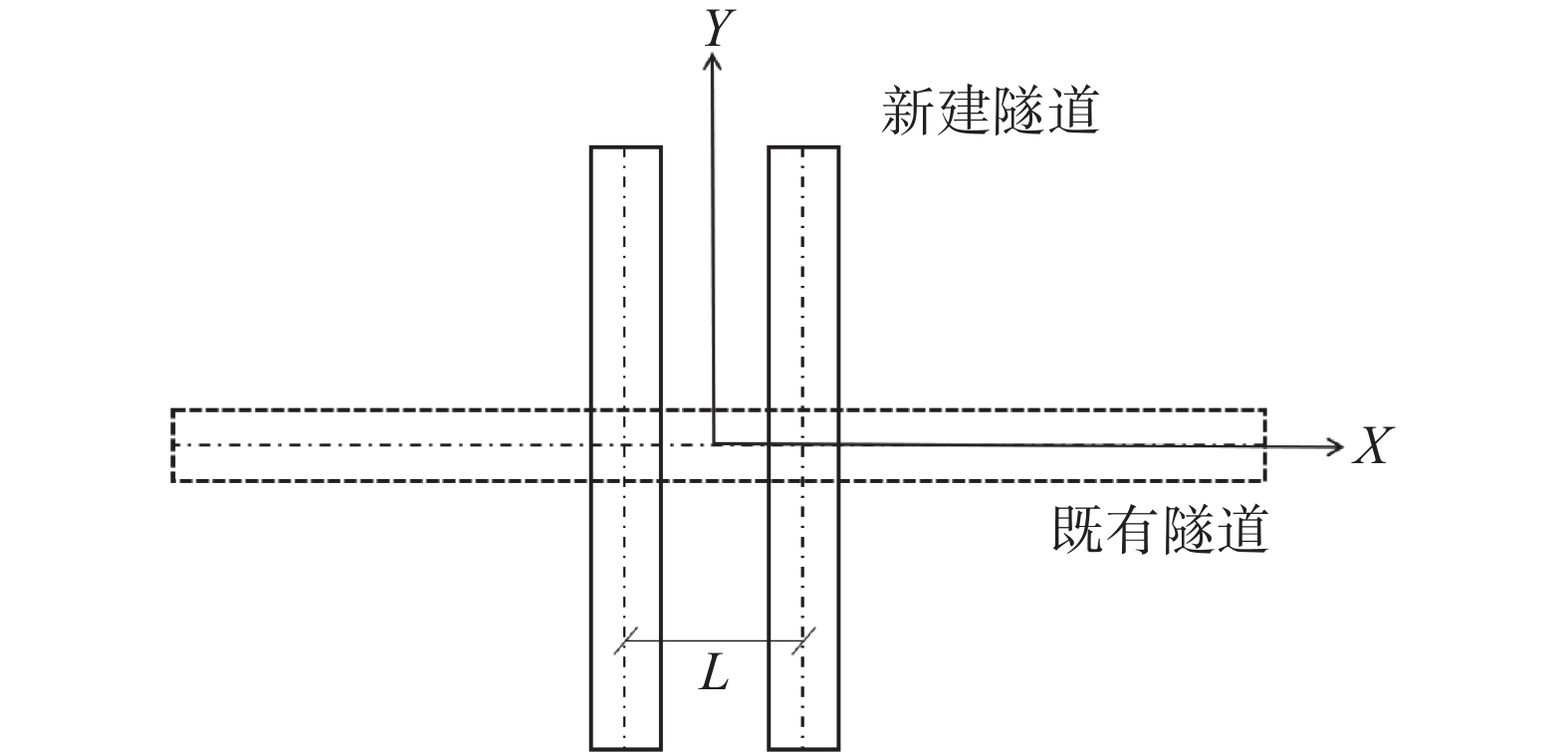
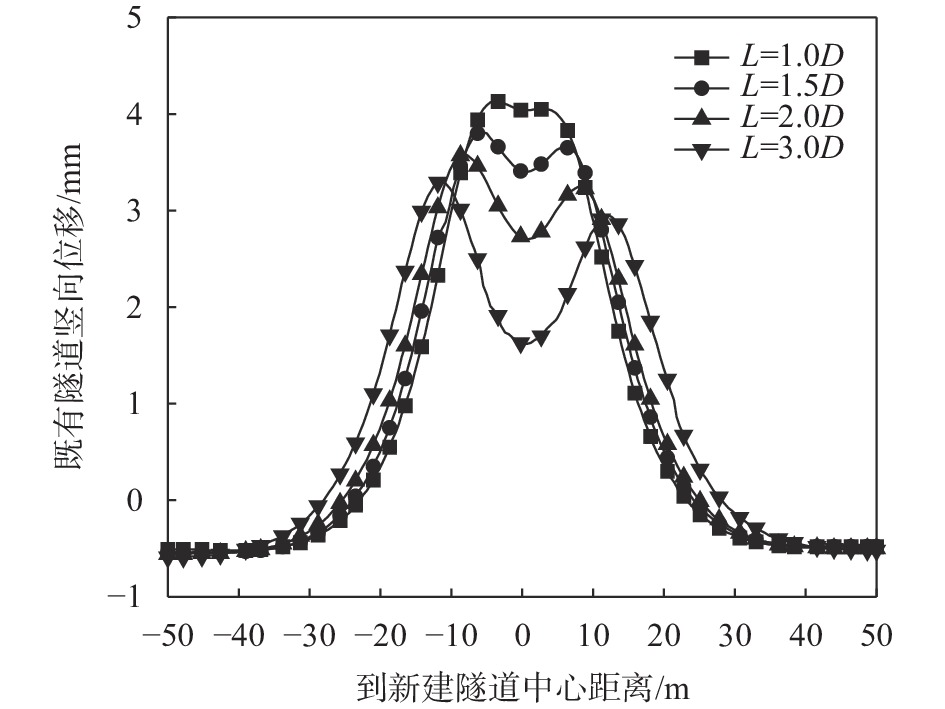
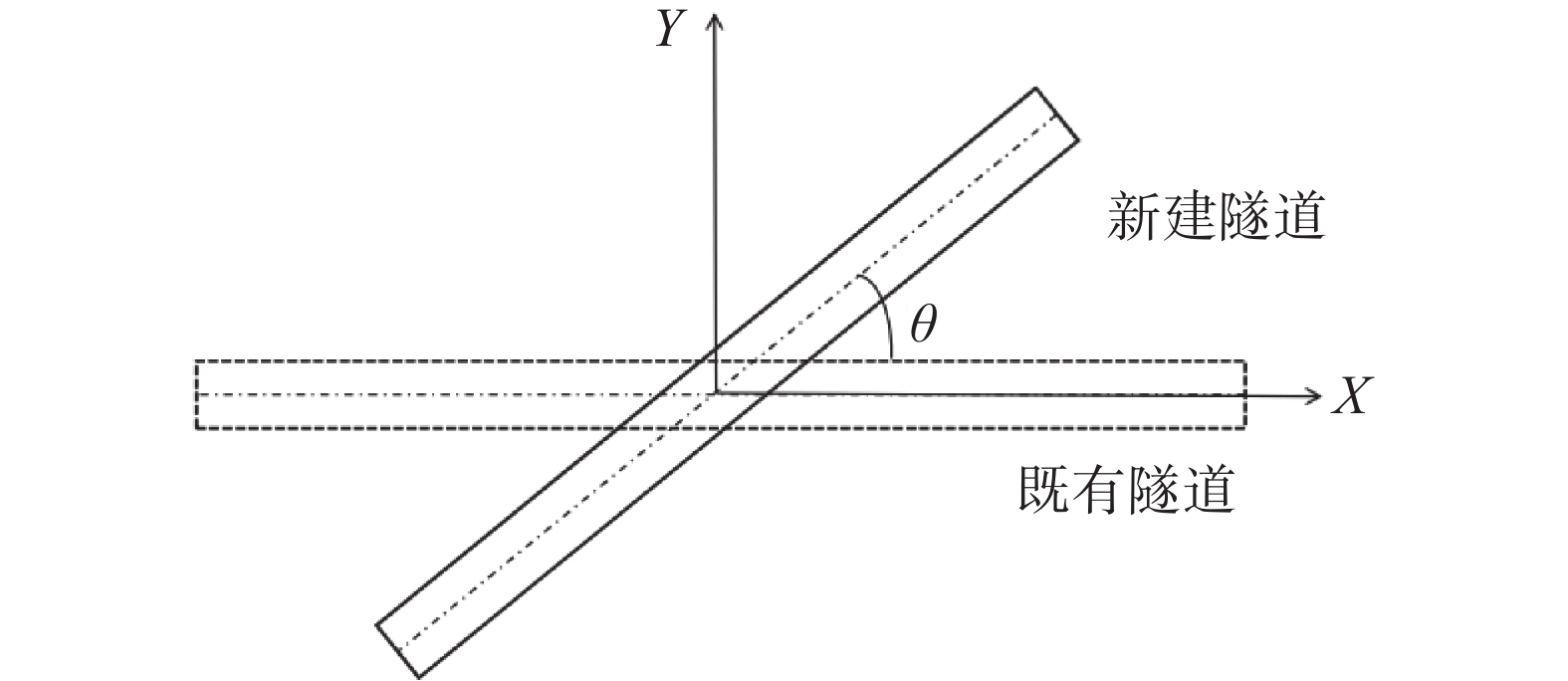
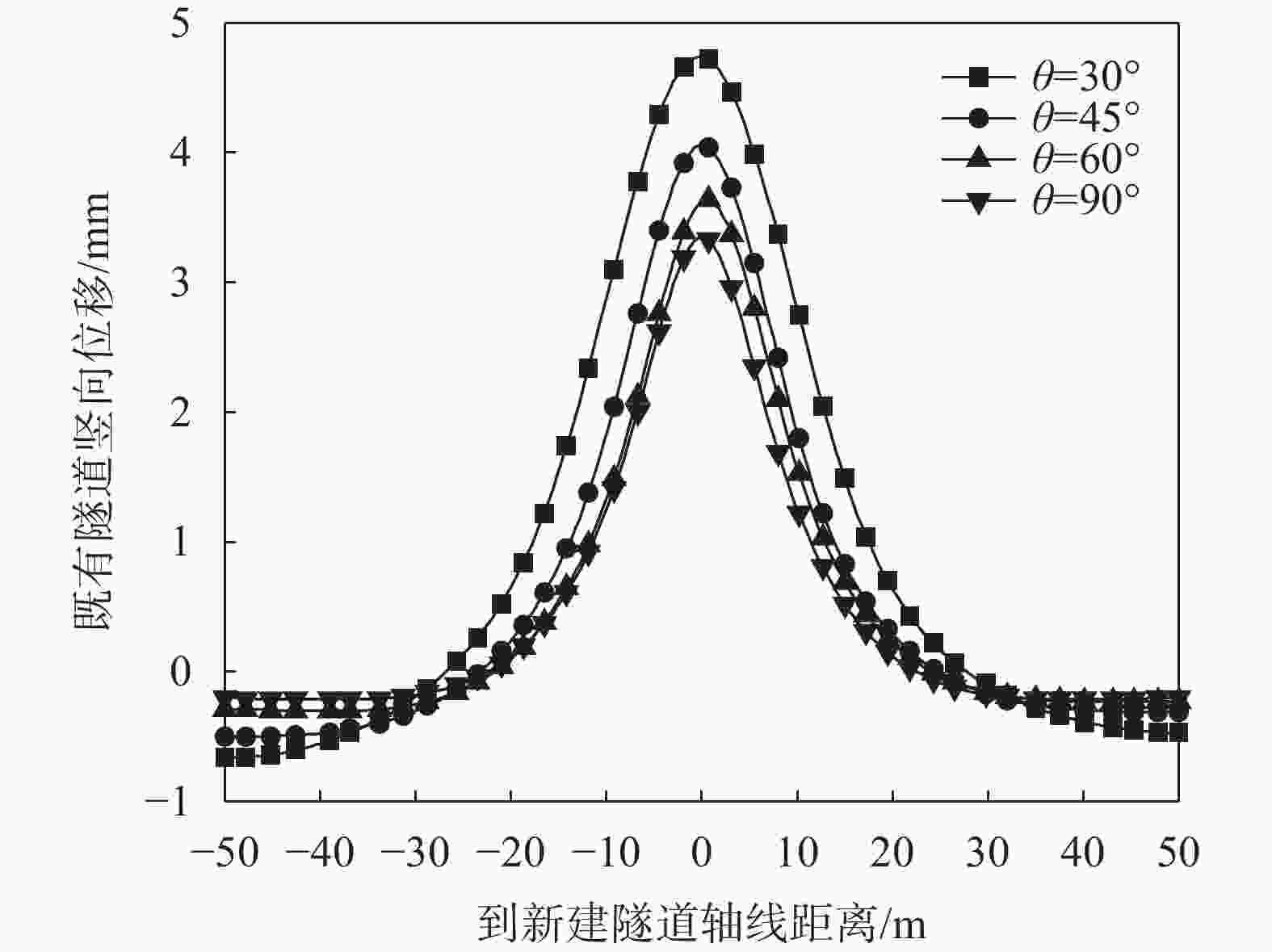
摘要: 针对某新建盾构隧道近接上跨既有地铁项目,基于小应变硬化模型(HSS),建立了三维有限元模型,通过与实测数据和莫尔–库伦模型计算结果的对比,验证了HSS模型计算的可靠性和优越性。在此基础上,进一步分析了新建隧道施工引起的既有隧道竖向变形特征,及隧道水平净距和叠交角度两参数对既有隧道变形的影响规律。结果表明:HSS模型计算结果与实测值吻合较好,能有效预测既有地铁隧道的变形;在新建隧道上跨穿越的影响下,既有地铁隧道产生竖向隆起变形,且变形主要发生在盾构下穿前的1.5倍新建隧道直径到穿越后的2倍新建隧道直径范围内;既有地铁隧道隆起峰值点会随着盾构二次穿越而发生偏移,且其竖向变形曲线呈现出“双峰”趋势;增大双线隧道水平净距和新旧隧道叠交角度,都能使既有隧道的变形减小。Abstract: A three-dimensional finite element model was established based on the HSS constitutive model for a newly constructed shield tunnel adjacent to an existing subway project. The correctness of the numerical calculation was verified by comparing it with measured data. On this basis, further analysis was conducted on the vertical deformation characteristics of existing tunnels caused by the construction of new tunnels, as well as the influence of the two parameters of tunnel horizontal clearance and overlap angle on the deformation of existing tunnels. The results show that the calculated results of HSS model are in good agreement with the measured values, and can effectively predict the deformation of existing subway tunnel. Under the influence of the new tunnel overpassing, the existing subway tunnel has vertical uplift deformation, and the deformation mainly occurs in the range of 1.5 times the diameter of the new tunnel before the shield tunneling under-crossing to 2 times the diameter of the new tunnel after the crossing. The uplift peak point of the existing subway tunnel will shift with the second crossing of the shield, and its vertical deformation curve shows a "double peak" trend. Increasing the horizontal clearance of double track tunnels and the overlapping angle of new and old tunnels can reduce the deformation of existing tunnels.
-
表 1 土层及结构参数
名称 γ/(kN·m−3) c'/(kN·m−2) φ'/(°) $E_{50}^{{\text{ref}}}$/(kN·m−2) $E_{{\text{oed}}}^{{\text{ref}}}$/(kN·m−2) $E_{{\text{ur}}}^{{\text{ref}}}$/(kN·m−2) E'/(kN·m−2) ν $G_0^{{\text{ref}}}$/(kN·m−2) $ \gamma_{_{0.7}} $ 碎石填土 19.0 0 15 3500 3500 14000 3500 21000 2×10−4 砂质粉土 19.2 4 24 7000 7000 28000 14000 42000 2×10−4 淤泥质粉质黏土 17.3 13.5 10.5 2500 2500 10000 12500 15000 1.5×10−4 粉质黏土 19.4 25 14 6000 6000 24000 30000 36000 1.5×10−4 衬砌 24 2.93×108 0.1 盾壳 120 2×108 0 表 2 土层参数
名称 γ/(kN·m−3) c'/(kN·m−2) φ'/(°) $E_{50}^{{\text{ref}}}$/(kN·m−2) $E_{{\text{oed}}}^{{\text{ref}}}$f/(kN·m−2) $E_{{\text{ur}}}^{{\text{ref}}}$/(kN·m−2) $G_0^{{\text{ref}}}$/(kN·m−2) ${\gamma _{0.7}}$ 淤泥质粉质黏土 18 13.5 10.5 3000 3000 12000 18000 1.5×10−4 -
[1] 于 群. 盾构隧道近距离下穿既有隧道影响规律的研究[D]. 北京: 北京交通大学, 2020. [2] 张盛红. 盾构隧道下穿施工对上部既有隧道的影响研究[D]. 广州: 华南理工大学, 2020. [3] 赵宇鹏. 盾构隧道近距离上跨既有隧道施工影响与控制研究[D]. 合肥: 合肥工业大学, 2020. [4] 陈湘生, 李兴高. 复杂环境下盾构下穿运营隧道综合技术[M]. 北京: 中国铁道出版社, 2011. [5] 房 明, 刘 镇, 周翠英, 等. 新建隧道盾构下穿施工对既有隧道影响的三维数值模拟[J]. 铁道科学与工程学报,2011,8(1):67-72. doi: 10.3969/j.issn.1672-7029.2011.01.013 [6] WANG Y, KONG L W, WANG Y L, et al. Analysis of influence of shield tunneling on overlying underground pipelines based on HSS model[C]//IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2018, 423(1): 012017. [7] 丁 智, 吴云双, 张 霄, 等. 软土盾构隧道近距离穿越既有地铁影响数值分析[J]. 中南大学学报(自然科学版),2018,49(3):663-671. [8] 黄德中, 马险峰, 王俊淞, 等. 软土地区盾构上穿越既有隧道的离心模拟研究[J]. 岩土工程学报,2012,34(3):520-527. [9] LIANG R, XIA T, HONG Y, et al. Effects of above-crossing tunnelling on the existing shield tunnels[J]. Tunnelling and Underground Space Technology,2016,58:159-176. doi: 10.1016/j.tust.2016.05.002 [10] 张琼方, 夏唐代, 丁 智, 等. 盾构近距离下穿对已建地铁隧道的位移影响及施工控制[J]. 岩土力学,2016,37(12):3561-3568. [11] 张孟喜, 张 靖, 吴应明, 等. 全风化岩层中双线盾构上穿近邻地铁隧道影响分析[J]. 土木工程学报,2019,52(9):100-108. [12] 张毫毫, 雷明锋, 刘凌晖, 等. 新建隧道下穿施工对既有上卧盾构隧道扰动影响规律研究[J]. 铁道科学与工程学报,2020,17(2):396-404. [13] 许有俊, 秦浩斌, 李文博, 等. 浅埋暗挖隧道近距离平行上跨对既有盾构隧道的变形影响分析[J]. 现代隧道技术,2022,59(3):118-127. [14] 梁发云, 贾亚杰, 丁钰津, 等. 上海地区软土HSS模型参数的试验研究[J]. 岩土工程学报,2017,39(2):269-278. doi: 10.11779/CJGE201702010 [15] 苏晓堃. 隧道开挖数值模拟的围岩边界取值范围研究[J]. 铁道工程学报,2012,29(3):64-68. doi: 10.3969/j.issn.1006-2106.2012.03.014 [16] BENZ T. Small-strain stiffness of soils and its numerical consequences[M]. Stuttgart: University of Stuttgart, 2007. [17] BRINKGREVE R B J, BROERE W. Plaxis material models manual[M]. Netherlands: [s. n. ], 2006. [18] 王卫东, 王浩然, 徐中华. 上海地区基坑开挖数值分析中土体HS-Small模型参数的研究[J]. 岩土力学,2013,34(6):1766-1774. [19] 吴昌胜, 朱志铎. 不同直径盾构隧道地层损失率的对比研究[J]. 岩土工程学报,2018,40(12):2257-2265. doi: 10.11779/CJGE201812013 [20] 魏 纲. 盾构隧道施工引起的土体损失率取值及分布研究[J]. 岩土工程学报,2010,32(9):1354-1361. [21] 朱才辉, 李 宁. 隧道施工诱发地表沉降估算方法及其规律分析[J]. 岩土力学,2016,37(S2):533-542. -
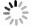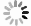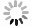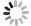




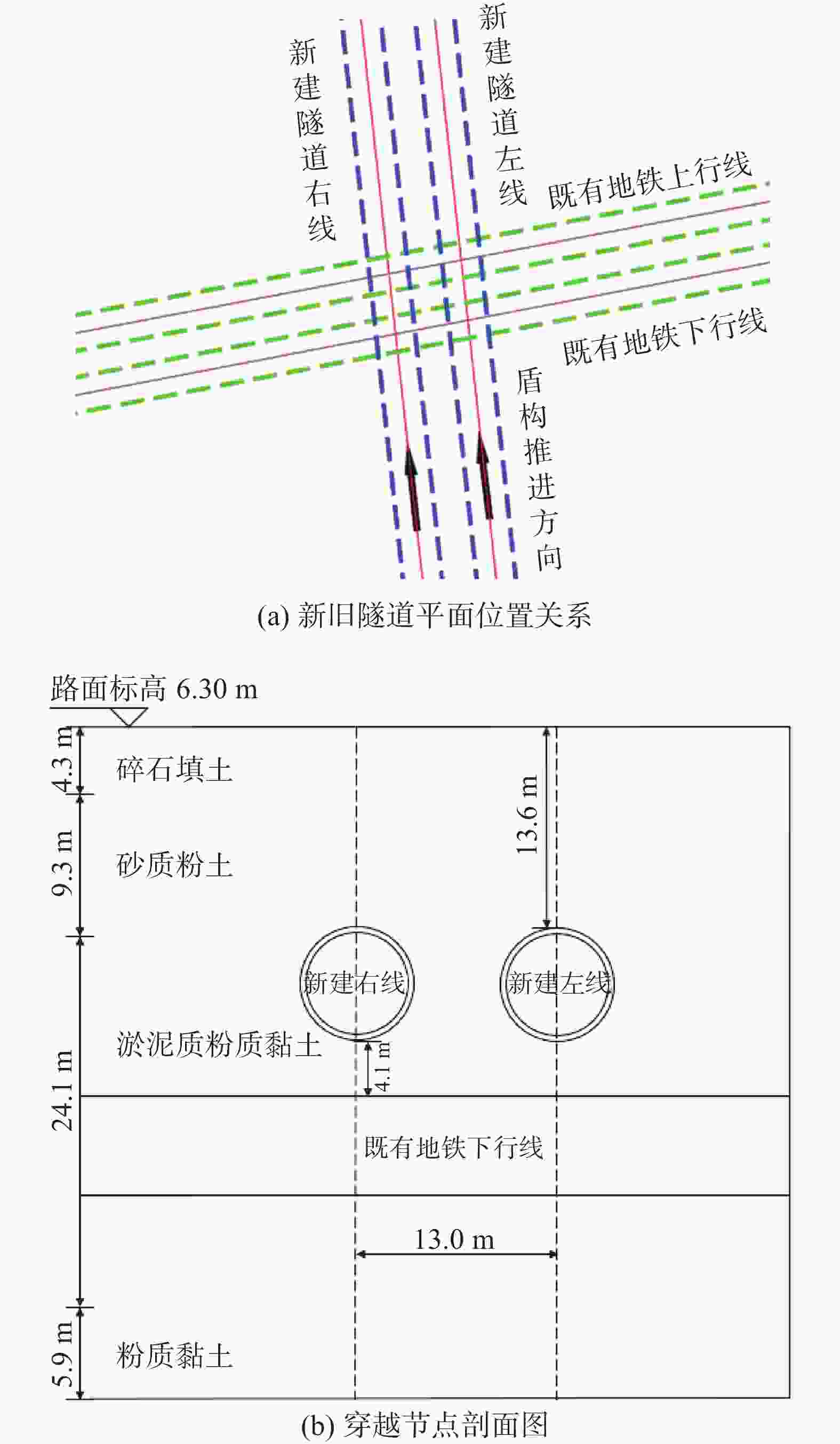
 下载:
下载: