Disturbance Mechanism of Pipe-Jacking Construction on Surrounding Environment
-
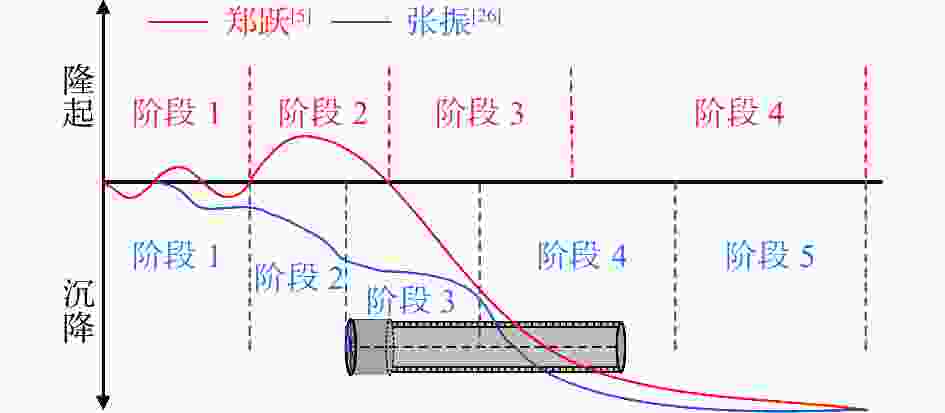
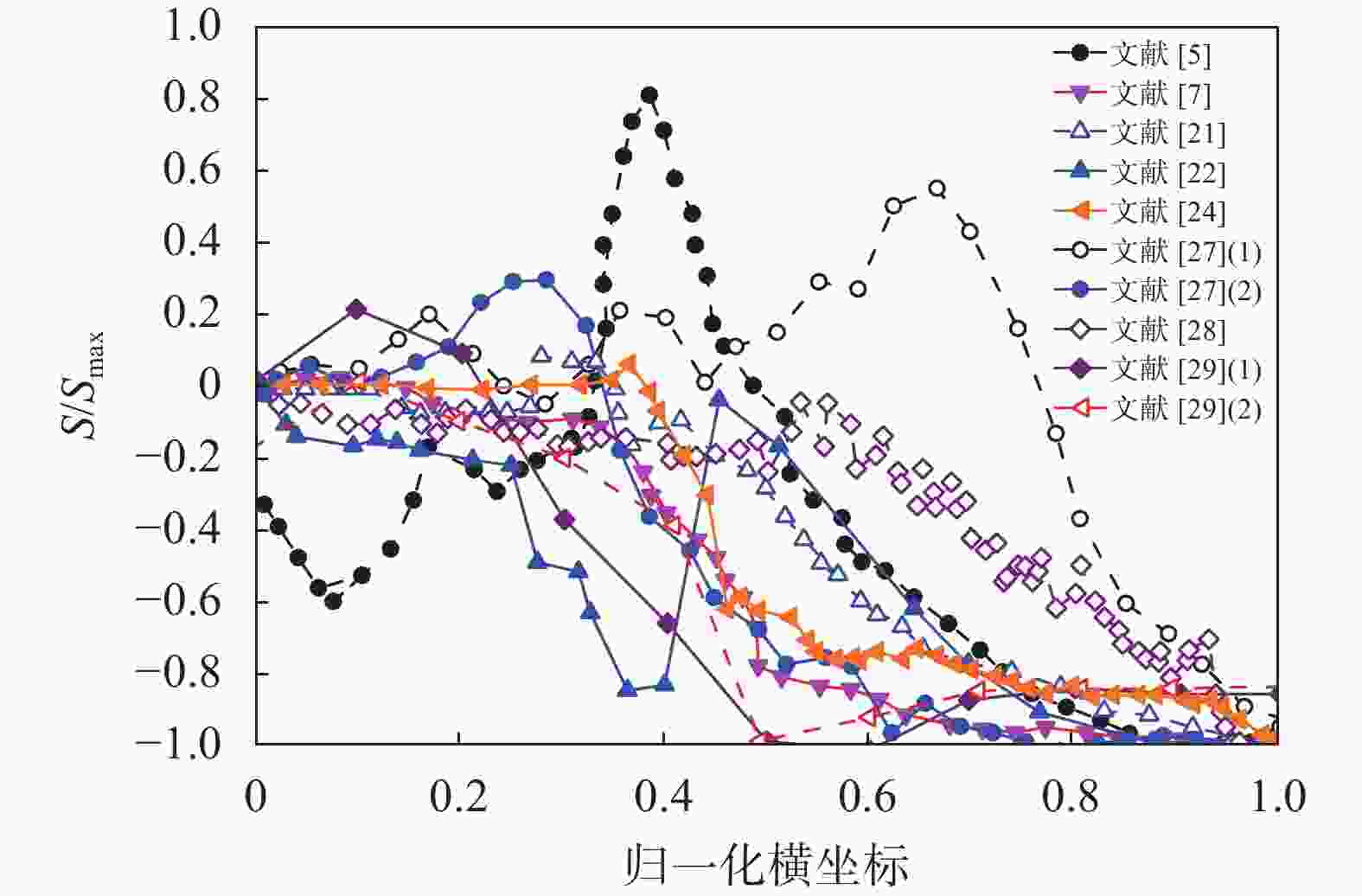
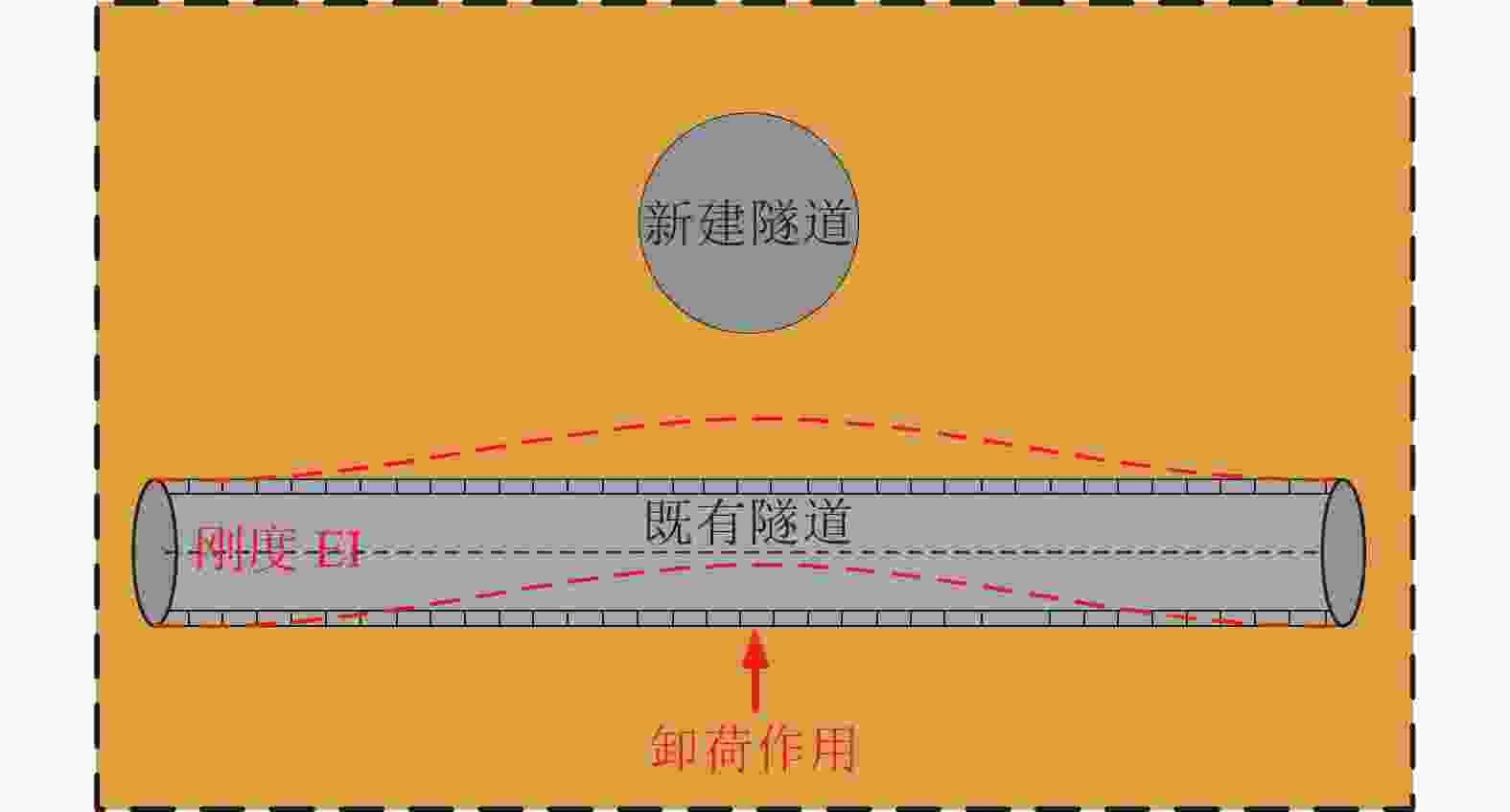
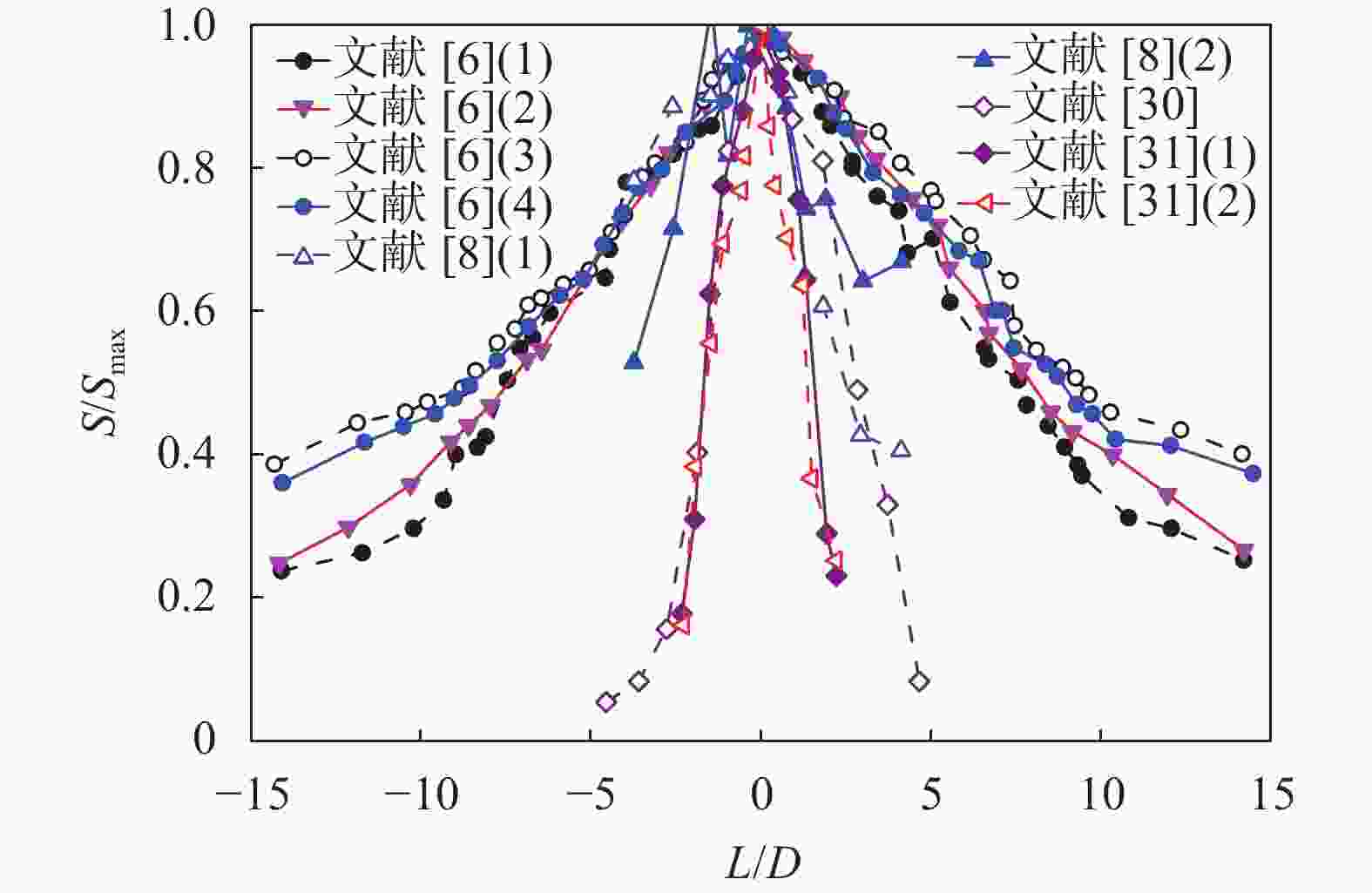
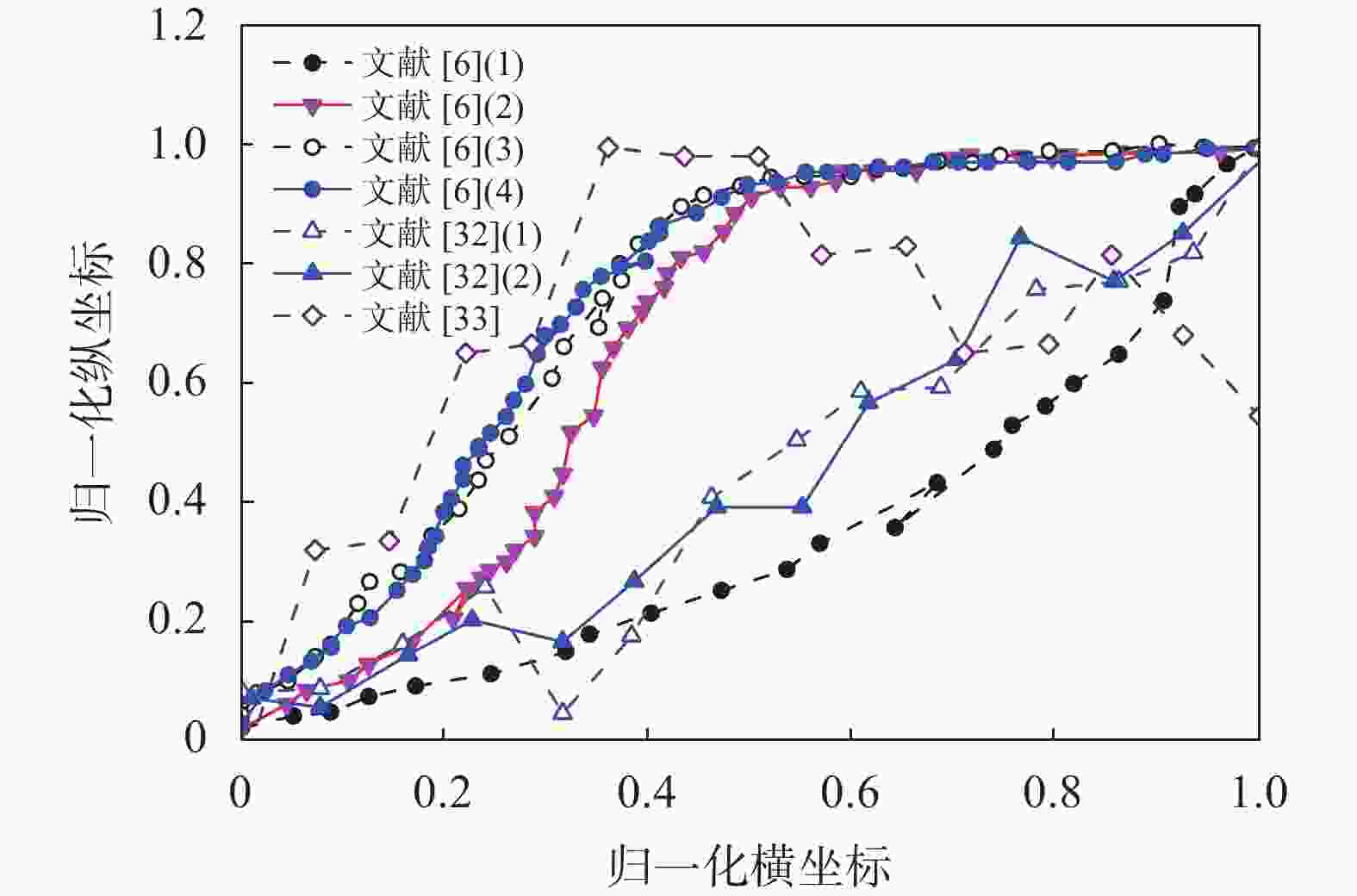
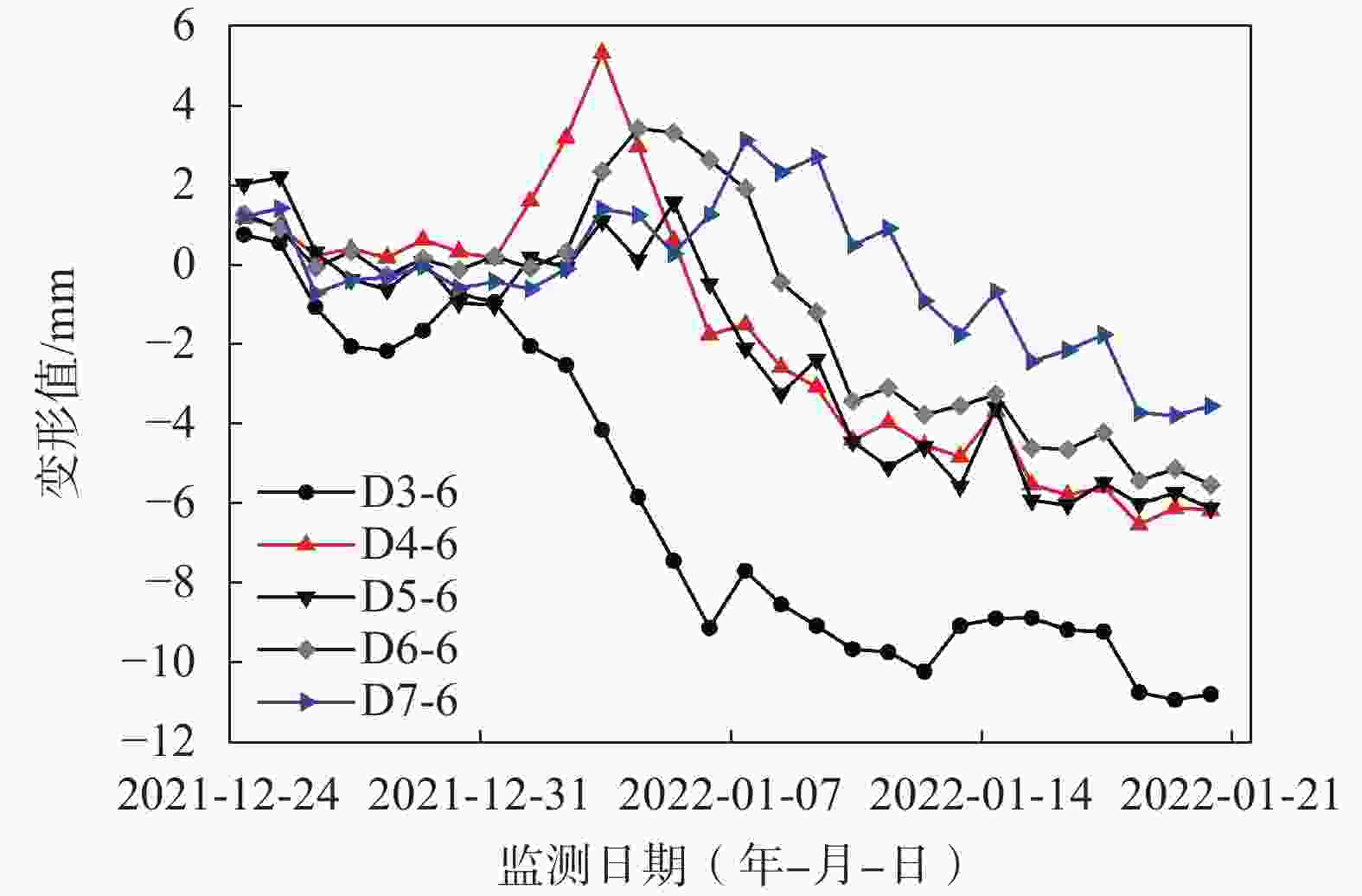
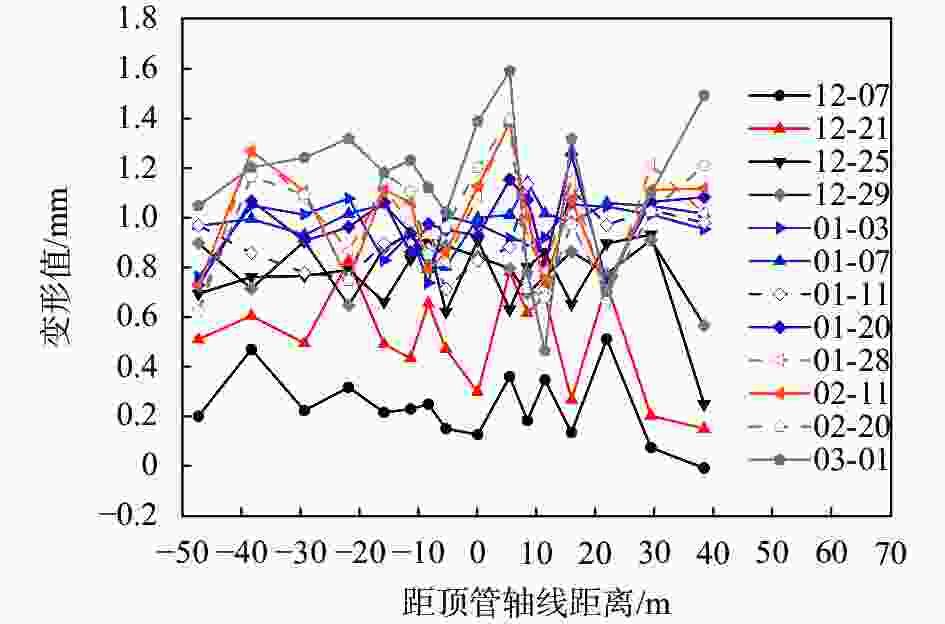
摘要: 为确定顶管施工对周边环境的影响,通过收集工程数据并结合案例监测结果,对顶管施工引起的地表和既有隧道变形机理及规律进行了研究。结论表明:(1)地表断面沉降规律符合Peck公式,影响范围约为1.4~2.6倍顶管直径,地表变形发展曲线分为“先隆起后沉降”和“全程沉降”两种形式;(2)既有隧道上浮总体呈现“反向”Peck曲线,上浮量受既有隧道刚度和所受扰动大小影响,随着时间的增加上浮量先快速增加后趋于稳定;(3)对上穿既有隧道顶管工程进行监测和分析,地表和隧道变形规律与已有研究规律基本一致,采取了数种措施以控制地表和既有隧道的变形,地表最大沉降量约11 mm,既有隧道最大上浮量约1.6 mm。研究成果可为相关顶管设计和施工提供一定参考。Abstract: To determine the impact of pipe-jacking construction on the surrounding environment, engineering data was collected and combined with case monitoring results to study the mechanism and laws of surface and existing tunnel deformation caused by pipe-jacking construction. The conclusions are as follows: (1) The settlement law of the surface section conforms to the Peck formula, with an influence range of about 1.4~2.6 times the diameter of the top pipe. The surface deformation development curve is divided into two forms: "uplift first and then settlement" and "full settlement". (2) The overall uplift of existing tunnels presents a "reverse" Peck curve, and the uplift amount was affected by the stiffness of the existing tunnel and the magnitude of the disturbance it is subjected to. With the increase of time, the uplift amount first increases rapidly and then tends to stabilize. (3) Monitoring and analysis were conducted on the pipe-jacking project of the existing tunnel, and the deformation patterns of the surface and tunnel were basically consistent with existing research patterns. Several measures were taken to control the deformation of the surface and existing tunnel, with a maximum settlement of about 11 mm on the surface and a maximum uplift of about 1.6 mm on the existing tunnel. The research results can provide certain references for the design and construction of related pipe-jacking.
-
Key words:
- pipe-jacking /
- surface deformation /
- existing tunnel /
- disturbance mechanism /
- control measures
-
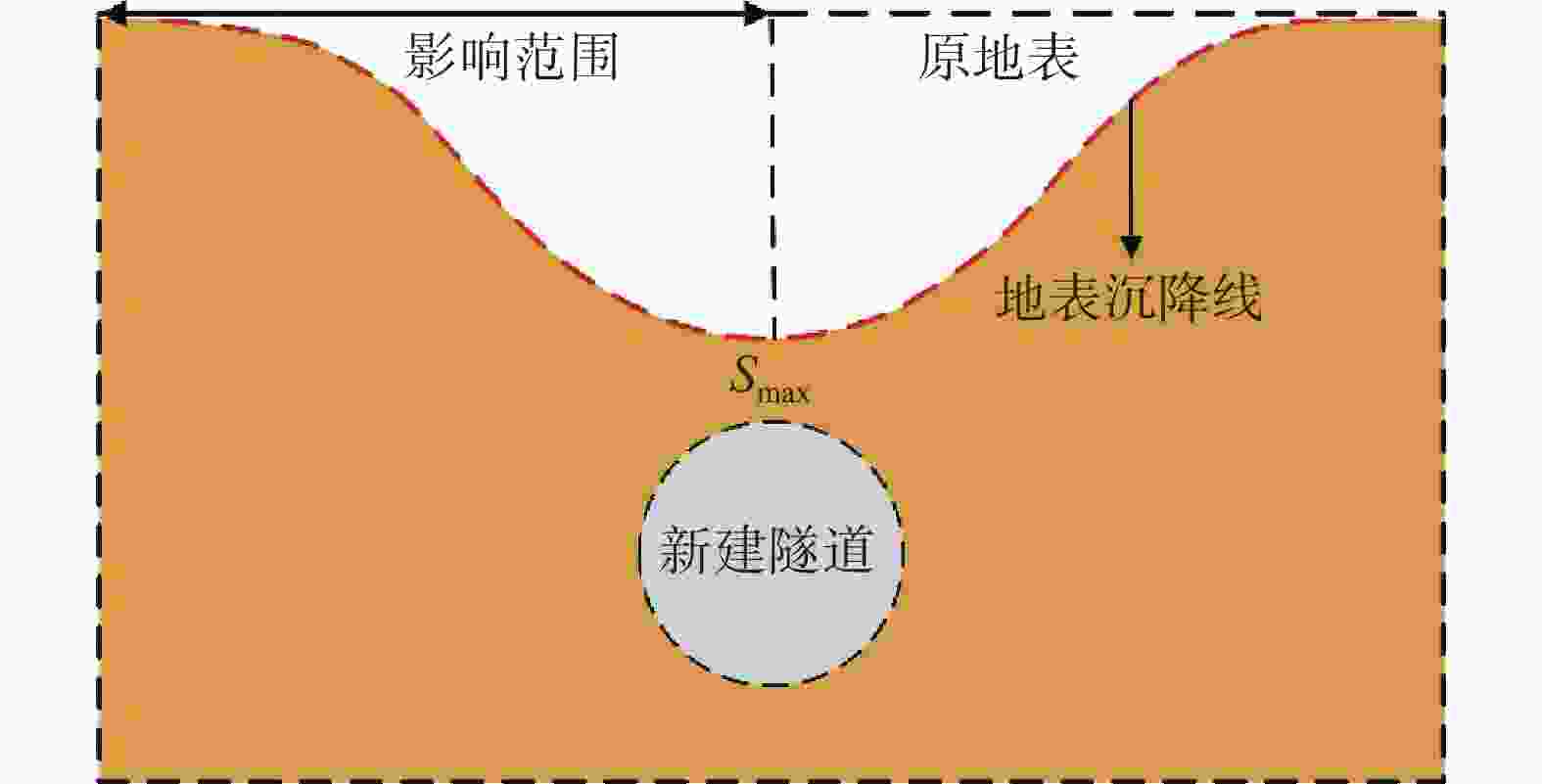
表 1 Peck公式中最大沉降值Smax研究
文献 公式 [12] $ S_{\max}=\dfrac{V_{\mathrm{s}}}{i\sqrt{2\text{π}}}=\dfrac{V_1D^2}{0.313i} $ [13] $ S_{\max }=\dfrac{t}{(a+b t)} $ [14] $ S_{\text {max }}= \begin{cases}(0.4 \% \sim 1 \%) R & 4 R \leq z_0<20 R \\ (1 \% \sim 1.6 \%) R & z_0<4 R\end{cases}$ [15] $ S_{\max }=\dfrac{(1+\kappa) V_{0}}{i \sqrt{2 {\text{π}}}} $ [16] $ S_{\max }(z)=S_{\max }\left(1-\dfrac{z}{z_{0}}\right)^{-0.3} $ 注:VS为单位长度沉降槽体积;V1为地层损失率;D为隧道等效外径;V0为地层损失量;κ为体积变化量与地层损失量的比值;t为时间;a,b为参数;R为隧道半径。 表 2 Peck公式中沉降槽宽度系数i
文献 公式 [16] $ i(z)=i\left(1-\dfrac{z}{z_{0}}\right)^{-a .3} $ [17] $ \bar{i}=\left\{\begin{array}{ll}0.43 z_{0}+1.1 & \text { 黏土 } \\0.28 z_{0}-0.1 & \text { 粒土 }\end{array}\right. $ [18] $ \tilde{I}=K\left(z_{0}-z\right) $ [19] $ i=-\sqrt{1 / 2 k} $ [20] $ \dot{I}=-0.25 \ln \left(z_{0}-z\right)+1.234 $ 注:K为沉降相关参数;z0为隧道埋深;z为研究地层深度;k为拟合参数。 表 3 地表截面沉降相关数据Peck拟合参数
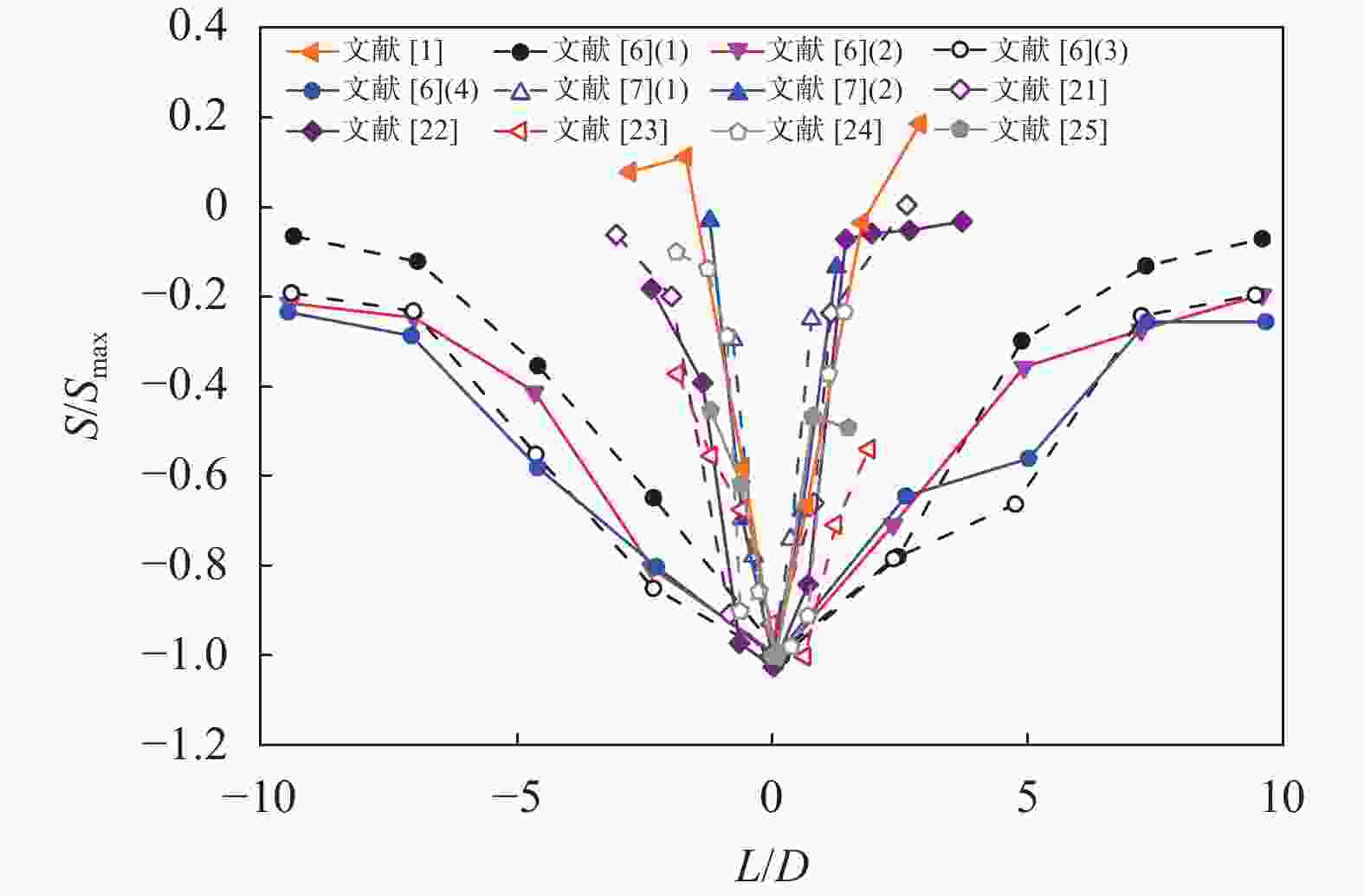
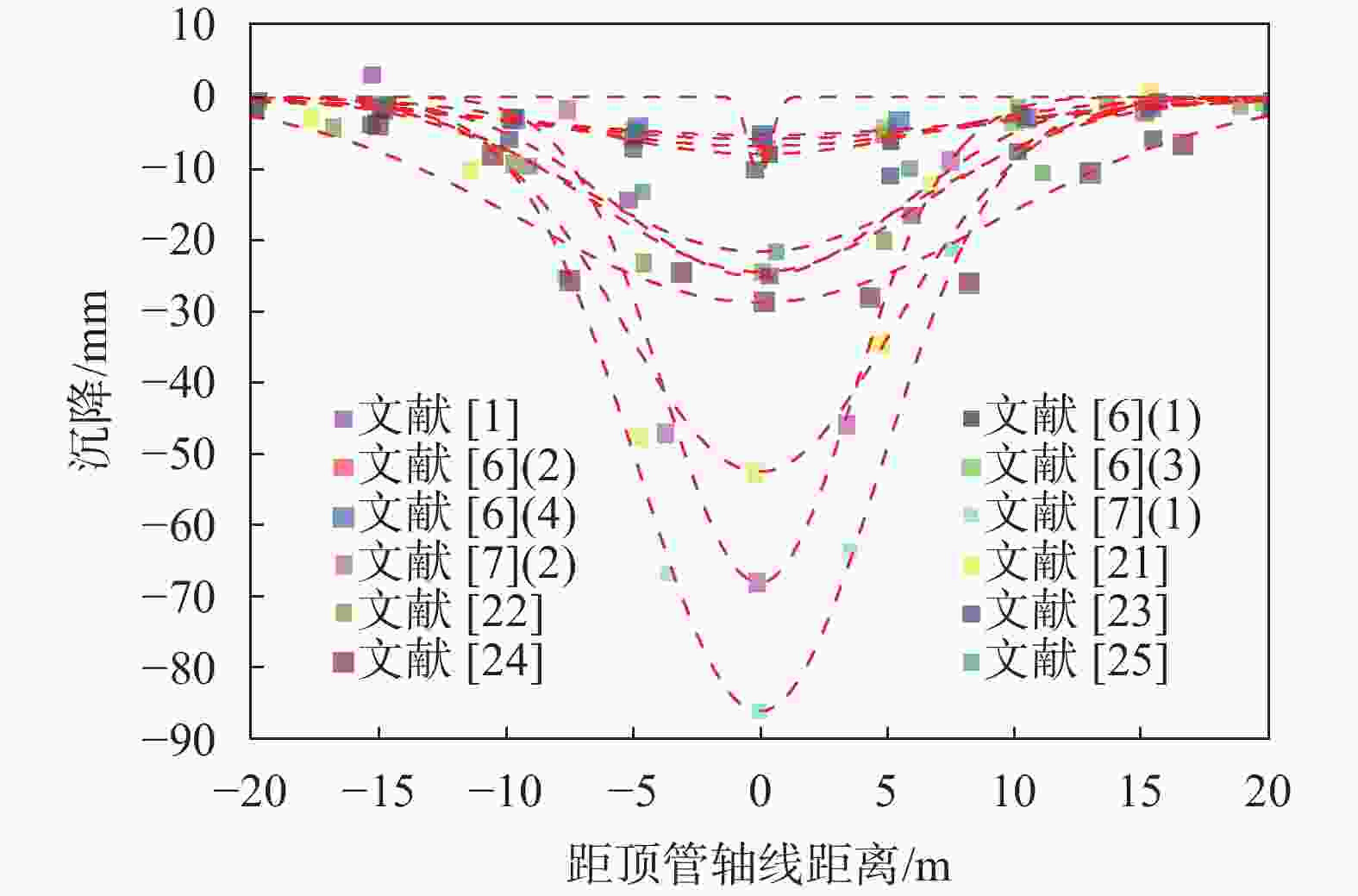
文献 D/m Smax/mm i/mm R2 L0/m L0/D [1] 10.0 −25.20 5.57 0.941 14.14 1.4 [6] 2.1 −8.05 6.68 0.973 13.65 6.5 2.1 −6.89 8.21 0.872 16.11 7.7 2.1 −5.93 9.36 0.896 17.65 8.4 2.1 −5.38 9.66 0.860 17.71 8.4 [7] 10.0 −86.00 4.74 0.993 14.15 1.4 6.1 −68.00 3.73 0.975 10.83 1.8 [21] 6.5 −52.50 5.35 0.879 15.2 2.3 [22] 8.0 −24.53 6.41 0.919 16.2 2.0 [23] 9.2 −11.18 失败 [24] 13.3 −28.70 9.19 0.862 23.8 1.8 [25] 8.5 −21.70 6.84 0.356 16.9 2.0 表 4 既有隧道上浮数据Peck拟合参数
表 5 土层物理力学参数
地层 ρ w E0 υ φ c K0 n 素填土 1.96 32 5 0.25 10 15 0.34 0.48 黏土 1.92 27.3 20 0.28 11.5 50 0.37 0.44 粉土 1.97 21.8 10 0.30 25 3 0.43 0.40 圆砾 2.08 25 0.25 35 0 0.33 泥岩 2.1 17 20 0.35 18 65 0.27 0.01 表中:ρ为天然密度,g/cm3;w为天然含水率,%;E0为变形模量,MPa;υ为泊松比;φ为内摩擦角,(°);c为黏聚力,kPa;K0为静止侧压力系数;n为孔隙率。 -
[1] 佘芳涛, 吴征奇, 周伟踪, 等. 考虑关键施工参数的矩形顶管隧道围岩变形控制分析[J]. 岩土工程学报,2022,44(S1):247-253. doi: 10.11779/CJGE2022S1044 [2] 朱 剑, 李振勇, 张 泷. 复杂环境下大断面矩形顶管法施工过程地表沉降规律及控制措施研究[J]. 岩土工程技术,2017,31(1):49-54. doi: 10.3969/j.issn.1007-2993.2017.01.012 [3] 丁传松. 大断面矩形顶管下穿合流污水箱涵变形分析[J]. 岩土工程技术,2023,37(1):1-6. doi: 10.3969/j.issn.1007-2993.2023.01.001 [4] 魏 纲, 徐日庆, 屠 玮. 顶管施工引起的土体扰动理论分析及试验研究[J]. 岩石力学与工程学报,2004(3):476-482. doi: 10.3321/j.issn:1000-6915.2004.03.022 [5] 郑 跃, 丁文其, 陈立生. 受顶管施工影响的土体扰动分析与实测研究[J]. 地下空间与工程学报,2010,6(5):1015-1020. doi: 10.3969/j.issn.1673-0836.2010.05.024 [6] 刘浩航. 顶管上穿施工对既有地铁隧道的影响分析[D]. 湘潭: 湘潭大学, 2014. [7] 李明宇, 王 松, 张维熙, 等. 大断面矩形顶管隧道施工引起的地面沉降分析[J]. 铁道建筑,2019,59(5):81-84. doi: 10.3969/j.issn.1003-1995.2019.05.19 [8] 吴垠龙, 刘 维, 贾鹏蛟, 等. 矩形顶管近距离上穿既有隧道施工扰动分析[J]. 地下空间与工程学报,2022,18(6):1968-1978. [9] 徐 新, 付江山, 吴晓斌, 等. 矩形顶管施工引起的地表沉降研究[J]. 公路工程,2017,42(4):4-9. doi: 10.3969/j.issn.1674-0610.2017.04.002 [10] 魏 纲, 吴华君, 陈春来. 顶管施工中土体损失引起的沉降预测[J]. 岩土力学,2007(2):359-363. doi: 10.3969/j.issn.1000-7598.2007.02.030 [11] PECK R B. Deep excavations and tunneling in soft ground[C]//7th International Conference on Soil Mechanics and foundation Engineering. Mexico City, 1969: 225-290. [12] ATTEWELL P B, YEATES J, SELBY A R. Soil movements induced by tunnelling and their effects on pipelines and structures[M]. Glasgow: lackie, 1986: 10-50. [13] FANG Y S, LIN L S J, LIN L J S. Time and settlement in EPB shield tunnelling[J]. Tunnels & Tunnelling,1993,25(11):27-28. [14] 方从启, 王承德. 顶管施工中的地面沉降及其估算[J]. 江苏理工大学学报,1998(4):108-112. [15] 房营光, 莫海鸿, 张传英. 顶管施工扰动区土体变形的理论与实测分析[J]. 岩石力学与工程学报,2003(4):601-605. doi: 10.3321/j.issn:1000-6915.2003.04.018 [16] 姜忻良, 赵志民, 李 园. 隧道开挖引起土层沉降槽曲线形态的分析与计算[J]. 岩土力学,2004(10):1542-1544. doi: 10.3969/j.issn.1000-7598.2004.10.006 [17] O'REILLY M P, NEW B M. Settlements above tunnels in the United Kingdom-their magnitude and prediction[M]. 1982. [18] MAIR R J, TAYLOR R N, BRACEGIRDLE A. Subsurface settlement profiles above tunnels in clays[J]. Geotechnique,1993,43(2):315-320. doi: 10.1680/geot.1993.43.2.315 [19] 韩 煊, 罗文林, 李 宁. 地铁隧道施工引起沉降槽宽度的影响因素[J]. 地下空间与工程学报,2009,5(6):1188-1193,1219. doi: 10.3969/j.issn.1673-0836.2009.06.023 [20] JONES B D. Low-volume-loss tunnelling for London ring main extension[J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering,2010,163(3):167-185. doi: 10.1680/geng.2010.163.3.167 [21] 董 俊. 地铁过街通道矩形顶管施工变形监测分析[J]. 铁道工程学报,2016,33(8):106-110. doi: 10.3969/j.issn.1006-2106.2016.08.021 [22] 郑知斌, 李名淦, 闫朝涛, 等. 北京首条矩形顶管风险防控设计与沉降分析[J]. 地下空间与工程学报,2021,17(4):1281-1290. [23] 赵玉权. 深圳地铁10号线大断面矩形顶管施工控制技术研究[D]. 北京: 北京交通大学, 2021. [24] 王发民, 孟庆军, 张 浩, 等. 浅埋富水地层特大断面矩形顶管隧道掘进参数分析[J]. 隧道建设(中英文),2023,43(2):316-326. [25] 王蕴晨. 并行超大浅埋矩形顶管力学特性研究及工程应用[D]. 福州: 福建工程学院, 2020. [26] 张 振. 超大矩形断面顶管隧洞开挖引起的地表沉降研究[D]. 郑州: 华北水利水电大学, 2016. [27] 陈 杰. 四孔并行矩形顶管施工力学效应研究[D]. 成都: 西南交通大学, 2015. [28] 郑 斌. 大断面类矩形顶管壳体土压及顶进阻力分析——以上海淞沪路—三门路下立交工程为例[J]. 隧道建设(中英文),2021,41(10):1740-1747. [29] 韩占波, 豆小天, 曹伟明, 等. 浅覆土小间距矩形顶管施工地表变形控制技术[J]. 隧道建设(中英文),2019,39(3):496-503. [30] 叶耀东. 大断面矩形顶管近距离上穿地铁隧道变形控制探讨[J]. 城市道桥与防洪,2015(7):19,203-205. doi: 10.3969/j.issn.1009-7716.2015.07.062 [31] 张志伟, 梁荣柱, 高 坤, 等. 考虑管片环间接头弱化的新建隧道上穿引起既有盾构隧道纵向变形分析[J]. 岩石力学与工程学报,2022,41(S1):2955-2970. [32] 李志南, 潘 珂, 王位赢. 并行顶管近距离上穿既有盾构隧道的安全分析[J]. 地下空间与工程学报,2020,16(S2):939-944,975. [33] 石 雷, 吴 宇, 殷茜东. 矩形顶管上穿运营隧道的施工参数控制分析[J]. 工程建设,2020,52(7):50-53. -




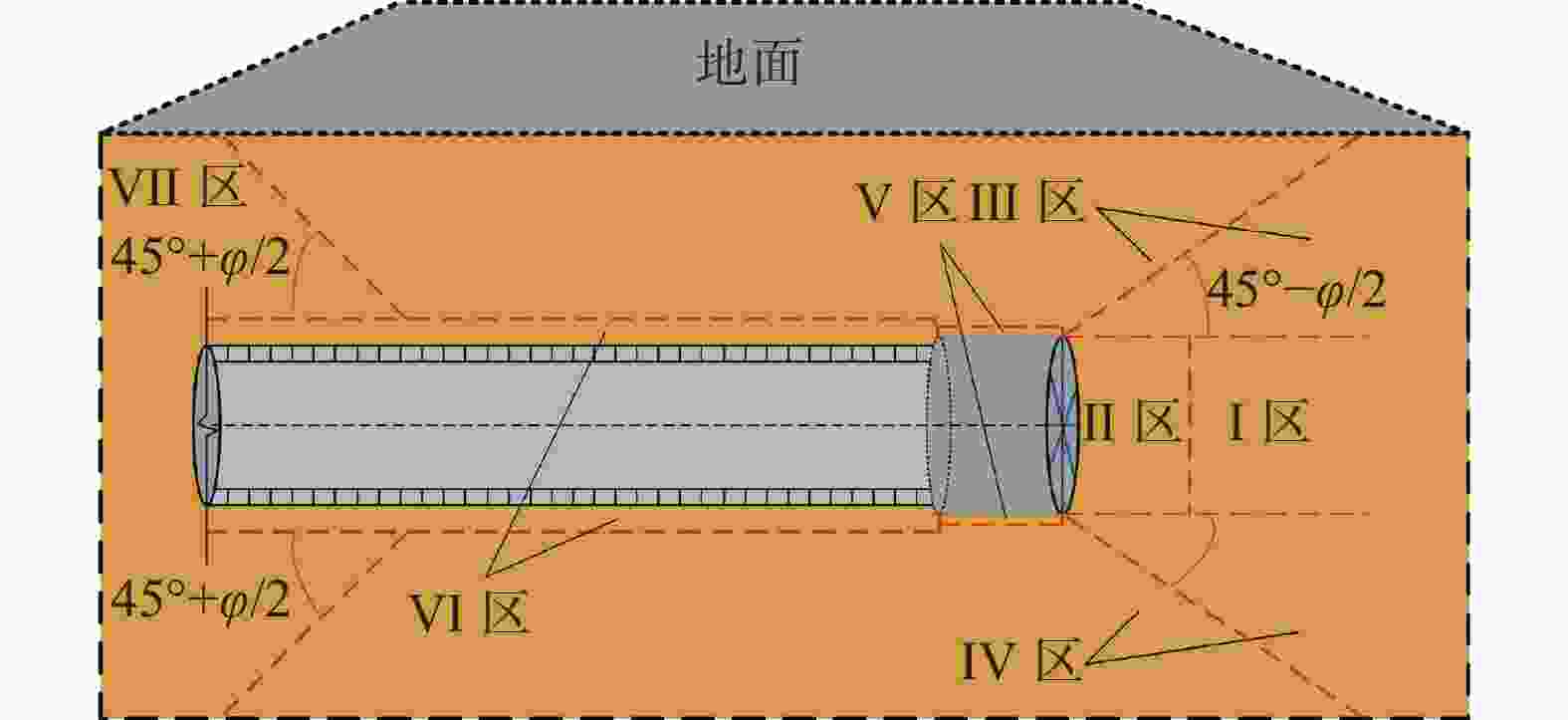
 下载:
下载: