Stability Analysis of a Landslide in Yalong River
-
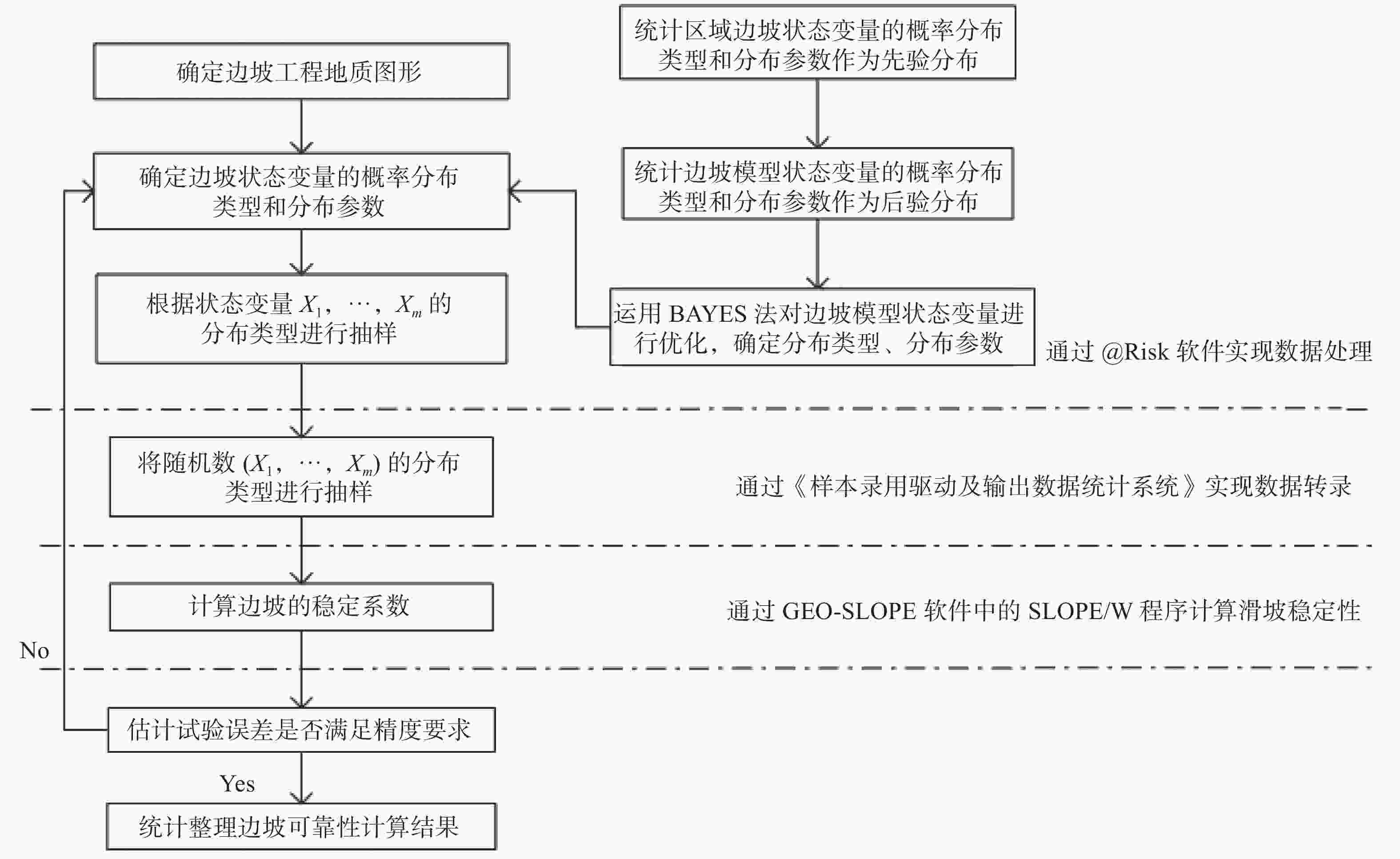
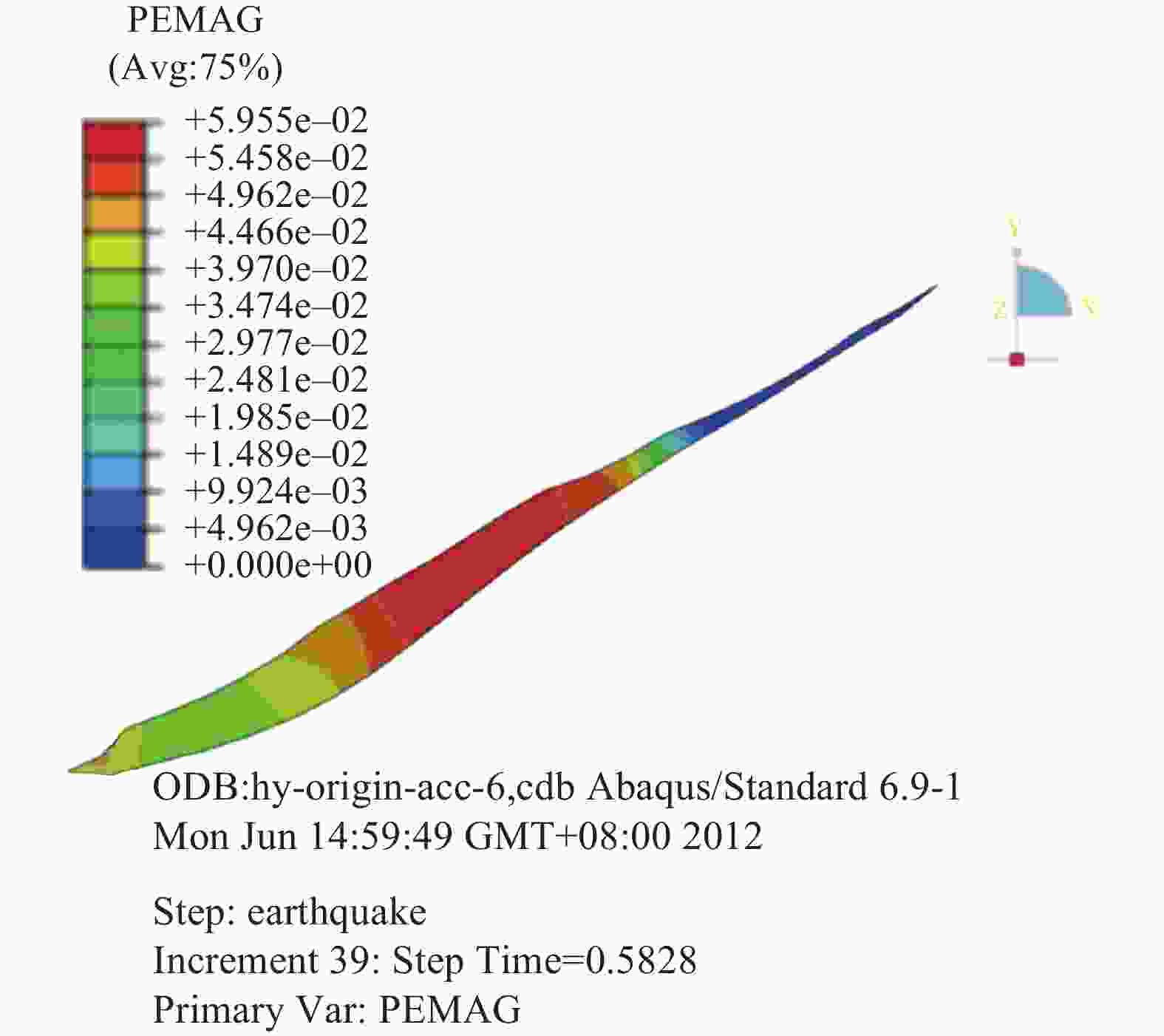
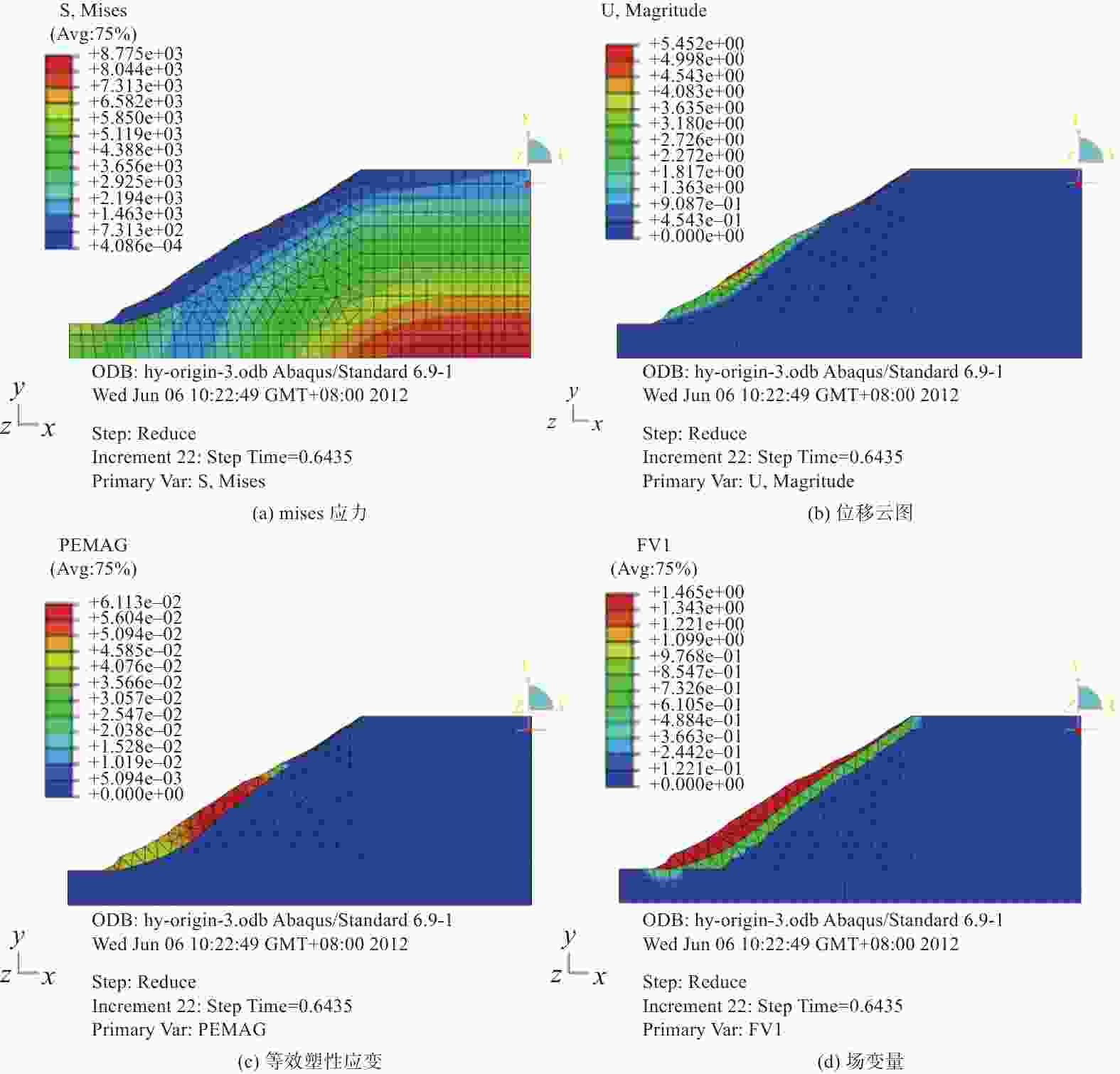
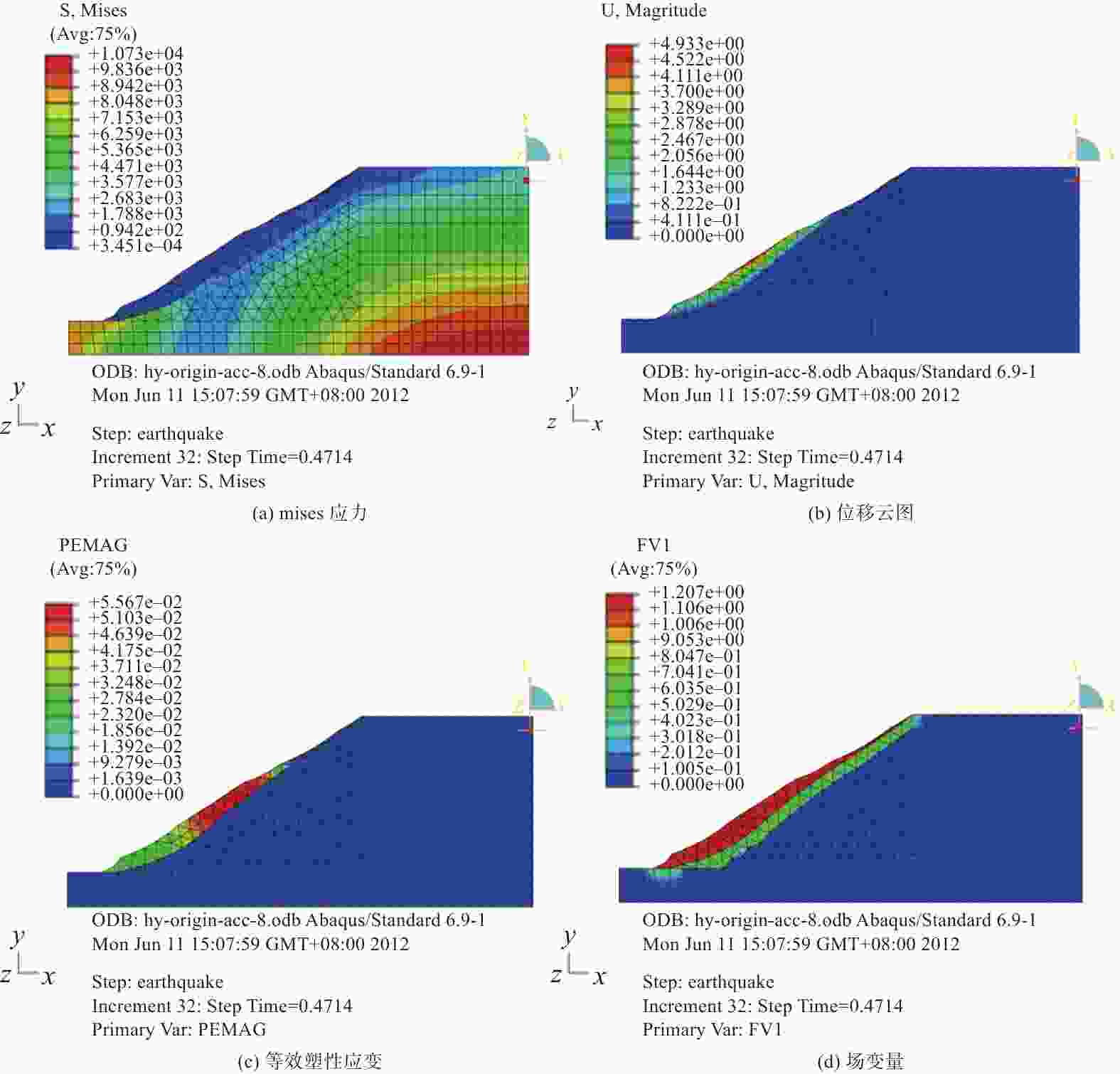
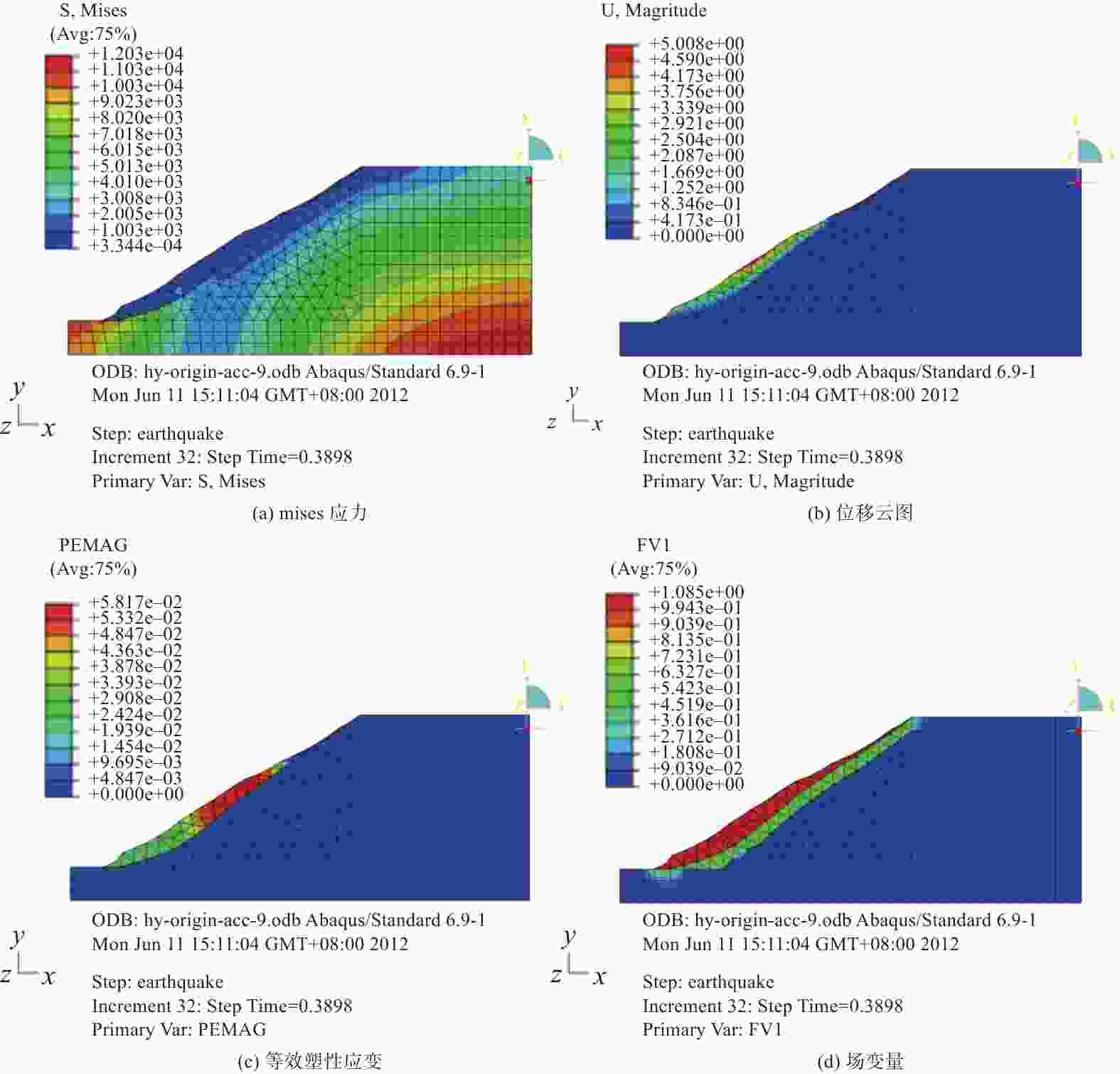
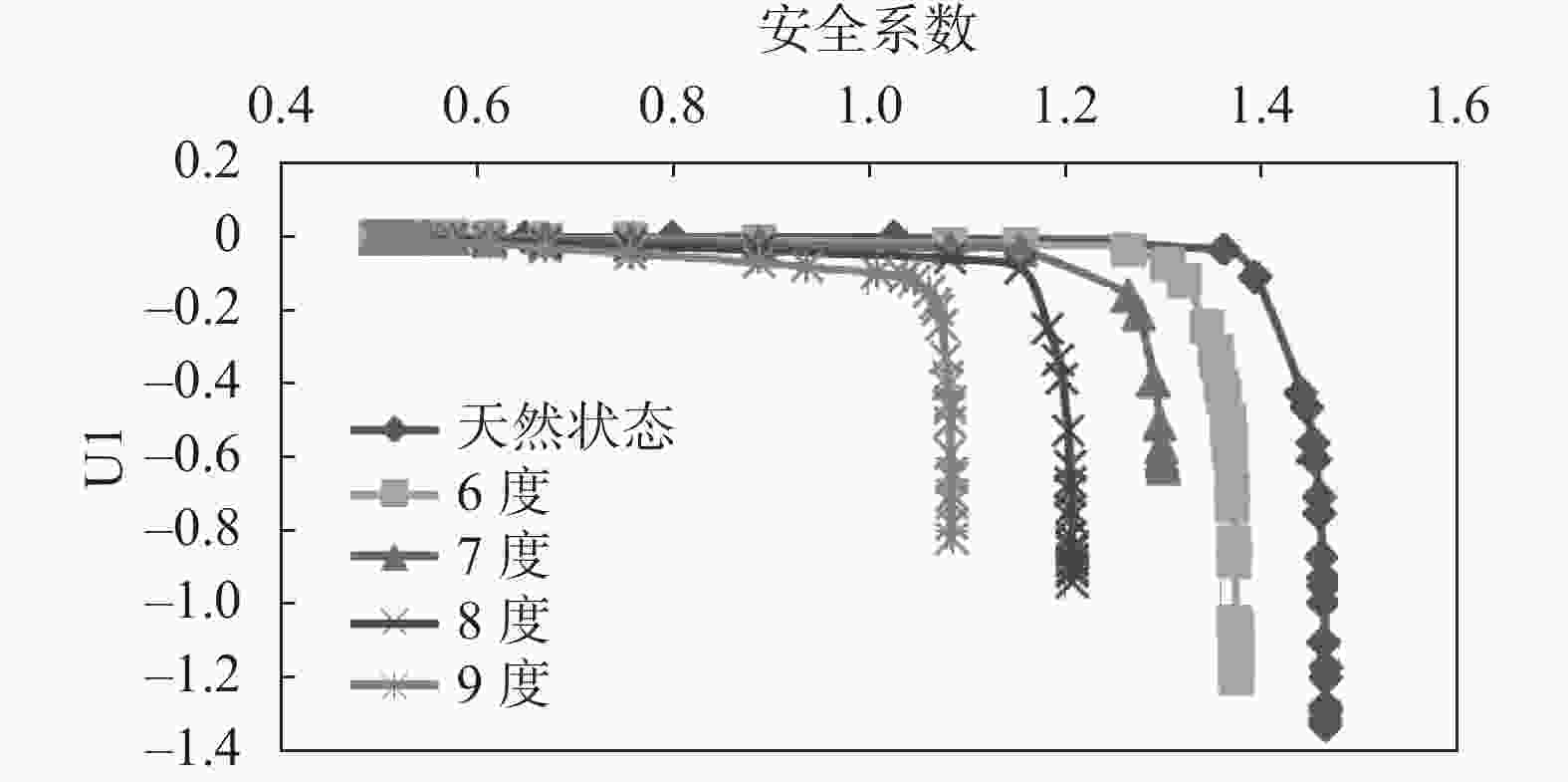
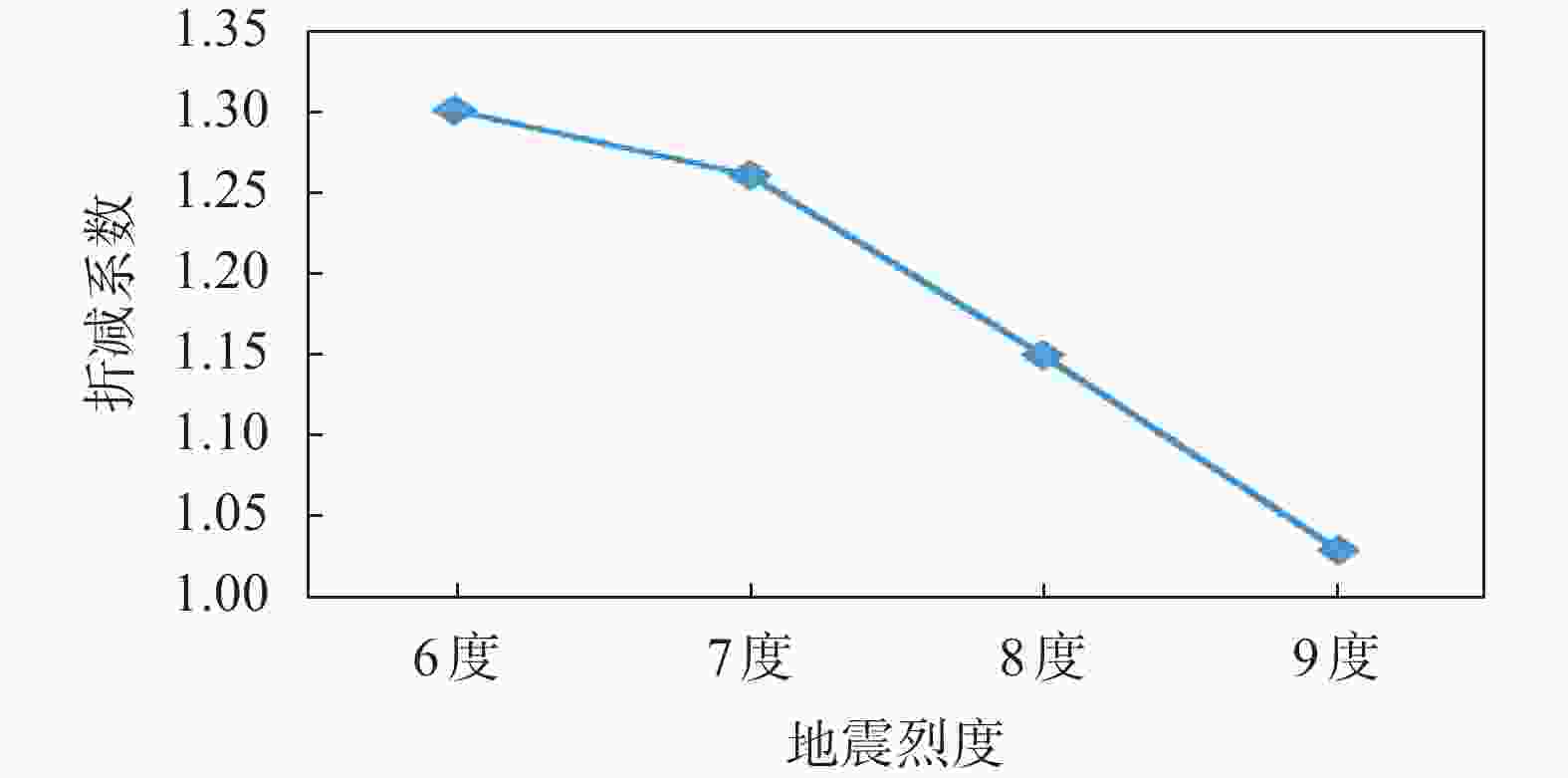
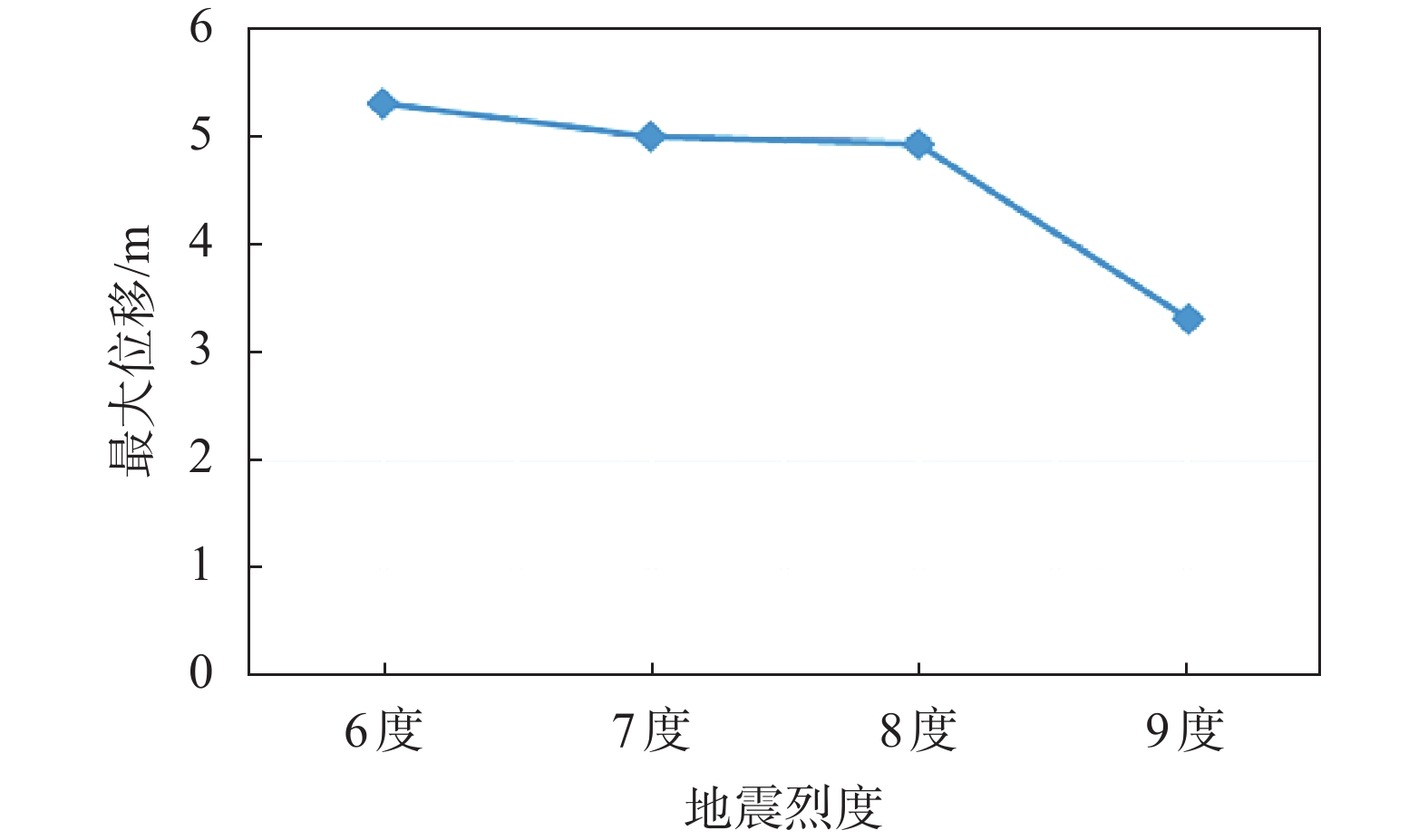
摘要: 为给雅砻江某滑坡灾害风险评估提供可靠依据,分别采用可靠度法和强度折减法对该滑坡体进行稳定性分析。应用GEO-SLOPE软件,运用基于极限平衡理论的可靠度法分析滑坡体的稳定性以及滑坡体在蓄水暴雨工况和蓄水地震工况下的失稳概率;运用有限元强度折减法对各工况进行分析,并通过软件计算分析得到地震烈度和安全系数之间的关系:随着地震烈度的增加,安全系数呈陡降趋势。对于滑坡稳定性分析,两种方法取得了一致性结果,基于极限平衡理论的可靠度法计算方便但有较大的局限性,有限元强度折减法是以弹塑性理论为基础,能直观反映出滑坡的变形位移和破坏过程,更接近于工程实际情况。Abstract: In order to provide a reliable basis for landslide risk assessment, the stability of a typical landslide body was calculated and analyzed. Two different methods were used, compared and analyzed, including reliability method and strength reduction method. With the help of GEO-SLOPE software and the method of limit equilibrium theory, the stability of the landslide body was analyzed. The probability of instability of the landslide occurs under two conditions: water storage and heavy rain, water storage and earthquake. The finite element strength reduction method was used to analyze each working condition, and the relationship between seismic intensity and safety coefficient was obtained through software calculation and analysis. With the increase of seismic intensity, the safety coefficient decreases rapidly. It is convenient to calculate through limit equilibrium method but has great limitation. The finite element strength reduction method is based on the elastic-plastic theory, which can directly reflect the deformation, displacement and failure process of the landslide. This method is closer to the actual engineering situation.
-
Key words:
- landslide /
- stability /
- reliability /
- strength reduction /
- safety factor
-
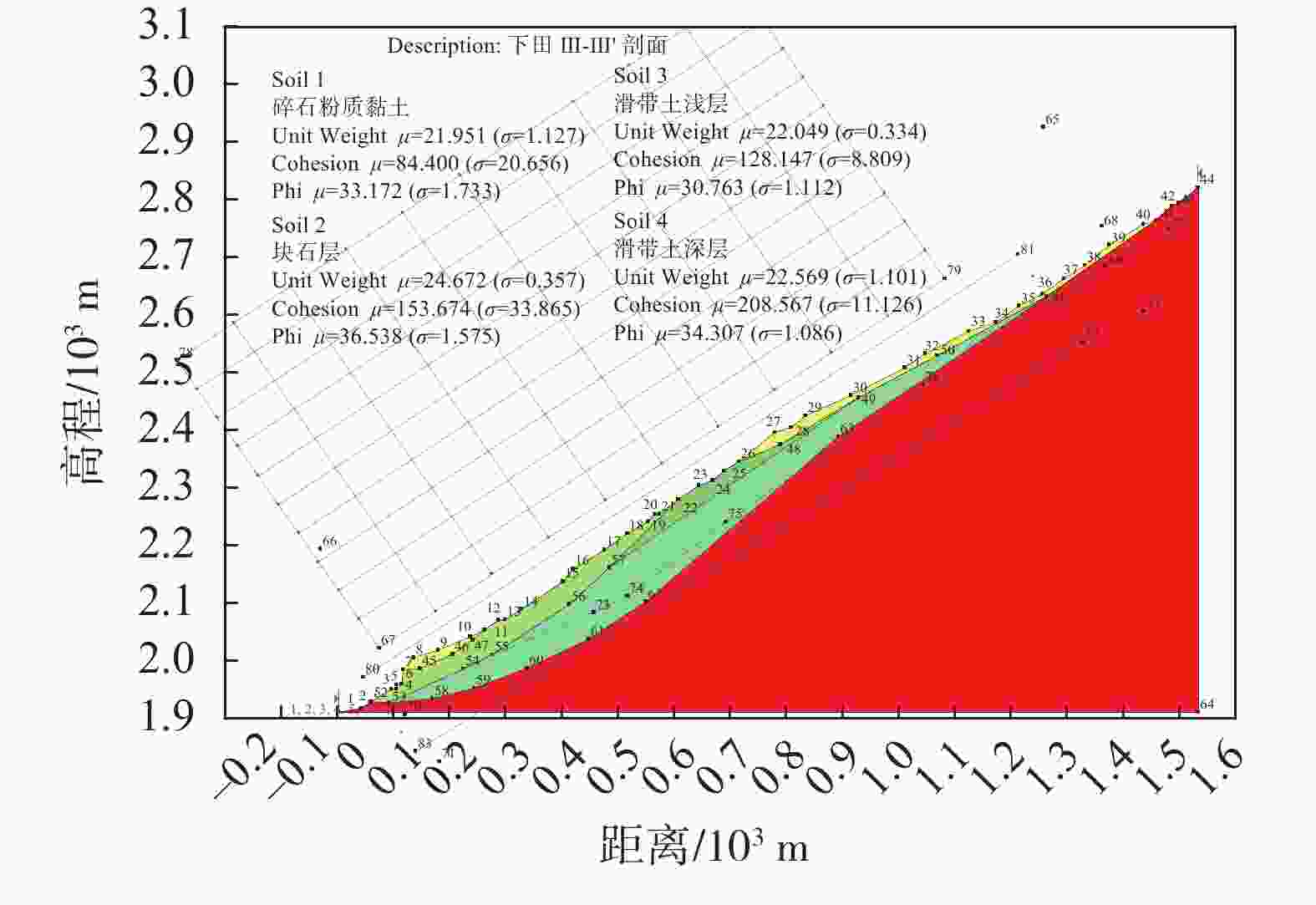
表 1 下田滑坡体A区Ⅲ-Ⅲ′剖面稳定性计算结果
计算工况 计算方法 安全系数 失稳概率/% 安全系数分布/% 均值 方差 >1 >1.05 >1.1 >1.15 工况1天然 Bishop法 1.3426 0.04272 0 100 100 100 100 M-P法 1.3392 0.03542 0 100 100 100 100 工况2正常蓄水 Bishop法 1.3074 0.07012 0 100 100 100 100 M-P法 1.2995 0.07092 0 100 100 100 100 工况3暴雨 Bishop法 1.2636 0.04312 0 100 99.82 99.45 M-P法 1.2598 0.03872 0 100 99.89 99.71 工况4蓄水暴雨 Bishop法 1.1925 0.06772 0.34 99.66 97.03 86.31 M-P法 1.1907 0.06622 0.37 99.63 97.15 85.89 工况5水位骤降 Bishop法 1.1632 0.04232 0 100 100 99.41 M-P法 1.1651 0.04202 0 100 100 99.33 工况6地震 Bishop法 1.1207 0.03852 0 100 96.20 M-P法 1.1145 0.03832 0 100 95.71 工况7蓄水地震 Bishop法 1.0852 0.04022 7.63 92.47 77.50 M-P法 1.0866 0.03942 7.10 92.90 79.23 表 2 不同地震烈度所对应的水平和垂直加速度
地震烈度 水平加速度 垂直加速度 6 度 0.05g 0.033333g 7 度 0.1g 0.066667g 8 度 0.2g 0.133333g 9 度 0.4g 0.266667g 注:重力加速度g为9.8 m/s2。 -
[1] MA J Z,ZHANG J,HUANG H W,et al. Identification of representative slip surfaces for reliability analysis of soil slopes based on shear strength reduction[J]. Computers and Geotechnics,2017,85:199-206. doi: 10.1016/j.compgeo.2016.12.033 [2] GRIFFITHS D V,LANE P A. Slope stability analysis by finite elements[J]. Geotechnique,1999,49(3):387-403. doi: 10.1680/geot.1999.49.3.387 [3] DUNCAN J M. State of the art: limit equilibrium and finite-element analysis of slopes[J]. Journal of Geotechnical Engineering,1996,22(7):577-596. [4] 陈祖煜,弥宏亮,汪小刚. 边坡稳定三维分析的极限平衡方法[J]. 岩土工程学报,2001,23(5):525-529. doi: 10.3321/j.issn:1000-4548.2001.05.001 [5] 陈祖煜,徐佳成,孙 平,等. 重力坝抗滑稳定可靠度分析: (一)相对安全率方法[J]. 水力发电学报,2012,31(3):148-159. [6] 李世海,刘天苹,刘晓宇. 论滑坡稳定性分析方法[J]. 岩土工程学报,2000,28(S2):3309-3324. [7] 刘 宁,贾 超,陈 进. 基于可靠度的工程风险决策初探[J]. 岩土力学,2004,25(8):1297-1301. [8] 蒋水华,祁小辉,曹子君,等. 基于随机响应面法的边坡系统可靠度分析[J]. 岩土力学,2015,36(3):809-818. [9] 曾 鹏,陈 语,李天斌. 基于拟牛顿近似二阶法的岩土工程系统可靠性分析[J]. 岩石力学与工程学报,2018,37(3):726-733. [10] HUANG H W,WEN S C,ZHANG J,et al. Reliability analysis of slope stability under seismic condition during a given exposure time[J]. Landslides,2018,15(11):2303-2313. doi: 10.1007/s10346-018-1050-9 [11] ZHANG L L, LI J H, LI X, et al. Rainfall-induced soil slope failure: Stability analysis and probabilistic assessment[M]. CRC Press, 2018. [12] GAI F,UGAI K. Numerical analysis of the stability of a slope reinforced with piles[J]. Soils and Foundations,2000,40(1):73-84. doi: 10.3208/sandf.40.73 [13] WON J,YOU K,JEONG S,et al. Coupled effects in stability analysis of pile-slope system[J]. Computers and Geotechnics,2005,32(4):304-315. doi: 10.1016/j.compgeo.2005.02.006 [14] Itasca Consulting Group. FLAC3D: Fast Lagrangian Analysis of Continua in Three-Dimensions [M]. Ver. 7.0. Minneapolis: Itasca, 2019. [15] 郑颖人,赵尚毅,邓楚键,等. 有限元极限分析法发展及其在岩土工程中的应用[J]. 中国工程科学,2006,12(8):39-61. doi: 10.3969/j.issn.1009-1742.2006.08.008 [16] 李 强,管长生,周 武. 基于 Monte-carlo 法的滑坡稳定可靠性分析[J]. 岩石力学与工程学报,2001,(S1):1674-1676. [17] 赵 辉,谭跃虎,徐 辉,等. 雅砻江上田边坡可靠性蒙特卡洛方法综合运用[J]. 地下空间与工程学报,2010,6(5):938-945. [18] 杜 聪. 基于ABAQUS强度折减法的边坡稳定性分析[J]. 交通科学与工程,2018,34(2):31-34. [19] 吴 标, 王志斌, 安永林, 等. 强度折减法在建筑边坡稳定性分析中的应用[J], 土工基础, 2016, 30(4): 461-463. -





 下载:
下载: